1. Аналіз стійкості лінійних безперервних стаціонарних систем

Найбільш загальним|спільним| методом аналізу лінійних систем є|з'являються| дослідження диференційних рівнянь

,

які характеризують динаміку процесів, що відбуваються|походять| в системі .

Повне|цілковите| рішення диференційного рівняння складається з двох частин|часток|:

,

де - загальне|спільне| рішення одного диференційного рівняння, що відповідає вільному руху системи і залежить від властивостей системи; - часткове рішення неоднорідного диференційного рівняння, що відповідає вимушеному|змушеному| сталому режиму системи під дією зовнішніх впливів |збурень| і залежить як від властивостей системи, так і від зовнішніх дій .

Однією з основних характеристик системи, що визначають її працездатність, є стійкість, під якою розуміють властивість системи повертатися до стану сталої рівноваги після усунення впливу, що порушив вказану рівновагу. Нестійка система не повертається до стану рівноваги, а безперервно віддаляється від нього або здійснює неприпустимо великі коливання [3;4] .

Математична форма запису умови стійкості представляє собою вимоги перетворення на нуль при необмеженому зростанні часу з моменту початку перехідного процесу:

.

Показано, що необхідна і достатня умова стійкості системи полягає в тому, щоб|аби| всі корені характеристичного рівняння

мали від’ємну|заперечну| реальну частину|частку|, тобто лежали в лівій напівплощині комплексної змінної р.

На практиці застосовують спеціальні методи, що дозволяють, не вдаючись до вирішення диференційного або характеристичного рівняння, а іноді|інколи| навіть і до складання цих рівнянь, робити|чинити| висновки про стійкість лінійної системи. Такі методи називають критеріями стійкості.

1. Критерій стійкості Гурвиця.

Перевірка стійкості за крітерієм Гурвиця зводиться до обчислення|підрахунку| по коефіцієнтах характеристичного рівняння так званих визначників Гурвиця , які для стійкої системи при додатньому коефіцієнті мають бути додатні:

.

Система буде знаходитися|перебуватиме| на межі|кордоні| стійкості, якщо . Нехай|нехай| структурна схема замкненої системи автоматичного регулювання (САР) має вигляд|вид|, показаний на рис.1.1, де 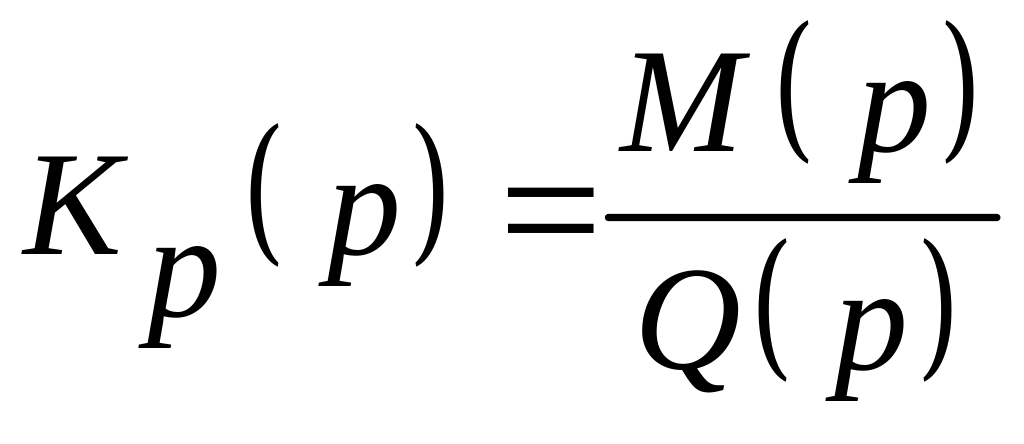- передаточна функція розімкненої системи. Тоді передаточна функція замкненої системи і характеристичний поліном замкненої системи визначаються з|із| виразів

.

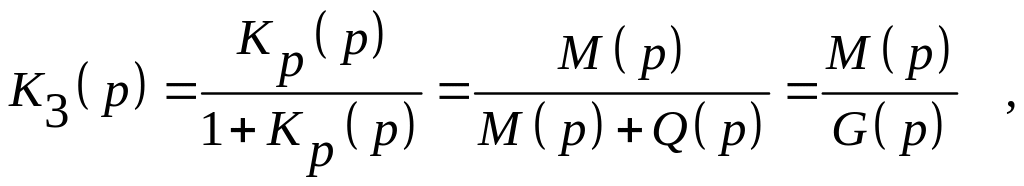
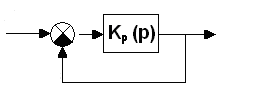
Рис.1.1

Для отримання визначників Гурвиця складається матриця з|із| коефіцієнтів , на головній діагоналі якої в порядку убування починаючи|розпочинати| з|із| , виписуються коефіцієнти характеристичного полінома від до ; справа від головної діагоналі записуються|занотовують| коефіцієнти із|із| зростаючими індексами, зліва|ліворуч| – з|із| тими, що убувають. Всі коефіцієнти , з індексами менше нуля і більше n замінюються нулями.

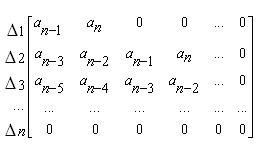
(1.1)

Відкреслюючи відповідні рядки і стовпці матриці, отримуємо|одержуємо| визначники Гурвиця:

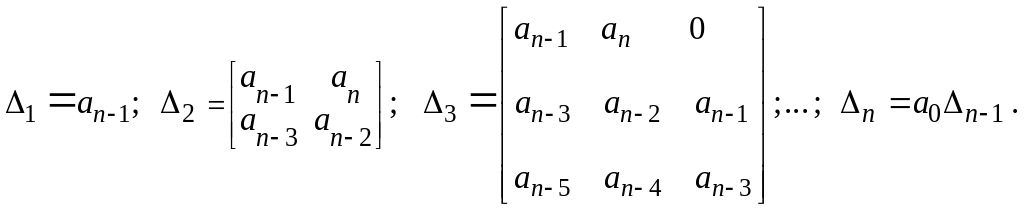(1.2)

Можна показати, що необхідною (але|та| не достатньою) умовою стійкості є|з'являється| додатність всіх коефіцієнтів характеристичного рівняння, тобто , , … , .

Для систем, що описуються характеристичним поліномом першого і другого порядків|ладів|, необхідна умова стійкості є|з'являється| одночасно і достатньою, а для вищих порядків|ладів| поліномів потрібні додаткові співвідношення між коефіцієнтами .

Наприклад, для полінома третього порядку|ладу| необхідно, щоб|аби| .