Смысл критериев различия

Некоторые результаты выборочной статистической совокупности могут далеко отстоять от среднего значения, тогда возникает со­мнение, является ли это результатом маловероятных, но все же воз­можных больших отклонений от центра соответствующей генераль­ной совокупности, или же результатом того, что в рассматривае­мую выборку почему-то оказались включенными результаты, принадлежащие в действительности к другой генеральной совокуп­ности, и являются ли данные эмпирические совокупности выбор­ками из одной и той же генеральной совокупности? Для этой цели применяется нулевая гипо­теза.

Нулевая гипо­теза состоит в том, что данные эмпирические совокупности явля­ются выборками из одной и той же генеральной совокупности, если между генеральными совокупностями, выборками из ко­торых являются данные эмпирические совокупности, нет реального различия.

Правильность нулевой гипотезы можно проверить следующим образом. Предположив справедливость нулевой гипотезы, т. е. от­сутствие реального различия, мы вычисляем вероятность того, что из-за случайности выборки расхождение может достигнуть факти­чески наблюденной величины; если эта вероятность окажется очень малой, то нулевая гипотеза отвергается (т. е. маловероятно, что расхождение вызвано случайными причинами, а не реальным раз­личием). Вероятность Р, которую принимают за основу при стати­стической оценке гипотезы, определяет уровень значимости.

Уровень значимости характеризует, в какой мере мы рискуем ошибиться, отвергая нулевую гипотезу. Этот выбор в значительной степени определяется конкретными задачами исследования. Для практических приложений вполне пригоден 5%-ный уровень значимости (95% доверительная вероятность), т. е. принимая этот уровень, мы должны отвергнуть на самом деле вер­ную нуль-гипотезу в 5% всех случаев применения критерия значи­мости. Чем меньше уровень значимости, тем меньше вероятность отвергнуть проверяемую гипотезу.

Доверительный интервал. Критерий Стьюдента

При обработке данных вычисляют приближенные значения не­известных величин, кото-рые в математической статистике называ­ются оценками. Например, среднее значение , по-лученное по дан­ным выборки, представляет собой оценку неизвестного математи­ческого ожидания μ. Поэтому необходимо установить границы, в пределах которых с заданной ве-роятностью можно ожидать по­явления истинного значения определяемой величины.

Чтобы дать представление о точности и надежности оценки μ в математической ста-тистике пользуются так называемыми дове­рительными интервалами.

При больших n выборочные средние распределены прибли­женно нормально вокруг μ со стандартным отклонением Из рассмотрения кривой нормального распределения мы получаем, что около 68,3% всех выборочных находятся в пределах μ± .

Вероятность 68,3% того, что интервал ( — , + ) содер­жит μ, сравнительно невысока. С большей уверенностью можно ут­верждать, что μ покрывается интервалом ( —2 , +2 ), так как вероятность этого равна 95,5%; в том, что μ содержится в ин­тервале ( —3 , +3 ) можно быть почти уверенным: веро­ятность этого равна 99,7%.

Чем выше требование к вероятности вывода об интервале, со­держащем μ, тем шире должен быть интервал, который может обеспечить такую вероятность.

Относительное отклонение выборочного среднего от генераль­ного среднего, т. е.

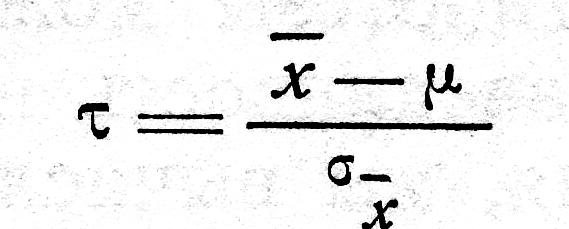
будет оцениваться величиной

.

Если же объемы выборок малы, то распределение величины t отличается от нормального и тем сильнее, чем меньше объем вы­борок. Тогда доля интервалов ( —t , +t ), покрывающих μ, не определяется функцией нормального распределения.

Распределение величин t при разных п (или при разном числе степеней свободы f = п—1) было найдено Стьюдентом. Значения t, обеспечивающие принятый уровень значимости, зависят не только от этого уровня, но и от объема совокупности п (или от числа сте­пеней свободы f). Значения t_Р при соответствующей доверительной вероятности для разных f приводятся в таблицах критерия Стьюдента. Значения t_Р зависят особенно резко от f при малых f. Поэтому увеличение п приводит к сужению доверительного интервала, определяе-

мого величиной

f_Р = t_РS/

не только за счет уменьшения множителя 1/ , но в еще большей степени за счет уменьше-ния t_Р. Так, при Р = 95% изменение п с двух опытов до трех уменьшает множитель t_Р/ с

12,71/ = 9 до 4,3/ =2,5, т. е. доверитель­ный интервал сужается в 3,6 раза. При больших значениях п уве­личение п на единицу сказывается на ширине доверительного ин­тервала гораздо меньше.

На практике часто приходится решать задачу сравнения между собой двух средних результатов. Допустим, что на фабрику поступает сырьё из двух заготовительных пунктов. Каждый пункт опробован и результаты анализа представлены двумя рядами величин:

Необходимо выяснить, есть ли статистически значимая разница в содержании металла в приёмных пунктах. Эту задачу можно решить с помощью критерия Стьюдента, если есть основа­ния полагать, что имеем дело с нормально распределенными на­блюдениями и дисперсии двух систем наблюдений и не отличаются значимо друг от друга.

При выполнении указанных условий для проверки нулевой ги­потезы μ_х —μ_у = 0 вычисляют среднее взвешенное двух дисперсий

(3.19)

и величину

(3.20)

Число степеней свободы здесь f=n₁ + n₂ — 2. Если найденное значение t по абсолютной величине не превосходит табличное зна­чение для 5%-ного уровня значимости, то нуль-гипотеза соблюдается, и она ставится под сомнение, если найденное значение t превосходит табличное для 5%- ного уровня значимости.

В частном случае, когда n₁ = n₂ , выражение упрощается

В описанном выше примере были получены следующие резуль­таты по содержанию металла:

1 пункт

2 пункт

Средневзвешенное двух дисперсий по формуле (3.19)

При f=9 по таблице критерия Стьюдента находим t_0,05 = 2,26.

Таким образом, полученное значение показалось больше таблич­ного и, следовательно, расхождение между содержанием металла в пунктах надо считать значимым.

Если нет основания считать дисперсии равными, то для сравнения двух статистических выборок при n₁ = n₂ можно воспользоваться приближенным t-критерием

с числом степеней свободы

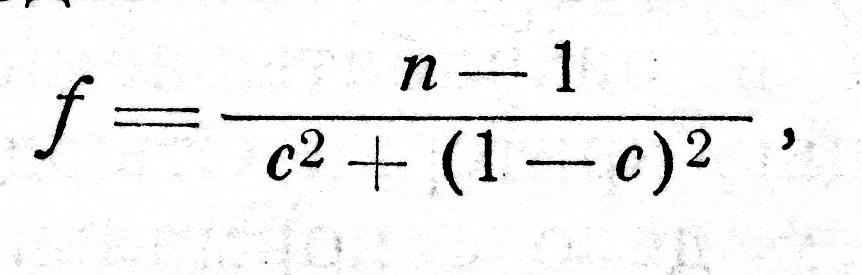
где