ЛЕКЦИЯ 3. (МЛиТА)

АЛГЕБРА ЖЕГАЛКИНА

Определение 1. Множество всех булевых функций с операциями логического умножения и сложения по модулю 2 (исключающее «или») образуют алгебру, которая называется алгеброй Жегалкина.

Часто логическое умножение обозначается так же как и обычное умножение - просто точкой. Отметим свойства операций алгебры Жегалкина.

ТЕОРЕМА 1. Операции алгебры Жегалкина удовлетворяют следующим свойствам:

1. ;

2. ;

3. ;

4. ;

5. ;

6. .

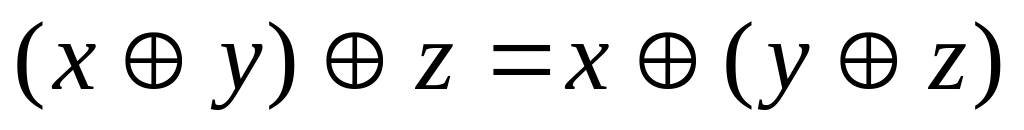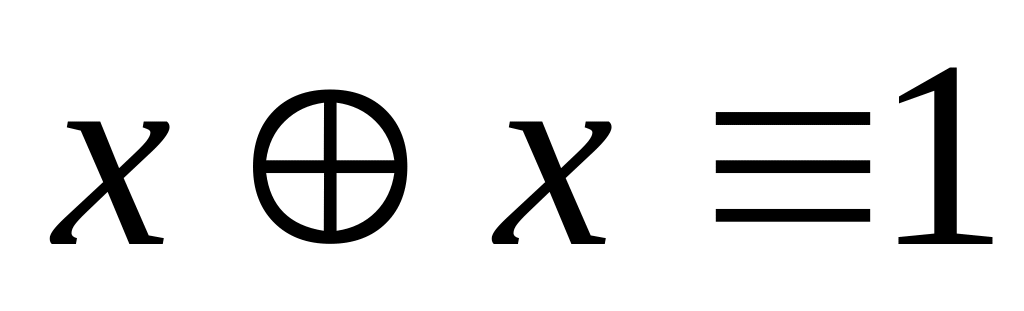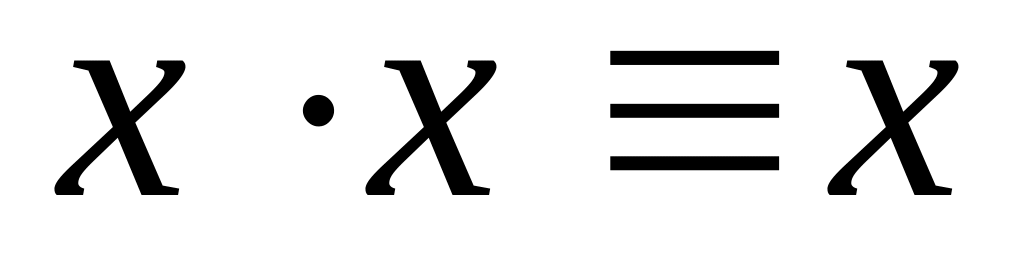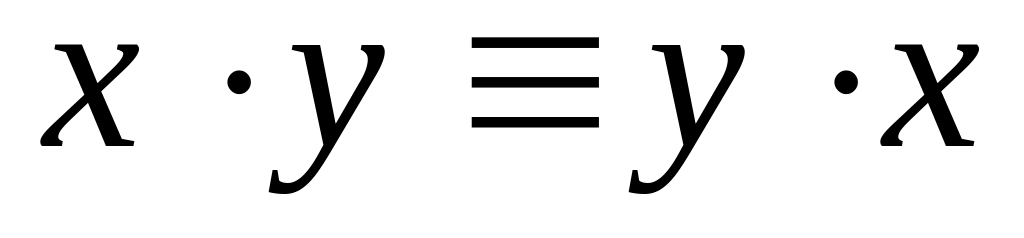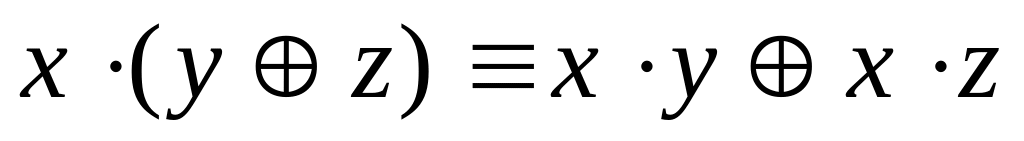Отметим связь операций алгебры Жегалкина с логическими операциями отрицания и дизъюнкции.

ТЕОРЕМА 2. 1) ;

2) ;

3) если формулы А и В несовместны, т.е. , то имеет место равенство .

Доказательство этих теорем можно провести с помощью таблиц истинности или эквивалентными преобразованиями.

Определение 2. Сумма произведений переменных и, быть может, свободного члена 1 называется полиномом Жегалкина.

, где .

ТЕОРЕМА 3. Для каждой булевой функции существует полином Жегалкина , эквивалентный исходной функции.

Доказательство. По булевой функции строим совершенную дизъюнктивную нормальную форму ей эквивалентную . Как известно, элементарные конъюнкции из СДНФ являются несовместными, а потому эта форма будет эквивалентна формуле , где знак суммы означает сложение по модулю 2. Проведя в ней замену в соответствии с теоремой 2 и раскрывая скобки, а затем, приводя подобные в соответствии с теоремой 1, получим искомый полином Жегалкина.

Эту теорему можно усилить.

ТЕОРЕМА 4. Для каждой булевой функции существует единственный полином Жегалкина , эквивалентный исходной функции.

Доказательство. Обозначим через множество всех булевых функций от переменных. Как известно в этом множестве элементов.

Обозначим через множество всех полиномов Жегалкина от переменных. В соответствии с теоремой 3 установлено отображение . Причем это отображение является отображением на всё множество , т.к. сам полином Жегалкина тоже является булевой функцией, а он сам себе соответствует. Подсчитаем число различных полиномов Жегалкина. Отметим, что одночленов, составленных из произведений переменных из множества , имеется . Действительно, каждому такому одночлену взаимно однозначно соответствует последовательность из 0 и 1 длины . Если переменная входит в произведение, то на i-м месте в соответствующей последовательности стоит 1, в противном случае – 0. А таких последовательностей, как легко понять, ровно . Пронумеруем их. Теперь установим взаимно однозначное соответствие между полиномами Жегалкина и последовательностями из 0 и 1 длины . Если одночлен входит в полином, то соответствующая координата в последовательности, ему соответствующей, будет равна 1, в противном случае она равна 0. Так как таких последовательностей , то и различных полиномов Жегалкина будет . Получаем, что отображение установлено между равномощными конечными множествами и является отображением на все , а это возможно только при взаимно однозначном отображении. Это и требовалось доказать.

Функционально полные системы функций

По множеству булевых функций построим совокупность множеств.

, , .

Таким образом мы определили совокупность всевозможных суперпозиций функций из .

Определение 3. Система функций называется функционально полной, если множество совпадает с совокупностью всех булевых функций.

Другими словами, система булевых функций является функционально полной, если любая булева функция получается как суперпозиция функций их этого множества.

ТЕОРЕМА 5. Система функций является функционально полной.

Этот факт следует из того, что для каждой булевой функции существует ДНФ (КНФ), ей эквивалентная. А любая нормальная форма содержит только три логические операции, входящие в множество .

Введем понятие сводимости на совокупностях булевых функций.

Одно совокупность булевых функций сводится к другой, если класс булевых функций порожденных суперпозициями функций из второго класса, содержится в классе булевых функций, порожденных суперпозициями функций из первой совокупности.

ТЕОРЕМА 6. Отношение на подмножествах булевых функций является частичным порядком, т.е. удовлетворяет свойствам рефлексивности, транзитивности и антисимметричности.

Доказательство. Рефлексивность очевидна .

Установим транзитивность.

Проверим антисимметричность.

Другими словами, если совокупности булевых функций сводятся друг к другу, то они порождают одно и тоже множество булевых функций.

ТЕОРЕМА 7. Если система булевых функций полна и имеет место сводимость , то и система будет полной системой булевых функций.

Доказательство. Из условия теоремы имеем включения . А это гарантирует равенство , что и требовалось.

Для того, чтобы установить сводимость одной совокупности булевых функций к другой, как легко понять, достаточно выразить функции из первой совокупности через функции из второй совокупности. Просто все операции в формуле из первой совокупности необходимо заменить их выражениями через функции из второй совокупности, что дает выражение булевой функции через функции из второй совокупности.

Понятие сводимости совокупностей булевых функций в отдельных случаях упрощает понимание полноты выбранной совокупности.

ТЕОРЕМА 8. а) Система функций функционально полна.

б) Система функций функционально полна.

Действительно, по закону де-Моргана имеем , что дает сводимость . А тогда из полноты системы следует полнота системы . Аналогично доказывается и вторая часть теоремы.

Определение 4. Булева функция называется функционально полной, если функционально полна система, состоящая из одной этой функции.

ТЕОРЕМА 9. а) Штрих Шеффера является функционально полной булевой функцией.

б) Стрелка Пирса является функционально полной булевой функцией.

Доказательство. Рассмотрим систему, состоящую только из штриха Шеффера. . Покажем, что . Действительно, имеем , . Так как система функционально полна, то и система является функционально полной.

Введем систему , состоящую только из стрелки Пирса. Так как выполняются эквивалентности , , то имеем сводимость . А в силу полноты системы имеем функциональную полноту и системы . Что и требовалось доказать.