4. Приложения криволинейного интеграла второго рода.

1. Вычисление площади.

Рассмотрим область , ограниченную контуром . Площадь области можно вычислить с помощью криволинейного интеграла второго рода по формуле

.

2. Вычисление работы, совершаемой переменной силой.

Рассмотрим силу , действующую на материальную частицу, перемещающуюся по кривой от точки до точки . Работу этой силы можно вычислить по формуле

.

5. Независимость криволинейного интеграла второго рода от пути интегрирования.

Если подынтегральное выражение является полным дифференциалом, то результат вычисления криволинейного интеграла второго рода не зависит от пути интегрирования, а зависит только от начальной и конечной точки интегрирования. Для этого необходимо и достаточно выполнение равенства

.

В этом случае криволинейный интеграл может быть вычислен с помощью формулы Ньютона-Лейбница

,

где и - координаты соответственно начальной и конечной точек кривой , а - некоторая первообразная для полного дифференциала . Эта первообразная может быть вычислена с помощью двух равносильных формул

Начальную точку выбирают с учетом того, чтобы подынтегральные функции были наиболее простыми.

6. Криволинейный интеграл второго рода по пространственной кривой.

1. Вычисление интеграла.

Если пространственная кривая задается параметрически , то при вычислении криволинейного интеграла второго рода по пространственной кривой используется формула

.

2. Вычисление работы.

Работа переменной силы , действующей на материальную частицу, перемещающуюся по пространственной кривой от точки до точки , вычисляется по формуле

.

3. Условие независимости криволинейного интеграла от пути интегрирования

Если подынтегральное выражение является полным дифференциалом, то результат вычисления криволинейного интеграла второго рода не зависит от пути интегрирования, а зависит только от начальной и конечной точки интегрирования. Для этого необходимо и достаточно выполнение равенств

.

В этом случае криволинейный интеграл может быть вычислен с помощью формулы Ньютона-Лейбница

,

где и - координаты соответственно начальной и конечной точек кривой , а - некоторая первообразная для полного дифференциала .

Для вычисления первообразной можно, например, использовать формулу

.

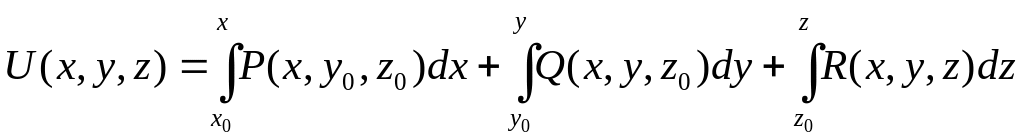4. Преобразование криволинейного интеграла второго рода к криволинейному интегралу первого рода.

Используя выражения для направляющих косинусов

,

криволинейный интеграл второго рода можно преобразовать к криволинейному интегралу первого рода

.

Направляющие косинусы определяются как косинусы углов между вектором, касательным к кривой, и осями координат. Если кривая задана в параметрическом виде , то эти косинусы равны

, ,

ЗАДАЧИ

1. Задачи минимального уровня сложности.

1. Вычислить криволинейные интегралы.

9.1. , где - дуга параболы от точки до точки .

9.2. , где - дуга первой арки циклоиды , пробегаемая в направлении возрастания параметра .

9.3. , где - верхняя половина эллипса , пробегаемая по ходу часовой стрелки.

9.4. , взятый вдоль окружности против хода часовой стрелки.

9.5. , взятый вдоль отрезка биссектрисы второго координатного угла, если абсцисса точки равна 2 и ордината точки равна 2.

2. Вычислить криволинейные интегралы от выражений, являющихся полными дифференциалами.

9.6. .

9.7. .

9.8. .

9.9. (по пути, не пересекающему ось ).

9.10. (по пути, не пересекающему прямую ).

9.11.

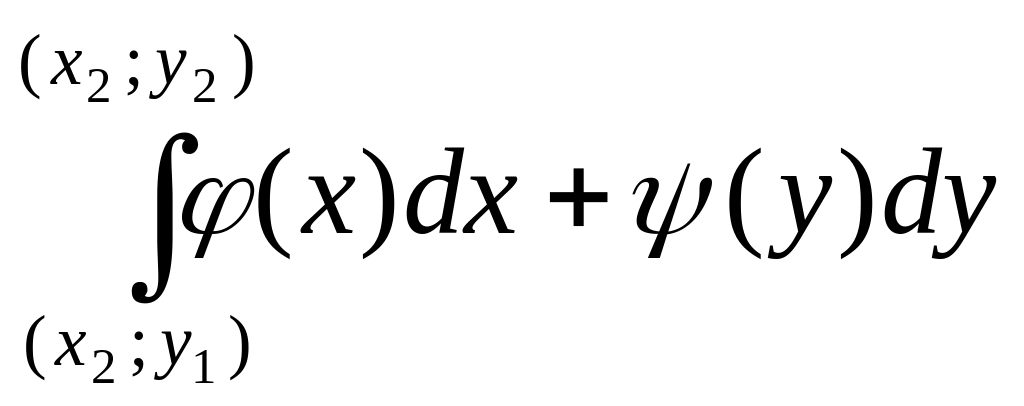
3. Найти первообразные функций подынтегральных выражений и вычислить интегралы.

9.12. .

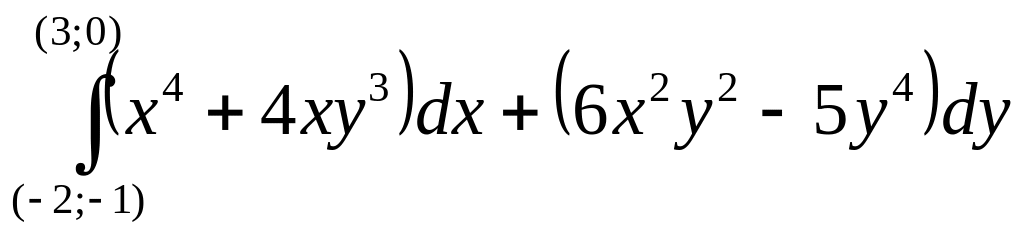9.13. (путь интегрирования не пересекает прямой ).

9.14. (путь интегрирования не пересекает прямой ).

9.15. .

4. Вычислить криволинейные интегралы, взятые вдоль пространственных кривых.

9.16. , где - виток винтовой линии .

9.17. , где - окружность , пробегаемая в направлении возрастания параметра.

9.18. , где - дуга окружности , расположенная по ту сторону от плоскости , где .

5. Вычислить криволинейные интегралы от полных дифференциалов,

взятые вдоль пространственных кривых.

9.19. .

9.20. .

9.21. .

9.22. (путь интегрирования расположен в первом октанте).

6. Формула Грина.

9.23. Применяя формулу Грина, вычислить , где - пробегаемый в положительном направлении контур треугольника с вершинами в точках . Проверить найденный результат, вычисляя интеграл непосредственно.

9.24. Применяя формулу Грина, вычислить интеграл ,где - окружность , пробегаемая против хода часовой стрелки.

9.25. Вычислить двумя способами интеграл ,где - окружность : 1) непосредственно, 2) с помощью формулы Грина.

9.26. Вычислить , где : 1) эллипс ; 2) окружность . Интегрирование ведется в положительном направлении. (Вычисление провести двумя способами:1) непосредственно, 2) с помощью формулы Грина.)

7. Вычислить площадь фигур, ограниченных замкнутыми линиями.

9.27. Окружностью .

9.28. Эллипсом .

9.29. Кардиоидой .

9.30. Астроидой .

9.31. Петлей линии .

9.32. Петлей линии .

9.33. Лемнискатой Бернулли .

8. Вычислить работу силы.

9.34. В каждой точке плоскости на материальную точку действует постоянная сила , направленная по оси абсцисс. Найти работу, совершаемую этой силой, при движении точки по дуге окружности , лежащей в первом квадранте.

9.35. В каждой точки плоскости на материальную точку действует сила , проекции которой на оси координат равны . Вычислить работу силы при перемещении точки из начала координат в точку : 1) по прямой ; 2) по параболе ; 3) по двухзвенной ломанной, стороны которой параллельны осям координат (два случая).

9.36. В каждой точке эллипса приложена сила , пропорциональная по величине расстоянию от точки до центра эллипса и направленная к центру эллипса. А) Вычислить работу силы при перемещении точки вдоль дуги эллипса, лежащей в первом квадранте. B) Найти работу, если точка обходит весь эллипс.

9.37. Проекции силы на оси координат задаются формулами . Показать, что работа силы при перемещении точки зависит только от начального и конечного ее положения и не зависит от формы пути. Вычислить величину работы при перемещении из точки в точку .

9.38. Сила по величине обратно пропорциональна расстоянию точки ее приложения от плоскости и направлена к началу координат. Вычислить работу силы при движении материальной точки по прямой от точки до точки .

9.39. Сила по величине обратно пропорциональна расстоянию точки ее приложения от оси , перпендикулярна этой оси и направлена к ней. Найти работу силы при движении точки под действием этой силы по окружности от точки до точки .

9.40. Доказать, что работа силы тяготения двух точечных масс, совершаемая при перемещении одной из них, не зависит от формы пути. Величина силы тяготения задается законом Ньютона , где - расстояние между точками, и - массы, сосредоточенные в этих точках, - гравитационная постоянная.