
- •Глава 1 Внешние модели данных
- •1.1. Общие положения
- •1.2. Иерархическая модель
- •1.3. Целостность иерархической модели
- •Уникальность
- •Обязательность и множественность
- •Кортежи
- •Виртуальные атрибуты
- •Правила активности
- •1.4. Построение иерархических моделей
- •Ориентация модели
- •Выбор ключевых атрибутов
- •3 Посвященному пользователю этот набор цифр — номер зачетной книжки — тоже может сказать кое-что; например, первые две цифры — о годе поступления студента.
- •1.5. Модель «гиперкуб данных»
1.5. Модель «гиперкуб данных»
Иерархическая модель является распространенной, но не единственной моделью для внешнего локального представления данных. В OLAP-системах (см. примечание на с. 7) для этого применяются многомерные модели типа «гиперкуб данных». Обсудим их в общих чертах.
Г иперкуб
данных (Data
Hypercube)
или просто куб данных (Data
Cube)
— это организация данных в виде
многомерного массива (рис. 2.20). Куб
данных имеет несколько независимых
измерений (Dimensions),
задающих систему координат пространства
данных (на рисунке показан трехмерный
куб с измерениями (X,
У и
Z).
Каждое
измерение — это конечное множество
однородных значений данных, образующее
грань куба, оно соответствует домену
в модели, рассмотренной ранее (на рисунке
в качестве значений измерений
приведены отрезки натурального
числового ряда, в общем случае это могут
быть годы, месяцы, регионы, города,
названия предприятий, виды продукции
и т. п.). Некоторое значение измерения
задает координату по этому измерению.
Совокупность координат по всем измерениям
идентифицирует ячейку (Cell)или
элемент (Item)
куба (на рисунке показана ячейка Cijk
с
координатами (Xi,Yj,Zk),
т.е.
соответствующая значению iизмерения
X,
значению
jизмерения
Y
и
значению к
измерения
Z).
В
каждой ячейке размещены в общем случае
несколько показателей или фактов (Facts)
— данных, хранящихся в кубе (на рисунке
с каждой ячейкой ассоциировано р
фактов:
(f1,f2…..fp).
Обычно все факты одного q-ro
типа
в кубе однородны, т.е. являются различными
значениями некоторого показателя
процесса, информация о котором собрана
в хранилище данных. Как правило,
это числовые значения (так называемые
статистики)1:
количества и стоимости поставленных
или проданных товаров, произведенной
продукции, суммы банковских операций
и другие данные, привязанные к координатам
времени, места, условий и т.д. Для гиперкуба
предусмотрен ряд специфических операций
манипулирования данными, в том числе:
иперкуб
данных (Data
Hypercube)
или просто куб данных (Data
Cube)
— это организация данных в виде
многомерного массива (рис. 2.20). Куб
данных имеет несколько независимых
измерений (Dimensions),
задающих систему координат пространства
данных (на рисунке показан трехмерный
куб с измерениями (X,
У и
Z).
Каждое
измерение — это конечное множество
однородных значений данных, образующее
грань куба, оно соответствует домену
в модели, рассмотренной ранее (на рисунке
в качестве значений измерений
приведены отрезки натурального
числового ряда, в общем случае это могут
быть годы, месяцы, регионы, города,
названия предприятий, виды продукции
и т. п.). Некоторое значение измерения
задает координату по этому измерению.
Совокупность координат по всем измерениям
идентифицирует ячейку (Cell)или
элемент (Item)
куба (на рисунке показана ячейка Cijk
с
координатами (Xi,Yj,Zk),
т.е.
соответствующая значению iизмерения
X,
значению
jизмерения
Y
и
значению к
измерения
Z).
В
каждой ячейке размещены в общем случае
несколько показателей или фактов (Facts)
— данных, хранящихся в кубе (на рисунке
с каждой ячейкой ассоциировано р
фактов:
(f1,f2…..fp).
Обычно все факты одного q-ro
типа
в кубе однородны, т.е. являются различными
значениями некоторого показателя
процесса, информация о котором собрана
в хранилище данных. Как правило,
это числовые значения (так называемые
статистики)1:
количества и стоимости поставленных
или проданных товаров, произведенной
продукции, суммы банковских операций
и другие данные, привязанные к координатам
времени, места, условий и т.д. Для гиперкуба
предусмотрен ряд специфических операций
манипулирования данными, в том числе:
срез (Slice) путем фиксации координат куба по некоторым измерениям (на рисунке с помощью серой заливки показан срез по Xi);
поворот (Rotation), заключающийся в изменении порядка следования измерений в кубе удобным для пользователя образом;
агрегирование (Aggregation), позволяющее построить из куба или его среза новый куб путем укрупнения (группирования) определенных ячеек;
детализация (Drill-down), состоящая в разукрупнении агрегированных ячеек.

Разреженность (Sparse) куба данных, характерная для многих практических приложений многомерных моделей данных, в данном примере проявляется в том, что значительная часть ячеек будет незаполненной (иметь неопределенные значения Null). Большинство предметов изучается в одном семестре, немногие — в двух, и лишь совсем немногие — в трех или четырех. Поэтому оценки по тем или иным предметам могут присутствовать лишь в срезах соответствующих семестров. Не будет оценок у студентов, которые еще не приступили к изучению данных предметов. Студенты разных специальностей изучают разные наборы предметов в соответствии со своими учебными планами и т. д. Подобное нерациональное использование пространства гиперкуба не рассматривается в OLAP как «криминал», главный фактор — удобство представления данных пользователю2.
Агрегирование ячеек гиперкуба — принципиально важная операция манипулирования данными, учитывая, что основное назначение этой модели — многомерный статистический анализ данных в интересах поддержки принятия решений. Так, в рассмотренном выше примере может потребоваться анализировать успеваемость не на уровне отдельных студентов, а на уровне студенческих групп, специальностей или целых направлений подготовки специалистов. Или не для отдельных предметов, а для циклов предметов (гуманитарных, естественнонаучных, специальных и т. д.). Для этого нужно группировать вместе ячейки, относящиеся к одной студенческой группе, специальности, направлению, циклу предметов и т. д. и для таких укрупненных ячеек вычислять укрупненные (агрегированные) показатели. В свою очередь, для этого в модели гиперкуба необходимы сведения двух родов:
критерии группирования, т.е. предикаты, позволяющие относить ячейки к той или иной группе, а группы — к той или иной супергруппе и т. д.;
правила вычисления агрегированных данных, позволяющие на основе исходных показателей укрупняемых ячеек, получать показатели укрупненных ячеек3.
Иерархии значений, устанавливаемые для измерений гиперкуба, — способ задания критериев группирования в процессе агрегирования данных. Для каждого измерения гиперкуба может быть задано иерархическое (древовидное) упорядочивание значений координат. В общем случае таких упорядочиваний может быть несколько для одного измерения. Подобная иерархия объединяет значения координат данного измерения в группы, те — в супергруппы и т.д., т.е. задает группирование срезов куба по соответствующему измерению. Одновременное группирование срезов по разным измерениям позволяет решить задачу агрегирования нужных ячеек.

Приведенная иерархия позволяет для каждого студента определить, к какой студенческой группе он приписан, на какой специальности и по какому направлению он обучается. Это, в свою очередь, позволяет группировать срезы куба по измерению «Студенты», объединяя в одну группу срезы отдельных студентов, обучающихся в одной студенческой группе, на одной специальности или по одному направлению. Каждая группа срезов в результате агрегирования заменяется одним укрупненным срезом, в котором объединяются ячейки, соответствующие разным студентам и одинаковым значениям координат по остальным измерениям (рис. 1.22, б).
Какие же данные доступны для анализа при использовании агрегированного куба? Для анализа успеваемости обычно оперируют такими статистиками, как средний балл и процентные соотношения тех или иных оценок студентов. Пусть требуется анализировать средний балл. Тогда в качестве показателей, хранимых в ячейках куба, достаточно использовать две статистики: суммарную оценку и количество студентов; разделив первое на второе, получим средний балл. При вычислении агрегированных показателей одноименные показатели исходных ячеек суммируются.
Диаграмма модели «гиперкуб» должна, в соответствии с изложенным выше, содержать сведения о типах фактов, хранимых в ячейках куба, и о правилах вычисления агрегированных показателей для каждого факта, об измерениях куба, об иерархиях значений по каждому измерению. Как и в случае «сложной таблицы» для этого используется иерархическая структура (рис. 1.23). Верхний уровень иерархии представляет сам гиперкуб, имя которого записано внутри символа трехмерного параллелепипеда. На втором уровне представлены измерения куба и хранимые в нем факты. Измерения изображены в виде прямоугольников, в которых записаны их имена. Иерархия значений в измерениях задается с помощью вложенных агрегатов-элементов измерений (обратите внимание на то, что иерархия задана в обратном порядке, от «ребенка» к «родителю», ср. рис. 1.22, а). Каждое измерение представлено в форме «сложной таблицы», содержащей значения измерения и показатели иерархии. Факты представлены агрегатом, атрибуты которого соответствуют показателям куба.
Концептуальные отличия «гиперкуба» от «сложной таблицы» требуют дополнительного обсуждения, поскольку диаграммы этих двух моделей очень похожи и возникает подозрение, не являются ли они, по-существу, одним и тем же в плане возможностей доступа к данным? Такое подозрение является обоснованным, поскольку, как будет показано ниже, гиперкуб всегда можно без потери информации представить в виде сложной таблицы. Однако имеются отличия, связанные с восприятием данных пользователями в этих моделях:

• разнородность свойств и однородность фактов. Если содержимое сложной таблицы воспринимается как совокупность кортежей (строк) разнородных сведений об объектах предметной области, то содержимое гиперкуба — как совокупности однородных показателей, привязанных к координатам многомерного пространства данных. Разнородность гиперкуба — это разнородность (между собой) его измерений, а также разнородность иерархической организации однородных значений измерений.
Представление гиперкуба сложной таблицей. Из сказанного выше следует, что иерархическая модель является более универсальной моделью данных, чем гиперкуб — специализированная модель для отражения однородных фактов в пространстве разнородных измерений. Следовательно, гиперкуб может быть представлен эквивалентной сложной таблицей. Обсудим, как это сделать.
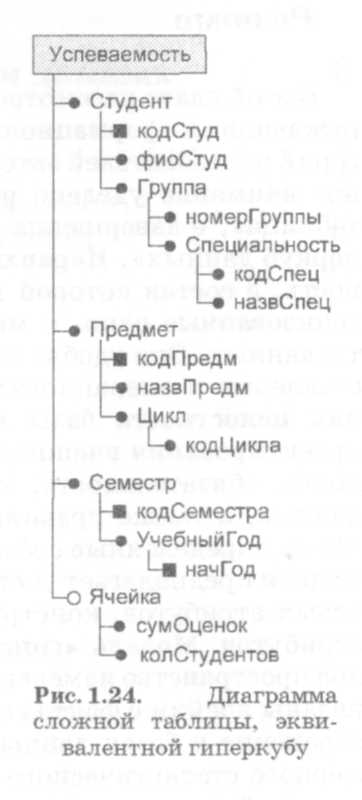
Пустые ячейки, являющиеся вполне естественными в гиперкубе, могут «потеряться» при переходе к сложной таблице. Если таблица заполняется путем занесения строк-ячеек, содержащих факты, то в ней хранятся значения только «актуальных координат»4 ячеек куба, в которых присутствуют факты. Сведения о координатах с пустыми ячейками теряются. Если полные сведения о составе координат куба являются существенными, то необходимо разместить в таблице строки, соответствующие всем ячейкам куба, используя Null-значения фактов в незаполненных ячейках (что, вообще говоря, не приветствуется, см. гл. 6).
1 Статистикой (наукой) занимаются статистики (ученые), которые изучают статистики (показатели).
2 Напомним, что рассматривается концептуальный уровень проектирования, на котором вопросы производительности базы данных не являются главными. При реализации гиперкуба в рамках построенной концептуальной модели применяются различные способы сокращения неиспользуемой памяти.
3 Отметим отличие понятий агрегата / агрегирования в рассмотренной выше иерархической модели и в модели гиперкуба. В первом случае имеется в виду именованное объединение (укрупнение) нескольких атрибутов, позволяющее манипулировать целиком кортежами значений атрибутов (экземплярами атрибутов) наряду с доступом к отдельным атрибутам. Во втором случае укрупнение ячеек в процессе агрегирования сопровождается заменой их исходного содержимого на некоторое новое значение, например, сумму исходных значений.
4 По аналогии с понятием актуального домена, т.е. множества тех значений домейа, которые используются в настоящее время в качестве значений атрибутов в базе данных.
Резюме
В этой главе рассмотрены внешние модели данных, отражающие информационные потребности отдельных категорий пользователей автоматизированной системы. Основное внимание уделено иерархической модели «сложная таблица», в завершение кратко рассмотрена модель «гиперкуб данных». Иерархическая модель определяет сущность, в состав которой могут входить иерархически организованные одно- и многозначные атрибуты и агрегаты данных. Она удобна в качестве модели внешнего представления в операциональных базах данных. Ограничения целостности базы данных задаются уже на этапе проектирования внешних моделей и учитывают уникальность, обязательность, множественность, виртуальность данных, а также правила активности базы данных в ответ на определенные события. Построение иерархической модели предполагает учет ориентации модели, выбор ключевых атрибутов, конструирование агрегатов, обобщение атрибутов. Модель «гиперкуб данных» задает многомерное пространство измерений, к координатам которого привязаны ячейки с фактами. Она получила широкое распространение в базах данных, предназначенных для многомерного статистического анализа и поддержки принятия решений.
