Уравнения математической физики 3
Задача
1. Найдите в
указанной области отличные от
тождественного нуля решения
дифференциального уравнения,
удовлетворяющие заданным краевым
условиям (задача Штурма-Лиувилля).
1.1.
1.2.
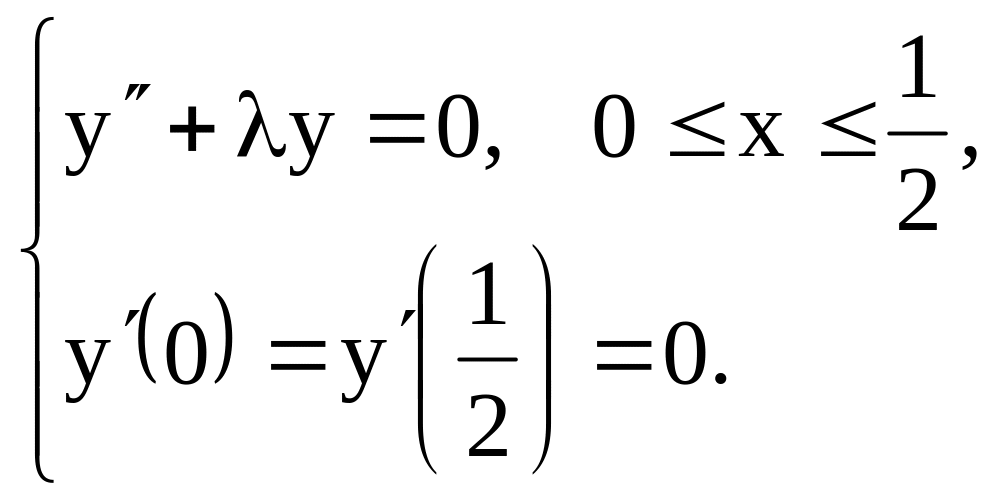
1.3.
1.4.
1.5.
1.6.
1.7.
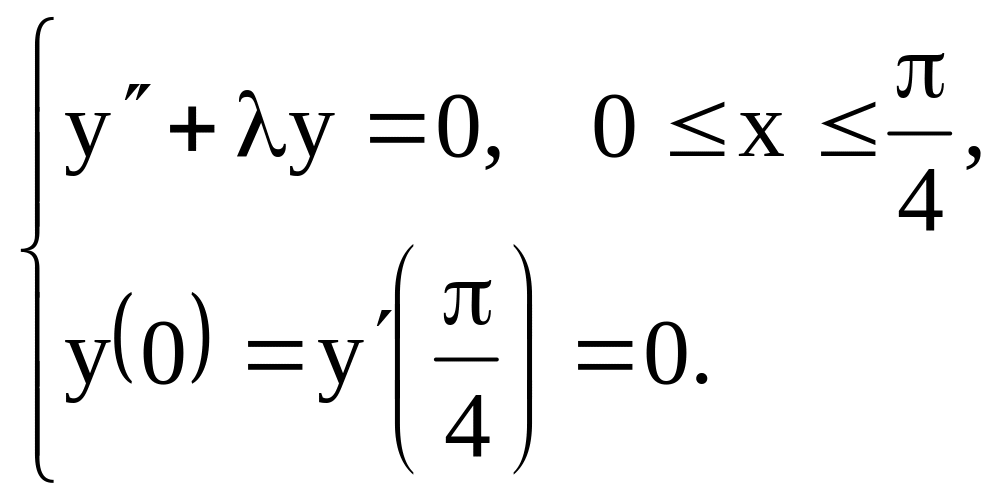
1.8.
1.9.
1.10.
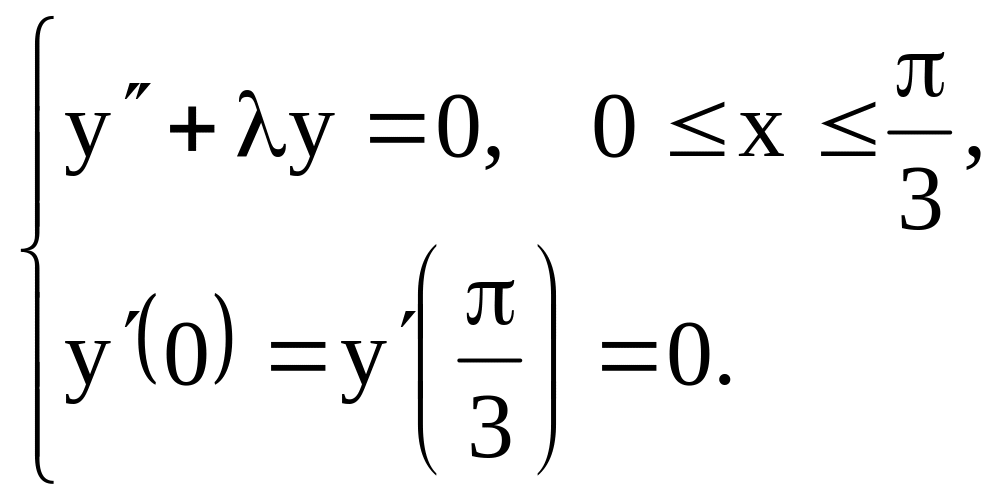
1.11.
1.12.
1.13.
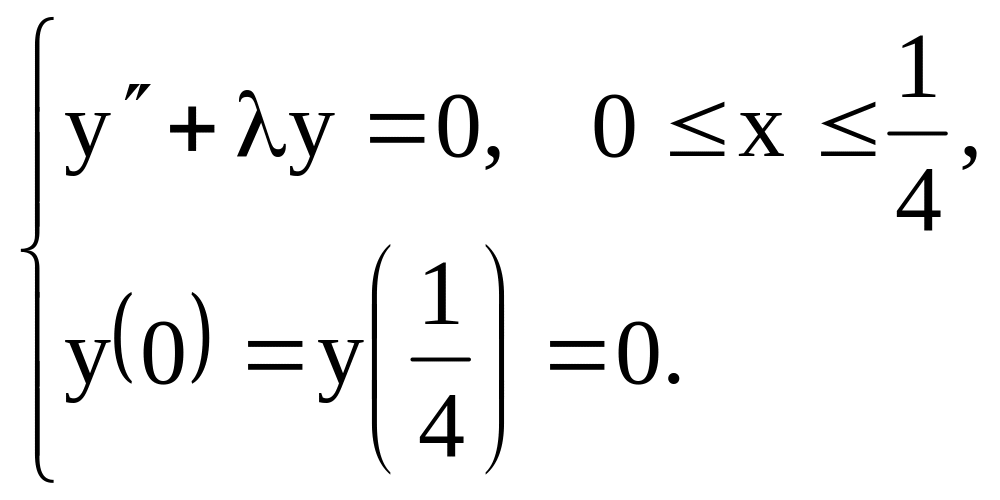
1.14.
1.15.
1.16.
1.17.
1.18.
1.19.
1.20.
1.21.
1.22.
1.23.
1.24.
1.25.
1.26.
1.27.
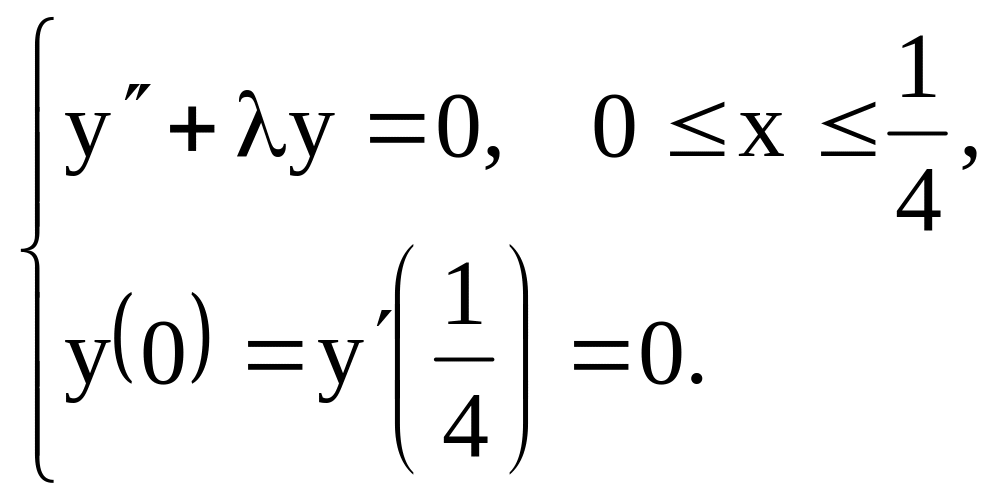
1.28.
1.29.
1.30.
Задача 2. Найдите общее решение уравнения, приведя его к каноническому виду.
2.1.
.
2.2.
.
2.3.
.
2.4.
.
2.5.
.
2.6.
.
2.7.
.
2.8.
.
2.9.
.
2.10.
.
2.11.
.
2.12.
.
2.13.
.
2.14.
.
2.15.
.
2.16.
.
2.17.
.
2.18.
.
2.19.
.
2.20.
.
2.21.
.
2.22.
.
2.23.
.
2.24.
.
2.25.
.
2.26.
.
2.27.
.
2.28.
.
2.29.
.
2.30.
.
Задача 3. Найдите общее решение уравнения, приведя его к каноническому виду.
3.1.
.
3.2.
.
3.3.
.
3.4.
.
3.5.
.
3.6.
.
3.7.
.
3.8.
.
3.9.
.
3.10.
.
3.11.
.
3.12.
.
3.13.
.
3.14.
.
3.15.
.
3.16.
.
3.17.
.
3.18.
.
3.19.
.
3.20.
.
3.21.
.
3.22.
.
3.23.
.
3.24.
.
3.25.
.
3.26.
.
3.27.
.
3.28.
.
3.29.
.
3.30.
.
Задача 4. Найдите общее решение уравнения
с помощью метода Лапласа, приведя его к каноническому виду (исходные данные в таблице).
Метод Лапласа
Уравнение
,
где
–
числа, можно привести к виду
.
Тогда если
,
то исходное уравнение можно привести
к виду
с помощью замены
.
В-т |
|
|
|
|
|
|
|
1 |
4 |
3 |
–1 |
11 |
6 |
7 |
|
2 |
75 |
20 |
1 |
10 |
4 |
–5 |
|
3 |
27 |
12 |
1 |
9 |
1 |
–6 |
|
4 |
1 |
36 |
243 |
–1 |
9 |
–2 |
|
5 |
1 |
24 |
108 |
1 |
–6 |
–2 |
|
6 |
1 |
12 |
27 |
–6 |
–12 |
–7 |
|
В-т |
|
|
|
|
|
|
|
7 |
1 |
3 |
2 |
3 |
2 |
–4 |
|
8 |
192 |
32 |
1 |
–16 |
2 |
–8 |
|
9 |
3 |
32 |
64 |
8 |
16 |
–3 |
|
10 |
16 |
16 |
3 |
12 |
1 |
–4 |
|
11 |
1 |
32 |
192 |
–1 |
8 |
–2 |
|
12 |
1 |
16 |
48 |
5 |
12 |
–6 |
|
13 |
25 |
20 |
3 |
10 |
8 |
–3 |
|
14 |
108 |
24 |
1 |
12 |
4 |
–5 |
|
15 |
1 |
8 |
12 |
4 |
4 |
–5 |
|
16 |
3 |
4 |
1 |
–1 |
1 |
–2 |
|
17 |
1 |
28 |
147 |
3 |
7 |
–4 |
|
18 |
48 |
16 |
1 |
–12 |
1 |
–6 |
|
19 |
4 |
8 |
3 |
4 |
4 |
1 |
|
20 |
49 |
28 |
3 |
–7 |
3 |
–6 |
|
21 |
1 |
20 |
75 |
4 |
10 |
–5 |
|
22 |
3 |
20 |
25 |
8 |
10 |
–3 |
|
23 |
12 |
8 |
1 |
4 |
4 |
–5 |
|
24 |
3 |
8 |
4 |
8 |
4 |
–3 |
|
25 |
2 |
3 |
1 |
6 |
2 |
–8 |
|
26 |
147 |
28 |
1 |
7 |
3 |
–4 |
|
27 |
1 |
4 |
3 |
–1 |
1 |
–2 |
|
28 |
64 |
32 |
3 |
–8 |
3 |
–6 |
|
29 |
3 |
16 |
16 |
5 |
4 |
–2 |
|
30 |
3 |
28 |
49 |
5 |
7 |
–2 |
|
