6.6. Переходные колебания в линейных электрических цепях с одним реактивным элементом при типовых воздействиях.

Включение в RC-цепь постоянной ЭДС.

Рассмотрим процесс RC-цепи при подключении заряженного конденсатора с напряжением к источнику постоянной ЭДС Е.

рис(2.0.8)

Применим для данной цепи после коммутации второй закон Кирхгофа.

Составим дифференциальное уравнение относительно напряжения на емкости

, учитывая, что

или

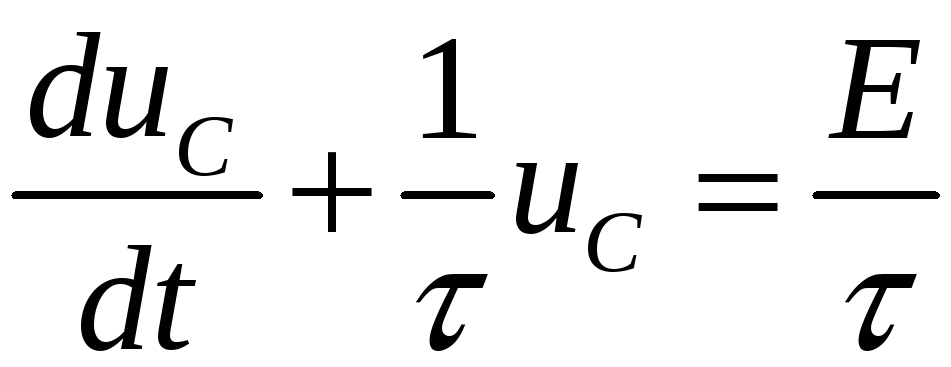
где

Получаем линейное диф.уравнение первого порядка с неизвестной функцией . По своей структуре оно аналогично )2.5.3) , в котором

Найдем свободную составляющую, для чего положим

Этому однородному дифференциальному уравнению соответствует характеристический полином.

так как

Корень этого полинома равен , тогда решение этого однородного дифференциального уравнения можно записать в виде

Где А – постоянная интегрирования.

Тогда общее решение неоднородного дифференциального уравнения запишем в виде суммы свободной и установившейся составляющей напряжения:

рис(2.0.9)

В установившемся режиме конденсатор зарядится до напряжения Е, очевидно, что

Следовательно:

Постоянную А найдем из закона коммутации

При получаем

То есть или

Окончательно получим

= +

полный отклик переходное состояние установившееся состояние

Найдем ток

рис(2.1.0)

Найдем напряжение на резисторе R

Заметим, что если , то переходный процесс отсутствует.

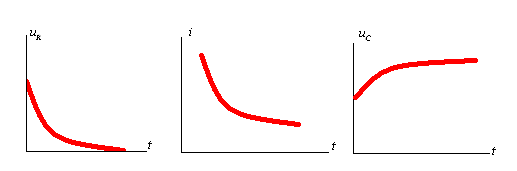
График функций при переходных процессах

Включение в RL-цепь постоянной ЭДС.

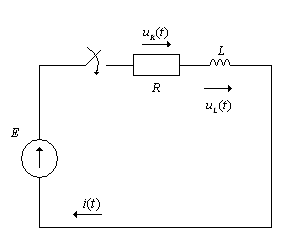рис(2.1.1)

Для данной цепь после коммутации запишем второй закон Корхгофа

Составим диф.уравнение, т.к. и , то

Получим интегральное уравнение.

Перейдем к дифференциальному уравнению, продифференцировав обе части уравнения по t. Учитывая, что производная от интеграла равна подинтегральному выражению

или где

Составим характеристический многочлен и найдем корень

Тогда ,

Так как диф.уравнение однородно, общее решение будет

Найдем постоянную интегрирования А согласно схеме

рис(2.1.2)

Так как и , то

Окончательно получим

рис(2.1.3)

На рис. (2.1.3) показана функция при переходном процессе.

Ускоренный метод.

Из дифференциального исчисления известно, что общим решением дифференциального уравнения 1-го порядка с постоянными коэф. И пост. Правой части

и , является функция

где то есть

http://MATI.fatal.ru