Тема № 4. Двойственные задачи.

Взаимно двойственные задачи линейного программиро­вания и их свойства. Алгоритм составления двойственной задачи. Экономическая интерпретация двойствен­ной задачи.

Содержание основных понятий темы

Задача 1.

Имеются два вида сырья и , на предприятии к концу года. Остатки сырья составляют 35 и 20 единиц соответственно. Из этого сырья, с одной стороны, можно наладить производство трех видов товаров, и от реализации единицы каждого вида товара получить прибыль 7, 6 и 18 ден. ед. соответственно. Нормы расхода приведены в таблице.

Виды товаров			Прибыль
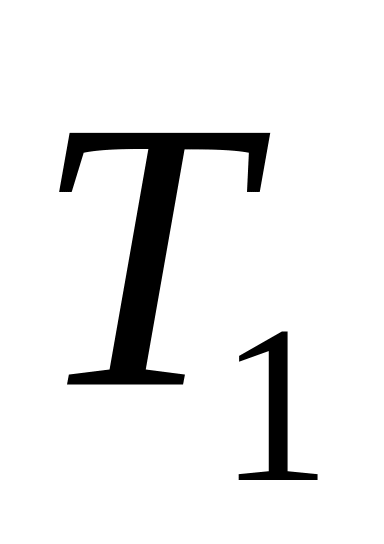
	1	2	7
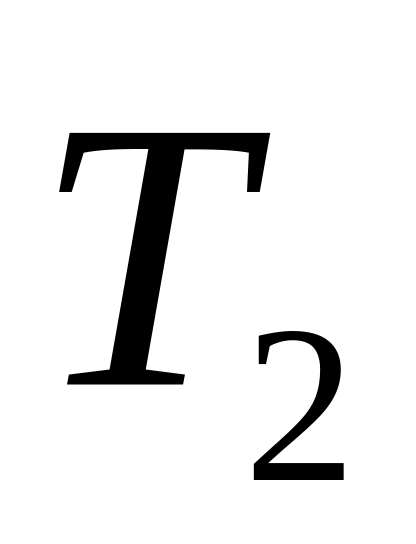
	1	1	6
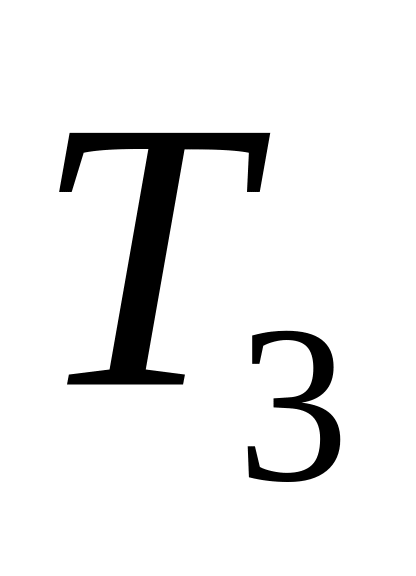
	5	2	18
Запасы	35	20

С другой стороны, это сырье можно продать на сторону какой-либо нуждающейся в этом сырье организации. Как следует поступить руководству предприятия?

Решение.

При исследовании налаживания выпуска товаров возникает вопрос о плане выпуска. Этот план задается количеством единиц товара, которое будет произведено из оставшегося сырья. Обозначим эти количества соответственно. Задачу максимизации прибыли от выпуска товаров можно сформулировать, следующем образом:

при условиях

При продаже сырья другой организации возникает вопрос о цене сырья. Обозначим цену единицы сырья через , а сырья - через . Выручка от продажи сырья должна быть не меньше, чем прибыль от реализации готового изделия. В противном случае лучше изготовить товар и получить от него прибыль. Это требование приведет к неравенствам

Для покупателя единственное пожелание состоит в сокращении расходов, т.е. в минимизации функции

Таким образом, задачу минимизации расходов от покупки сырья можно сформулировать следующим образом:

при условиях

.

Сравнивая эти две задачи, видим, что они являются двойственными друг другу. Поэтому, используя критерий оптимальности, находим, что максимальная прибыль, которую можно получить за счет изготовления из остатков сырья продукции, совпадает с выручкой от продажи сырья, т.е.

Если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая, причем оптимальные значения их линейных функций равны.

Экономически это можно интерпретировать так: предприятию безразлично, производить ли про­дукцию по оптимальному плану и получить максимальную прибыль (выручку) либо продавать ресурсы по оптималь­ным ценам и возместить от продажи равные ей минимальные затраты на ресурсы .

Обе задачи обладают следующими свойствами:

1. В одной задаче ищут максимум линейной функции, в другой –минимум.

2. Коэффициенты при переменных в линейной функции одной за­дачи являются свободными членами системы ограничений в другой.

3. Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида ≤, а в задаче минимизации - все неравенства вида ≥.

4. Матрицы коэффициентов при переменных в системах ограни­чений обеих задач являются транспонированными друг к другу.

5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче.

6. Условия неотрицательности переменных имеются в обеих задачах.

Алгоритм составления двойственной задачи:

1. Привести все неравенства системы ограничений исходной за­дачи к одному смыслу: если в исходной задаче ищут максимум линей­ной функции, то все неравенства системы ограничений привести к виду ≤ , а если минимум - к виду ≥. Для этого неравенства, в которых дан­ное требование не выполняется умножить на (-1).

2. Составить расширенную матрицу системы A_ij, в которую вклю­чить матрицу коэффициентов при переменных A, столбец свободных членов системы ограничений и строку коэффициентов при перемен­ных в линейной функции.

3. Найти матрицу А^Т, транспонированную к матрице A_ij.

4. Сформулировать двойственную задачу на основании полученной матрицы А^Т и условия неотрицательности переменных.

Задача 2.

Составить задачу, двойственную следующей задаче:

при ограничениях:

Решение.

1. Так как исходная задача на максимизацию, то приве­дем все неравенства системы ограничений к виду ≤, для чего обе час­ти первого и четвертого неравенства умножим на -1. Получим

2. Составим расширенную матрицу системы

3. Найдем матрицуA^T транспонированную к А

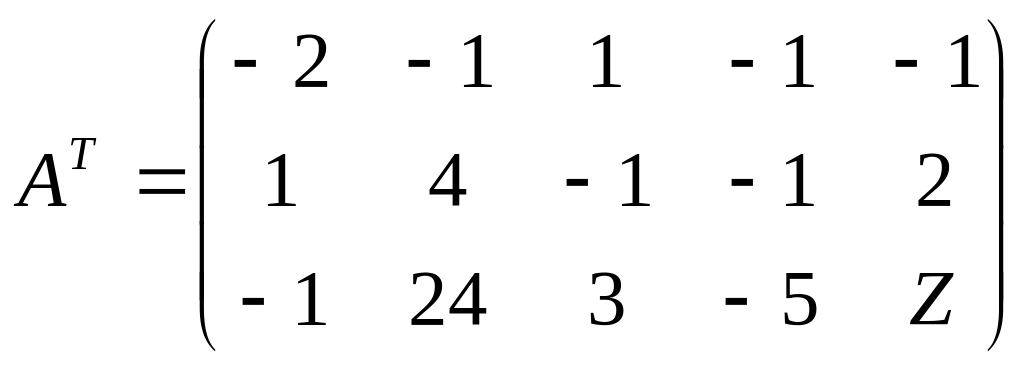
4. Сформулируем двойственную задачу:

при ограничениях

Самостоятельно решите следующие задачи:

3.1. Составить задачу, двойственную следующей задаче:

1) 2)

при ограничениях: при ограничениях:

3) 4)

при ограничениях: при ограничениях:

5) 6)

при ограничениях: при ограничениях:

3.2. Банк имеет на 3 месяца свободные ресурсы в количестве 1 млрд. руб. Вложение в ГКО даст 29%, на межбанковском рынке можно получить 17%, вложение в валюту с последующей конвертацией даст только 14%. Составьте задачу распределения свободных средств с целью максимизации процентного дохода. Составьте двойственную задачу. Какова двойственная оценка ресурса - денег?

3.3. Цех производит трансформаторы двух видов. На один трансформа­тор первого вида нужно 5 кг железа и 3 кг проволоки, второго вида -3 кг же­леза и 2 кг проволоки. От реализация одного трансформатора цех получает прибыль 6 и 5 у.е, соответственно. Цех располагает 4,8 т железа и 3 т прово­локи. Сколько видов продукции производит цех? Сколько видов ресурсов ис­пользуется? Составьте матрицу норм расхода, векторы удельной прибыли и запасов ресурсов. Рассмотрите несколько планов производства и определите, какие из них допустимы. Например, допустимы ли планы , ?

3.4. На лесопилке из еловой и пихтовой древесины делают фанеру и брусы. На 100 м³ фанеры нужно 2 м³ еловой и 6 м³ пихтовой древесины и при­быль равна 170$, На 100 пог. м елового бруса требуется 5 м³, а на 100 пог. м пихтового бруса нужно 4 м³ древесины, прибыль же равна соответственно 80$ и 100$. Сколько видов продукции производит лесопилка? Сколько видов ре­сурсов используется? Составьте матрицу норм расхода, векторы удельной прибыли и запасов ресурсов. Докажите, что фанеру производить невыгодно, и найдите план, дающий максимальную прибыль. Какой ресурс является «узким местом»? каковы двойственные оценки ресурсов?