
- •1. Экспериментальные методы определения максимальной энергии бета-спектра
- •2. Методики на основе метода ослабления для определения максимальной энергии бета-спектра
- •2.1 Методика полного поглощения
- •2.2 Определение граничной энергии бета-спектра по методике 2n– кратного ослабления потока бета-частиц
- •2.3 Методика определения граничной энергии бета-спектра по коэффициенту ослабления потока бета-частиц
- •3. Порядок выполнения работы и обработки результатов измерений
- •3.2 Описание экспериментальной установки
- •3.3 Проведение измерений
2.2 Определение граничной энергии бета-спектра по методике 2n– кратного ослабления потока бета-частиц
Функцию ослабления
можно характеризовать последовательными
значениями толщин
![]() ,
при которых интенсивность потока
бета–частиц уменьшается в 2n–
раз, где n=1,
2, 3 … Значения
зависят от кратности ослабления n,
граничной энергии Еmax
, атомного номера Z
и плотности
поглотителя. Семейство зависимостей
,
при которых интенсивность потока
бета–частиц уменьшается в 2n–
раз, где n=1,
2, 3 … Значения
зависят от кратности ослабления n,
граничной энергии Еmax
, атомного номера Z
и плотности
поглотителя. Семейство зависимостей
![]() ,
полученных полуэмпирическим способом,
позволяет определить значение Еmax
путем
сравнения экспериментальных значений
,
полученных
по измеренной
функции ослабления
,
полученных полуэмпирическим способом,
позволяет определить значение Еmax
путем
сравнения экспериментальных значений
,
полученных
по измеренной
функции ослабления
![]() с рассчитанными полуэмпирическими
зависимостями
с рассчитанными полуэмпирическими
зависимостями
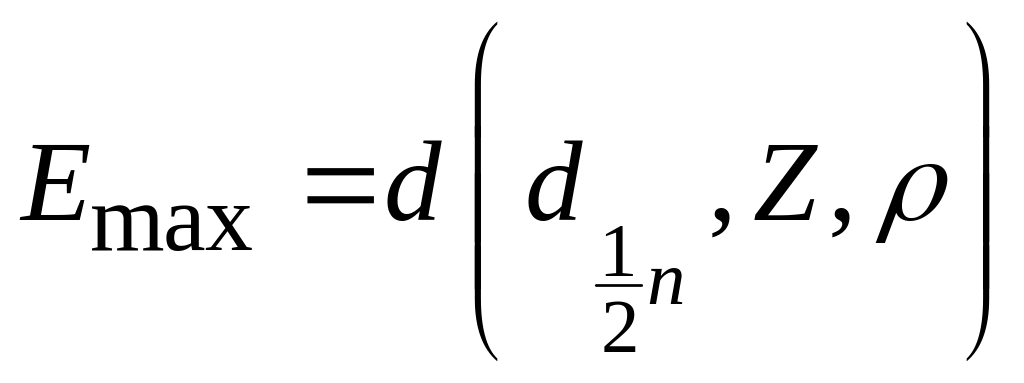 ,
которые обычно представляют в виде
номограммы, графика или таблицы.
,
которые обычно представляют в виде
номограммы, графика или таблицы.
Величина слоя половинного ослабления d1/2 связана с максимальным пробегом , например в алюминии, приближенным соотношением:
d1/2![]() 0,1Rmax
, где
в г/см2.
0,1Rmax
, где
в г/см2.
Для поглотителей с другим атомным номером Z справедливо приближенное соотношение
![]() .
(7)
.
(7)
Эти соотношения позволяют просто оценить правдоподобность полученных в эксперименте значений и и сопоставить значения для других поглотителей.
Таким образом, эта методика заключаются в следующем. Получить по измеренным последовательным значениям потока бета-частиц эмпирическую зависимость
![]() .
.
Определить по этой эмпирической функции значения толщин слоев, ослабляющих поток бета–частиц в 21, 22 и 23 раз. Найти значения на основе этих данных с помощью таблицы 3, рис.2, рис.3 номограммы рис.4 Приложения.
Преимущество этой методики по сравнению с методикой максимального пробега заключается в отсутствии большой погрешности определения значений , так как значения, например, d1/2 и d1/4, можно определить с меньшей погрешностью, поскольку значение функции ослабления J(d1/2), J(d1/4)много больше уровня фона и их можно легко оценить путем интерполяции экспериментальной зависимости .
2.3 Методика определения граничной энергии бета-спектра по коэффициенту ослабления потока бета-частиц
Ослабление бета-излучения в веществе, то есть функцию ослабления можно приближенно представить показательной функцией для нетолстых слоев поглотителя (в сравнении с пробегом бета–частиц – ):
![]() ,
(8)
,
(8)
где
–
интенсивность потока бета–частиц после
ослабления слоем вещества толщиной
,
![]() –
интенсивность потока до поглотителя,
–
линейный коэффициент ослабления.
Значения
убывают с увеличением максимальной
энергии бета-спектра. Величина
–
приблизительно пропорциональна плотности
вещества, поглощающего бета–частицы,
а отношение
–
интенсивность потока до поглотителя,
–
линейный коэффициент ослабления.
Значения
убывают с увеличением максимальной
энергии бета-спектра. Величина
–
приблизительно пропорциональна плотности
вещества, поглощающего бета–частицы,
а отношение
![]() ,
называемое массовым коэффициентом
ослабления, плавно растет с увеличением
отношения
,
называемое массовым коэффициентом
ослабления, плавно растет с увеличением
отношения
![]() .
Поэтому для не сильно отличающихся по
составу веществ, например, близких по
,
величина
приблизительно постоянна при данном
энергетическом бета-спектре, являясь
в тоже время функцией
.
Поэтому для не сильно отличающихся по
составу веществ, например, близких по
,
величина
приблизительно постоянна при данном
энергетическом бета-спектре, являясь
в тоже время функцией
![]() .
.
Вследствие этого
для различных веществ поглотителей
приблизительно можно получить единую
функцию ослабления интенсивности потока
бета-частиц
,
если за толщину слоя взять величину
массы вещества на единицу поверхности
![]() (г/см2).
Используя величину
(г/см2).
Используя величину
![]() функцию ослабления, можно записать в
виде
функцию ослабления, можно записать в
виде
![]() .
Очевидно, методика, основанная на
экспоненциальной модели ослабления
потока бета-излучения, является достаточно
простой экспериментальной методикой
определения значения максимальной
энергии бета-спектра.
.
Очевидно, методика, основанная на
экспоненциальной модели ослабления
потока бета-излучения, является достаточно
простой экспериментальной методикой
определения значения максимальной
энергии бета-спектра.
Таким образом,
методика определения
по значению коэффициента ослабления
потока бета-излучения заключается в
следующем:
по эмпирической
функции ослабления
в интервале значений толщин поглотителя,
где
![]() ,
где
,
где
![]() определяют два значения
определяют два значения
![]() ,
,
![]() (с учетом интенсивности фона) и вычисляют
коэффициенты ослабления по формулам
(9).
(с учетом интенсивности фона) и вычисляют
коэффициенты ослабления по формулам
(9).
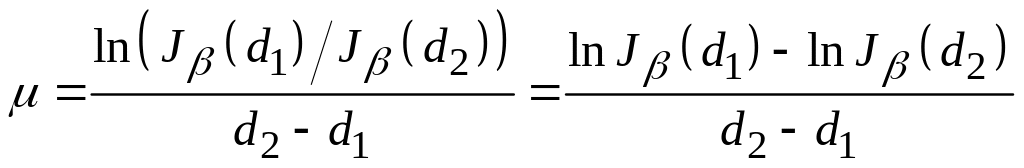 ,
см–1
(9)
,
см–1
(9)
где
![]() ,
,
![]()
![]() ,
,
(см2/г).
Величина
и слой половинного ослабления связаны
очевидным соотношением
![]() .
.
Кроме того, для
бета-частиц с
![]() МэВ справедливо эмпирическое соотношение
МэВ справедливо эмпирическое соотношение
![]() ,
откуда следует
,
откуда следует
![]() .
Эти соотношения следует использовать
в простых экспрессных оценках в процессе
опыта.
.
Эти соотношения следует использовать
в простых экспрессных оценках в процессе
опыта.
Необходимо
подчеркнуть, что экспоненциальная
модель ослабления бета-излучения
является весьма грубым приближением.
В частности при толщине поглотителя,
близкой к максимальному пробегу
,
логарифм функции ослабления стремится
к бесконечности рис.5 Приложения.
Экспоненциальная модель несостоятельна
при толщинах поглотителя, превышающих
0,3
,
когда поток бета-частиц убывает более
чем в два раза и на малых толщинах
![]() .
Лишь в интервале
.
Лишь в интервале
![]() функция
функция
![]() линейна. Поэтому определение
по формуле (9) необходимо проводить для
значений R
в интервале 0,05
–
0,3
.
линейна. Поэтому определение
по формуле (9) необходимо проводить для
значений R
в интервале 0,05
–
0,3
.
Отметим, что из-за приближенности модели экспоненциальной функции ослабления потока бета-излучения не имеет смысла определять при множестве значений .
Зависимость от Emax можно представить следующими формулами:
![]() см2/г,
см2/г,
где
![]() –
МэВ и соответственно:
–
МэВ и соответственно:
![]() МэВ. (10)
МэВ. (10)
Различия в значениях , полученные при использовании этих формул, связаны с зависимостью формы эмпирической кривой ослабления потока от условий измерений, (материала поглотителя, геометрии измерений).
Значение
![]() определяют по формуле (10), по графику
рис. 6 и таблице 3 в Приложении. Так как
каждый бета-радионуклид имеет только
соответствующее ему значение
а
есть однозначная функция от
,
то по найденному значению
можно прямо идентифицировать радионуклид
с помощью таблицы 5 Приложения. В таблице
6 даны характеристики нескольких веществ
поглотителей.
определяют по формуле (10), по графику
рис. 6 и таблице 3 в Приложении. Так как
каждый бета-радионуклид имеет только
соответствующее ему значение
а
есть однозначная функция от
,
то по найденному значению
можно прямо идентифицировать радионуклид
с помощью таблицы 5 Приложения. В таблице
6 даны характеристики нескольких веществ
поглотителей.
