
- •1.1.Регистрация и хранение измерительной информации. Интерполяционная формула Лагранжа.
- •1.2.Основные принципы построения автоматизированных си и контроля.
- •1.3.Государственная система обеспечения единства измерений (гси).
- •11.1.Согласование сигнала с каналом связи. Теорема Шеннона с предельной пропускной способностью канала.
- •11.2 Основные цели и объекты сертификации. Термины и определения в области сертификации продукции. Защита прав потребителя.
- •Объекты сертификации:
- •11.3 Калибровка си. Организация и порядок проведения
- •12.1 Полные и динамические характеристики си
- •12.2Функция преобразования и ее числовые характеристики.
- •12.3 Органы и службы стандартизации
- •13.1 Стационарные и нестационарные режимы работы средств измерений.
- •13.2 Метрологическое обеспечение. Основные цели и задачи.
- •13.3 Построение, содержание и изложение стандартов. Информация о документах по стандартизации.
- •14.1 Режимы работы средств измерений. Установившийся режим. Переходный режим
- •14.2 Управление качеством на этапе производства. Метод Тагути.
- •Особенности метода
- •Достоинства
- •Недостатки
- •Ожидаемый результат
- •14.3 Стандартизация технической документации. Основные межотраслевые системы, их состав и общая характеристика.
- •15.1.Нормируемые метрологические характеристики си. Примеры.
- •15.2 Гсс рф. Основные стандарты. Общие положения.
- •15.3.Объекты и компоненты мо. Производство как объект мо. Особенности мо на различных стадиях производства.
- •16.2 Автоматизированные средства измерений с одно- и двукратным сравнением
- •Средства измерений с двукратным сравнением
- •16.3. Международная стандартизация. Деятельность международных организаций по стандартизации. Международные стандарты и их применение
- •17.3 Ряды предпочтительных чисел и их применение
- •7.3. Международные организации по стандартизации
- •Глава 7. Основы государственной системы стандартизации 2ш
- •17.1 Передача информации о размерах единиц
- •2. Методика выполнения измерений (мви). Разработка, аттестации и надзор за применением мви.
- •26.1.Аксиомы метрологии. Математические модели эмпирических зрв.
- •26. 2. Применение средств вычислительной техники в си.
- •26.2 Применение вычислительной техники в средствах
- •26. 3. Измерение качества. Структура показателей качества.
- •27. 1. Измеряемые величины, их качественная и количественная характеристики.
- •27. 2. Применение си физической величины (по выбору).
- •Принцип действия
- •Способы подключения
- •Применение термопар
- •Преимущества термопар
- •Недостатки
- •Типы термопар
Билет 1
1.1.Регистрация и хранение измерительной информации. Интерполяционная формула Лагранжа.
В зависимости от характера ее дальнейшего использования измерительная информация может запоминаться на непродолжительное или продолжительное время, может предъявляться получателю в форме, удобной для ее восприятия, или регистрироваться в виде рабочего или официального документа.
Примером запоминания на непродолжительное время измерительной информации о быстропротекающем процессе, представленной в аналоговой форме, является осциллограмма этого процесса на экране электронно-лучевой трубки с длительным послесвечением. В цифровой форме измерительная информация запоминается на непродолжительное время в оперативных запоминающих устройствах (ОЗУ) современных ЦЭВМ, а на продолжительное время — во внешней памяти этих машин.
В качестве цифровых запоминающих элементов ОЗУ наибольшее распространение получили триггеры и ферритовые сердечники, обладающие двумя устойчивыми состояниями, т.е. способные хранить один двоичный разряд (0 или 1) числа. Кроме того, могут использоваться различные физические или химические явления.
При применении триггера в качестве запоминающего элемента одно из его состояний принимается за 1, а другое — за 0. Во многих схемах при этом используется только один из выходов триггера.

Цепочку триггеров, соединенных последовательно (см. рис. 186), можно использовать как регистр для запоминания двоичного числа с количеством разрядов, равным числу триггеров. В этом случае триггеры имеют дополнительные входы (С) для подачи "сдвигающих" импульсов, тактирующих работу триггеров.
Предположим, что в исходном состоянии со всех триггеров снимаются нули (двоичное число 0000), и в регистр нужно ввести число 1011, заданное в виде соответствующей последовательности импульсов на основном входе триггера Тг4 старшего разряда. Последовательность работы регистра в этом случае будет следующая. Первый входной импульс перебрасывает Тг4, на выходе которого устанавливается 1, но возникающий при этом перепад потенциалов не воздействует на Тг3. В регистре зафиксировано число 1000. После этого поступает тактовый импульс сдвига, перебрасывающий Тг4 в исходное состояние (0) и за счет этого перебрасывающий Тг3 на 1. Произошел сдвиг числа на один разряд вправо, и в регистре зафиксировано число 0100. Далее процесс протекает аналогично. Следующий входной импульс записывает 1 в Тг4 (на регистре число 1100), а следующий импульс сдвига сдвигает это число на разряд вправо, т.к. сбрасывает единицы с Тг4 и Тг3 и переносит их в Тг3 и Тг2 (на регистре число 0110). Так как в этом случае Тг3 одновременно должен и сбросить единицу от импульса сдвига и записать единицу от Тг4, необходимо несколько задержать импульс от Тг4, что осуществляется засчет собственных задержек Д-триггеров. Следующий входной импульс отсутствует и состояние регистра не меняется, а следующий импульс сдвига сдвигает записанное в нем число на разряд вправо (в регистре число 0011). Последний входной импульс записывает в Тг4 единицу, и процесс ввода заканчивается (в регистре число 1011).
Записанное число можно вывести параллельно непосредственно с триггеров и последовательно с выхода регистра путем подачи серии импульсов сдвига в количестве, равном числу разрядов регистра; можно сдвинуть вправо на количество разрядов, равное количеству поданных импульсов сдвига.
При параллельном вводе записываемого числа разрядные импульсы подаются на соответствующие триггеры одновременно. В этом случае импульсы сдвига используются только при необходимости последовательного вывода записанного числа, а параллельный вывод числа производится через не тактируемые установочные (S-R) входы Д-триггеров.
Возможны и другие варианты построения схем регистров.
Внешняя память ЦЭВМ бывает в самом разнообразном исполнении: на магнитных лентах, барабанах, дисках и т.п.
Предъявление измерительной информации потребителю в форме, удобной для восприятия, осуществляется обычно с помощью цифровых индикаторов. Во многих случаях они представляют собой световое табло.
Регистрация измерительной информации в аналоговой форме производится с помощью светолучевых осциллографов, самописцев, графопостроителей и т.п. устройств.
Записанная на бумажном носителе измерительная информация первоначально представляет собой рабочий документ. Для приобретения статуса официального документа она должна пройти метрологическую экспертизу.
При метрологической экспертизе устанавливается точность, правильность и достоверность измерительной информации. Прошедшая метрологическую экспертизу измерительная информация приобретает статус информационных данных и может включаться в отчеты или представляться для опубликования в печати.
Интерполяционная формула Лагранжа.
З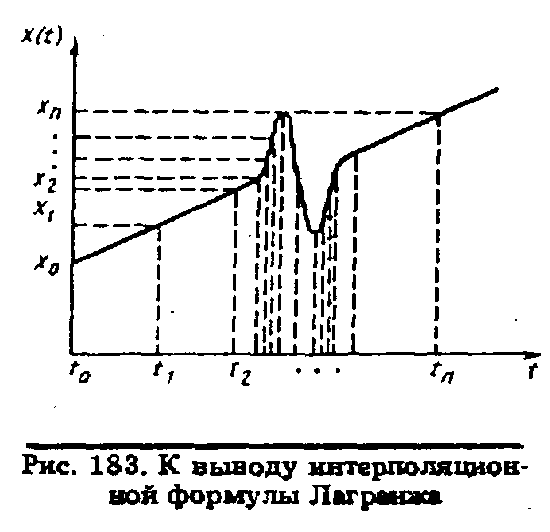 адача
- восстановления сигнала с помощью
полинома n-й
степени ставится следующим образом.
Пусть известны значения сигнала 0,
X1,
Х2
, . .. Хn
в моменты времени t0
,t1
,t2
, ... , tn
(см.
рис. 183). Требуется найти такой непрерывный
сигнал Х(t),
который в моменты времени tj
принимал бы значения XJ
.
адача
- восстановления сигнала с помощью
полинома n-й
степени ставится следующим образом.
Пусть известны значения сигнала 0,
X1,
Х2
, . .. Хn
в моменты времени t0
,t1
,t2
, ... , tn
(см.
рис. 183). Требуется найти такой непрерывный
сигнал Х(t),
который в моменты времени tj
принимал бы значения XJ
.
Найдем прежде всего непрерывную функцию, принимающую значение 1 в момент времени t0, и равную нулю во все остальные моменты времени ti. Легко проверить, что такой функцией будет дробь
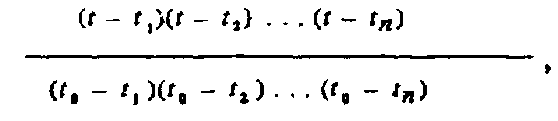
в которой при t = t0 числитель и знаменатель оказываются совершенно идентичными, а в любой другой момент времени ti, один из сомножителей в числителе обращается в ноль. Домножив эту функцию на Х0, получим непрерывный сигнал
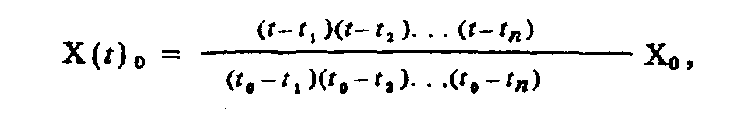
принимающий значение Х0 в момент времени t0 , и равный нулю во все остальные моменты времени ti .
Поступая по аналогии, можно сформировать сигналы
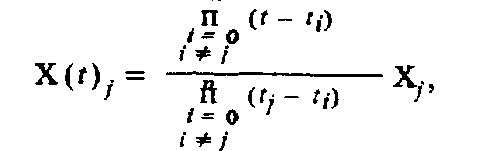
принимающие значения Xj в моменты времени tj, и равные нулю во все остальные дискретные моменты времени ti ≠ tj . Искомый сигнал Х(t) будет равен сумме этих сигналов
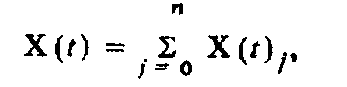
так как в каждый из моментов времени tj принимает значение Xj.
Формула

называется интерполяционной формулой Лагранжа и представляет собой полином n-й степени. На практике обычно интерполируют сигнал между двумя соседними дискретными значениями. В этом случае п = 1, и интерполяционный полином имеет вид
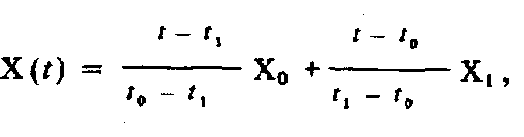
или, после преобразований,
![]()
![]()
где
а =
![]() ;
b=
;
b=![]() .
Это уравнение прямой,
.
Это уравнение прямой,
проходящей через точки с координатами (t0,Xо) и (t1,Xi). Такая интерполяция называется линейной. Пример восстановления сигнала методом линейной интерполяции показан на рис. 184.
При степени полинома п = 0 интерполяция фактически превращается в экстраполяцию, так как в этом случае
![]()
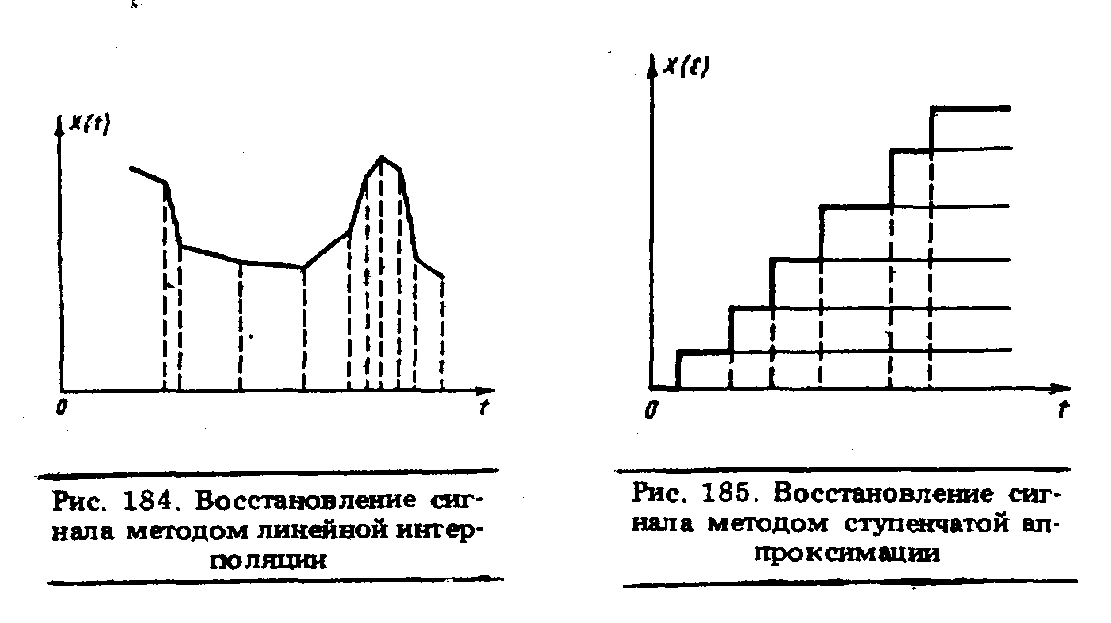
Пример восстановления сигнала таким способом в каждый дискретный момент времени tj .показан на рис. 185. В измерительной технике этот способ восстановления реализуется с помощью разнообразных преобразователей код—аналог.
