11. Принятие решения о качестве факторной структуры

Формальное требование к факторной структуре называется принципом простой структуры. Это выражается в том, что каждая переменная имеет близкие к нулю нагрузки по всем факторам, кроме одного.

В настоящее время не существует формальных критериев простоты факторной структуры. Основным критерием является возможность содержательной интерпретации фактора по двум и более исходным переменным.

Разработаны подходы приближения к простой структуре путем пошагового сокращения факторов и переменных.

1. Если выявлен фактор, по которому ни одна из переменных не получила существенно большей (по сравнению с другими факторами) нагрузки, то стоит уменьшить число факторов.

2. Если фактор идентифицируется только по одной переменной. А остальные не вошли в него даже с второстепенными нагрузками, то стоит уменьшить число факторов.

3. Если имеются неоднозначные переменные, то есть переменные, которые имеют примерно одинаковые по модулю факторные нагрузки по двум и более факторам, то эти переменные следует поочередно удалять из исследования.

12. Вычисление оценок факторов

Оценки факторных нагрузок являются коэффициентами линейного уравнения, связывающего значения факторов и значения исходных переменных. Они показывают, с каким весом входят исходные значения каждой переменной в оценку факторов. Факторные коэффициенты можно использовать для вычисления факторных оценок для новых объектов, не включенных ранее в факторный анализ.

Факторные оценки – значения факторов для конкретного объекта. Факторные оценки отражают структуру взаимосвязей исходных признаков

13. Задачи, решаемые с использованием факторного анализа

С появлением специализированных пакетов статистической обработки информации появилась возможность широкого применения факторного анализа при решении исследовательских и практических задач:

1. Факторный анализ позволяет выделять группы взаимосвязанных переменных.

2. Факторный анализ позволяет сократить исходное множество признаков до нескольких факторов, которые отражают разные стороны исследуемого объекта.

3. Факторный анализ позволяет оценивать количественно комплексные характеристики объектов, учитывая реальную структуру и взаимосвязь исходных переменных, избегая потерь информации и оценивания путем простого суммирования.

4. Результаты факторного анализа могут быть использованы для последующего регрессионного, дискриминантного и кластерного анализа.

14. Факторный анализ в spss

14.1. Вызов процедуры

Вызов процедуры осуществляется командами Analyze/ Data Reduction/ Factor…(рис.14-1)

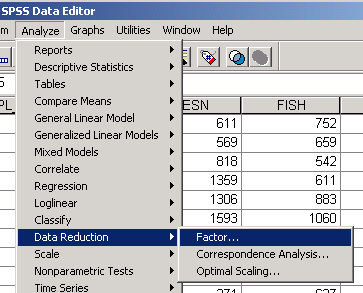
Рис.14-1. Вызов процедуры факторного анализа

Установка параметров метода главных компонент производится в нескольких диалоговых окнах. После вызова процедуры откроется соответствующее меню (рис.14-2). В диалоговом окне имеется несколько кнопок, нажатие каждой из которых открывает свое диалоговое окно.

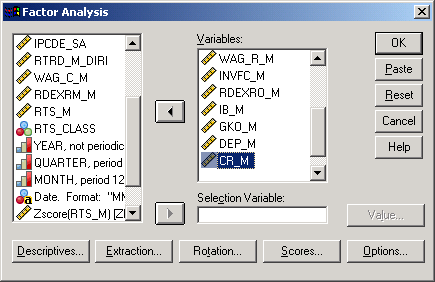
Рис.14-2. Вид окна Factor Analysis

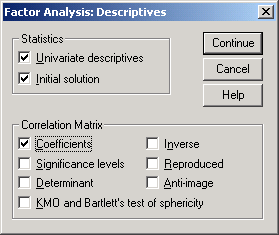
Рис.14-3. Вид окна Factor Analysis: Descriptives

В окне Factor Analysis: Descriptives имеются следующие возможности:

• Univariate descriptives  определение количества значащих наблюдений, математическое ожидание и стандартное отклонение по каждой исходной переменной.

• Initial solution  отображение исходных общностей Communalities и процента объясненной дисперсии. Для каждой переменной общность  это доля дисперсии данной переменной, которая может быть объяснена факторами (компонентами). Естественно, изначально доля объясненной дисперсии переменной тождественно равна единице, поскольку факторы-компоненты тождественно равны переменным. В рассмотренном ниже случае SPSS выделил две компоненты, поэтому оценки общностей в следующем столбце сообщают долю дисперсии переменной, объясненной этими двумя факторами.

• Coefficients  получение матрицы корреляции между исходными переменными Х₁ … Х_К.

Метод главных компонент предполагает анализ матрицы корреляции Correlation matrix между Х1 … ХК. Те переменные, которые имеют высокую степень корреляции, будут объединены в компоненты.

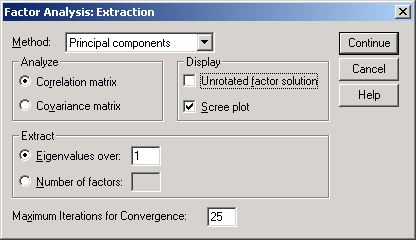
Рис.14-4. Вид окна Extraction

Scree plot  график типа "осыпь" с собственными значениями переменных по оси ординат и их порядковыми номерами по оси абсцисс. График можно использовать для выбора числа факторов или порогового собственного значения, поскольку он наглядно отражает различие между большими и маленькими собственными значениями (рис.14.5).

По умолчанию, SPSS отбирает компоненты с собственными значениями Eigenvalue, превосходящими 1. Можно самостоятельно задать пороговое значение или количество компонент (вне зависимости от собственных значений).

Опция Rotation (Окно Factor Analysis: Rotation ) применяется с тем, чтобы полученные результаты было легче интерпретировать. SPSS осуществляет вращение векторов так, чтобы каждой исходной переменной соответствовало наименьшее количество компонент. В SPSS реализовано несколько методов вращения. Например, Varimax  метод ортогонального вращения, который облегчает интерпретацию компонент.

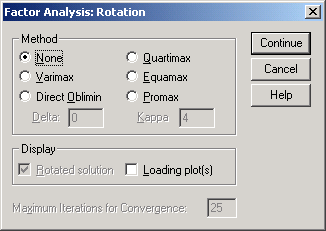
Рис.14-6. Вид окна Rotation

Loading plot (Окно Loading Plot)  график компонент в повернутом пространстве. Координатами точек этого графика являются нагрузки трех первых компонент. Чем ближе какая-либо координата к нулю, тем слабее переменная ассоциируется с данной компонентой (рис.14-7).

В диалоговом окне Factor Analysis: Scores (рис. 14.8) можно установить опцию о том, чтобы выделенные компоненты были вычислены и сохранены как новые переменные. После проведения анализа методом главных компонент, на них можно построить регрессию. Обратим внимание – для дальнейшего проведения процедуры регрессия на главных факторах, необходимо поставить флажок Display factor Score coefficient matrix.

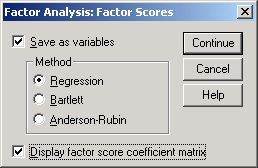
Рис.6-8. Вид диалогового окна Factor Analysis: Scores

14.2. Вид результатов расчета главных компонент

Результаты расчета главных компонент представлены в нескольких таблицах. Прокомментируем некоторые из них.

6.2.4.1. Корреляционная матрица (рис.6-9)

Рис.6-9. Вид корреляционной матрицы

Корреляционная матрица (рис.6-9) выглядит традиционно: на пересечении строки и столбца находится значение коэффициента корреляции между этими переменными. По значению и знаку судят о степени и направлению влияния одной переменной на другую.

6.2.4.2. Таблица Total Variance Explained (рис.6-10)

В этой таблице приводятся проценты общей вариации, объясняемой каждым фактором. Так 1- фактор объясняет 71,086% вариации; 2-й из оставшихся 28,914% объясняет 15,514% (итого вместе два первых фактора объясняют 86,6%).

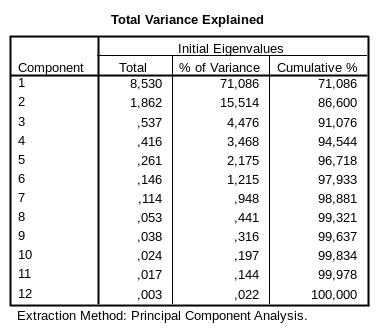
Рис.6-10. Вид таблицы Total Variance Explained

В зависимости от предъявляемой пользователем точности расчетов, из этой таблицы выбирается число факторов, которые необходимо учесть при дальнейших расчетах.

6.2.4.3. График Scree Plot (рис.6-11)

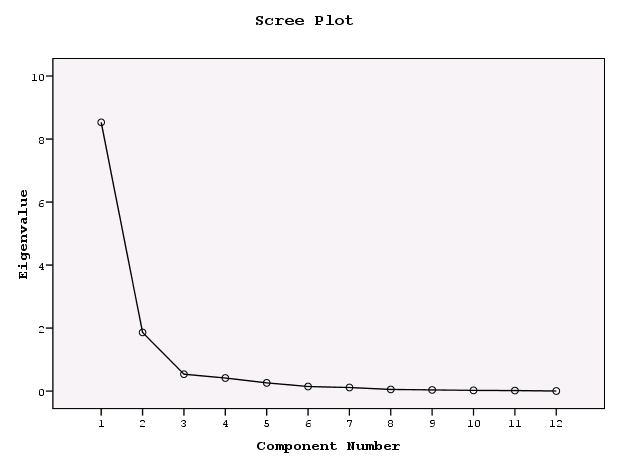
Рис.6-11. График процентов вариации, объясняемой каждым фактором

График Scree Plot представляет собой графическое изображение таблицы Total Variance Explained.

6.2.4.4 Таблица Score Coefficient Matrix (рис.6-12)

Результаты этой таблицы могут понадобиться при дальнейших расчетах регрессии на главных факторах. В ней приводятся нагрузки каждой переменной в нескольких главных факторах. Так, в 1-ом факторе переменная EMPLDEC имеет вес 0,102; переменная IMQ – вес 0,108 и т.д.

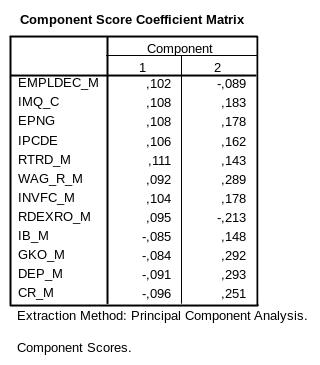
Рис.6-12. Таблица весов переменных в 2-х первых факторах

6.2.4.5. Таблица Component Score Covariance Matrix (рис.6-13)

В таблице приведена степень влияния между новыми переменными (главными факторами). Обратите внимание, что компоненты выбираются из условия, что они линейно независимы и отражают максимально возможную дисперсию, содержащуюся в исходных данных.

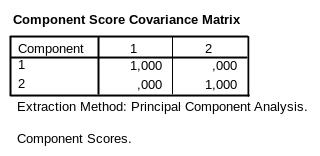
Рис.6-13. Независимость компонент друг от друга

6.3. Факторный анализ. Метод максимального правдоподобия с косоугольным вращением

6.3.1. Вызов процедуры

Вызов процедуры осуществляется командами:

Analyze

Data Reduction

Factor…(рис.6-1).

6.3.2. Установка параметров

В диалоговом окне Factor Analysis (рис.6-2) чтобы использовать те же исходные данные щёлкните на Reset, чтобы восстановить значения по умолчанию, и выберите в области Variables переменные.

В окне Factor Analysis: Descriptives можно оставить предыдущие параметры.

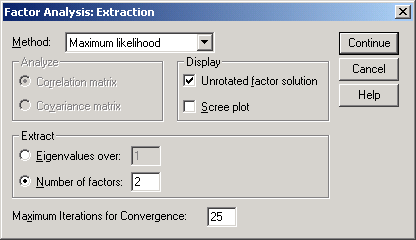
Рис.6-14. Установка метода максимального правдоподобия

В окне Factor Analysis: Extraction (рис.6-14) в поле Method установите Maximum likelihood (метод максимального правдоподобия).

В области Extract активизируйте Number of factors: 2 (два фактора)…

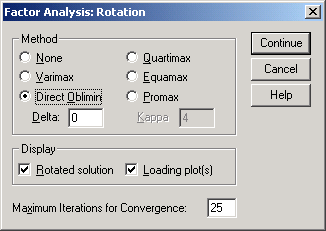
Рис.6-15. Установка параметров в окне Factor Analysis: Rotation

В окне Factor Analysis: Rotation (Вращение) в области Method активизируйте Direct oblimin (рис.6-15).

В области Display активизируйте (рис.6-15) Loading plot(s) и Rotated solution.

В окне Factor Analysis: Factor Scores (рис.6-16) активизируйте Save as variables (Сохранить как переменные).

В окне Factor Analysis: Options (рис.6-17) в области Coefficient Display Format активизируйте кнопки Sorted by size и Suppress absolute values less than: 0,20.

6.3.3. Результаты расчета

Результаты факторного анализа представлены в виде таблиц общностей (рис.6-18) и объясненной дисперсии (рис.6-19).

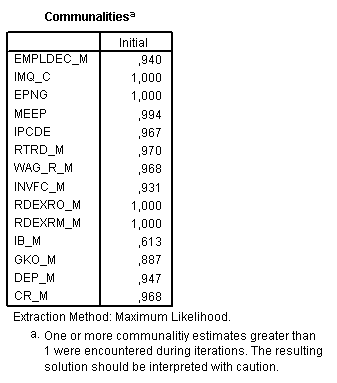
Рис.6-18. Таблица общностей

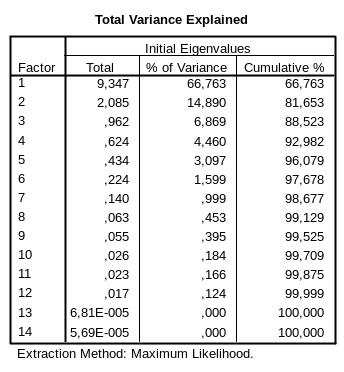
Рис.6-19. Таблица объясненной дисперсии

6.3.3.1. Таблица общности

Общности (рис.6-18) выводятся до выделения факторов. Для каждого метода выделения, за исключением метода главных компонент, оценка, размещающаяся в столбце Initial (Начальная), равняется множественному R-квадрат (коэффициенту детерминации) с переменной текущей строки в качестве зависимой и всеми остальными в качестве независимых переменных. Начальные общности используются в вычислениях при выделении факторов.

По умолчанию, даже при использовании метода максимального правдоподобия, для определения числа факторов используется метод главных компонент. Чтобы иметь возможность сравнить полученные результаты в методе максимального правдоподобия с результатами из примера 1, мы в качестве параметра установили выделение двух факторов (рис.6-14).

Общность для переменной IBM мала, так что она имеет слабое отношение к обоим факторам.