3.3. Ряды распределения

Одним из видов структурной группировки является ряд распределения. Элементами распределения являются варианты (названия или количественные выражения группировочного признака) и частоты (численность единиц, относящихся к каждой группе). Ряд распределения выглядит следующим образом

Варианты числового значения признака Х или наименования групп	Частоты (число наблюдений) или частости повторения значений признака, (f)
Х1	f1
Х2	f2
…	…
Хn	fn
Итого

Ряды распределения, построенные по признакам, измеренным в номинальной или порядковой шкале, называются атрибутивными. Ряды распределения, построенные по признакам, измеренным в количественных шкалах (интервальная шкала и шкала отношений), – вариационными.

Количественные признаки могут выражаться дискретными или непрерывными величинами. Соответственно, и вариационный ряд будет либо дискретным, либо интервальным (т.е. непрерывным в пределах интервала). Так, количество детей в семье может выражаться только целыми числами, а доход одного человека может отличаться от дохода другого на величину, определяемую точностью измерения (коп., руб., тыс.руб).

При построении вариационного ряда непрерывного признака совокупность распределяется по интервалам его значений. Интервалы можно брать как равные, так и неравные. Для каждого интервала указывается частота или частость, т.е. абсолютное или относительное число единиц, у которых значение признака находится внутри данного интервала.

Первый и последний интервалы ряда чаще всего берутся открытыми. Использование открытых интервалов удобно, когда в совокупностях встречается незначительное число единиц или с очень малыми, или очень большими значениями вариантов, резко отличающимися от всех остальных значений.

Если построен ряд с равными интервалами, то частоты дают представление о том, как заполнен единицами совокупности тот или иной интервал. Для сравнения частот ряда (с равными и, особенно, неравными интервалами) используется характеристика плотности распределения. Плотность в интервале – это частное от деления частоты или частости на величину интервала; в первом случае получается абсолютная, во втором – относительная плотность распределения. Плотность показывает, сколько единиц (сколько процентов единиц или какая часть) совокупности приходится в среднем на единицу изменения признака в данном интервале.

Для характеристики распределения используют также абсолютные накопленные частоты или накопленные относительные частости. Накопленная частота (частость) для данного дискретного варианта или для верхней границы данного интервала получается суммированием (накапливанием) частот или частостей во всех предшествующих интервалах, включая данный,. Накопленная частота (частость) показывает, какое число или какая доля единиц совокупности имеет значение признака, не превышающее данного дискретного варианта или верхней границы интервала.

Зависимость частот, или, точнее, плотностей распределения от величины группировочного признака может быть представлена некоторой функцией, изображаемой графически кривой определенного вида и воспроизводящей основные особенности распределения изучаемого показателя. В зависимости от вида кривых, изображающих это распределение, выделяют несколько основных типов. Распределения по виду их графического изображения можно разделить на одновершинные и многовершинные. К одновершинным относятся распределения, в которых один, обычно центральный, вариант имеет наибольшую частоту (точнее, наибольшую плотность распределения), частоты же остальных вариантов убывают по мере удаления от центрального. Если частоты убывают одинаково и справа, и слева от центрального значения, то такие распределения называются симметричными. Если частоты убывают от центра распределения с разной интенсивностью, то такие распределения называют асимметричными, выделяя при этом распределения, растянутые вправо или влево. Степень асимметрии может быть различной, от совершенно незначительной до такой, при которой наибольшая частота признака X обнаруживается в одном из крайних вариантов значений.

Идеальное симметричное распределение крайне редко встречается на практике. Основная масса распределений, с которыми приходится иметь дело экономисту, это асимметричные распределения с разным видом и степенью асимметрии. Примером явной правосторонней асимметрии может опять-таки служить распределение населения по уровню денежного дохода.

Многовершинные распределения – это распределения, у которых несколько максимумов частот (несколько центров). Многовершинность распределения часто является свидетельством того, что совокупность состоит из неоднородных, с точки зрения изучаемого признака, единиц. Поэтому, убедившись в том, что распределение имеет более, чем один максимум частот, исследователь должен тщательно проверить, можно ли считать однородными единицы такой совокупности.

В практической деятельности очень важно фактическое распределение (фактическую структуру совокупности) привести к виду, известному теоретически. Обычно в экономических расчетах аппроксимируют к следующим теоретическим плотностям распределения (плотностям вероятности) значений признака X.

Нормальное

После подстановки функция плотности нормального распределения вероятностей принимает вид¹

.

Логарифмически нормальное. Функция плотности распределения имеет вид

где

т.е. среднее значение логарифмов признака Х,

среднее квадратическое отклонение логарифмов значений² признака X.

Равномерное. Функция плотности вероятности имеет одинаковое значение в каждом из k интервалов –

Показательное –

Для показательного распределения характерно, что среднее значение признака равно его среднему квадратическому отклонению.

Распределение Пуассона (для дискретных распределений Х) –

.

Распределение Пуассона оценивает вероятность появления заданного числа (x) достаточно редких событий. Параметр a – это математическое ожидание (среднее значение) числа событий в данных обстоятельствах.

Представив фактическую структуру одним из типов вероятностных распределений, следует ответить на вопрос, действительно ли различия между теоретической и эмпирической кривой плотности распределения настолько малы, что их можно считать случайными, а не закономерными. Наиболее известный метод проверки соответствия фактического ряда распределения теоретическому – это применение критерия согласия χ² Пирсона. Определяем величину

.

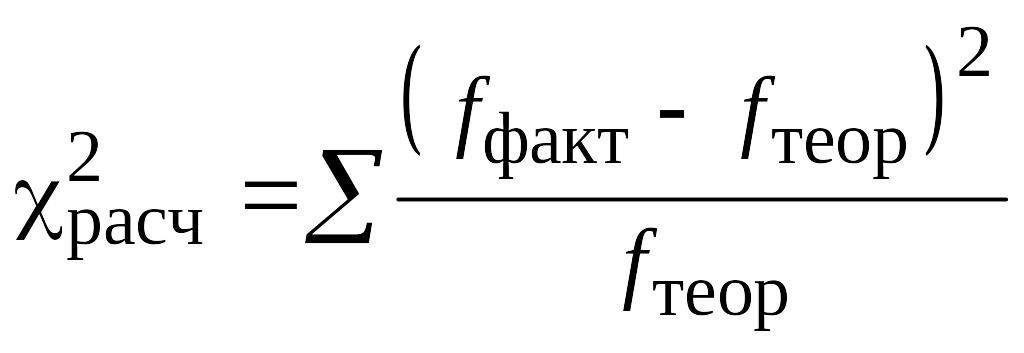Сравниваем χ²_расч. с χ²_табл. при заданном уровне значимости (α) и числе степеней свободы (ν). Если, χ²_расч.<χ²_табл, можно считать, что фактическое распределение адекватно теоретическому.

Пример. Имеется следующий интервальный ряд распределения по уровню заработной платы:

Заработная плата, тыс.руб./чел.	Число рабочих
До 2,0	10
2,0 – 2,5	20
2,5 – 3,0	40
3,0 – 3,5	20
3,5 и более	10
Итого	100

Предполагая, что распределение рабочих по уровню заработной платы является нормальным, рассчитаем теоретические частоты.

Середины интервалов	fфакт		x·fфакт	(x)2fфакт		f(t)	fтеор = f(t)K= f(t)91,29	Округленные теоретические частоты
1,75	10	–2	–20	40	–1,823	0,07573	6,947	7
2,25	20	–1	–20	20	–0,913	0,26297	24,073	24
2,75	40	0	0	0	0,0	0,39894	36,416	37
3,25	20	1	20	20	0,913	0,26297	24,073	24
3,75	10	2	20	40	1,823	0,07573	6,947	7
Итого	100	0	0	120		1,07634		99

В расчетной таблице f(t) это плотность нормального распределения. Для ее определения используются либо специальные вероятностные таблицы, либо непосредственно формула плотности, приведенная выше. Рассчитаем среднее значение признака и его среднее квадратическое отклонение методом моментов, где центральный момент А = 2,75, а величина интервала i = 0,5.

;

Таким образом ;

.

K – поправочный коэффициент³:

;

χ²_табл (α=0,05; ν=k-r-1=5-2-1=2) = 5,991.

Здесь  – уровень значимости; ν –число степеней свободы; k – число групп; r – число параметров распределения. Имеем χ²_расч.<χ²_табл, следовательно, распределение является нормальным.