
- •2. Элементарные крывыя
- •3.Агульныя крывыя
- •5.Параметрычны спосаб задання элементарных крывых
- •6.* Параметрычны спосаб задання агульных крывых.
- •7*. Гладкія(рэгулярныя) элементарныя урывыя. Эквівалентныя параметрызацыі.
- •9*. Яўнае заданне прасторавай крывой ў дэкартавых каардынатах
- •10.Няяўнае заданне плоскай крывой у дэкартавых каардынатах.
- •11*.Няяўнае заданне прасторавай крывой ў дэкартавых каардынатах.
- •12*. Заданне крывых у недэкартавых каардынатах.
- •13. Датычная прамая крывой.
- •15.Нармальная плоскасць прасторавай крывой.
- •16*.Вугал паміж крывымі.
- •17.Даўжыня дугі крывой
- •18.Формулы для вылічэння даўжыні дугі.
- •19**.Натуральная параметрызацыя крывой
- •21.Суправаджальны трохграннік прасторавай крывой.
- •22.Кананічны базіс і рухомы рэпер
- •23*.Формулы Фрэнэ
- •24. Крывізна і кручэнне крывой
- •29.Крывая нулявога кручэння.Пункты сплашчэння
- •30*.Асноўная тэарэма тэорыі крывых
22.Кананічны базіс і рухомы рэпер
Правая
тройка адзінкавых вектароў
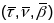 ,
дзе
,
дзе
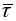 – орт датычнай прамой Т,
– орт датычнай прамой Т,
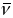 - орт галоўнай нармалі N,
- орт галоўнай нармалі N,
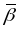 - орт бінармалі В, называецца кананічным
базісам крывой
(у пункце Р).
- орт бінармалі В, называецца кананічным
базісам крывой
(у пункце Р).
Відавочна, што вуглы паміж парамі вектароў кананічнага базісу прамыя і мае месца ф-ла:
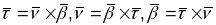
Чацверка
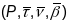 ,
дзе
,
дзе
 пункт
крывой
і кананічныя в-ры ў ім наз рухомым
рэперам крывой
у яе пункце Р
.
пункт
крывой
і кананічныя в-ры ў ім наз рухомым
рэперам крывой
у яе пункце Р
.
Узнікае
пытанне: як знайсці вектары
 ведаючы параметрызацыю крывой
.
Магчымы два выпадкі:
ведаючы параметрызацыю крывой
.
Магчымы два выпадкі:
1.
Няхай Крывая
задаецца натуральнай параметрызацыяй
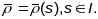

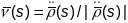 ,
,
 .
.
Першая
формула вынікае з таго, што
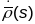 кіроўны вектар датычнай прамой Т, і
акрамя таго
кіроўны вектар датычнай прамой Т, і
акрамя таго
 ,
паколькі
,
паколькі
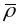 - натуральная параметрызацыя. Другая
формула выконваецца таму, што па-першае
- натуральная параметрызацыя. Другая
формула выконваецца таму, што па-першае
 ,
па-другое
,
па-другое
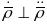 (паколькі
(паколькі




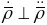 ).
).
2.
 – заданне крывой
,
наступныя вектары з’яўляюцца, відавочна,
кіроўнымі вектарамі Т, В, N
адпаведна:
– заданне крывой
,
наступныя вектары з’яўляюцца, відавочна,
кіроўнымі вектарамі Т, В, N
адпаведна:
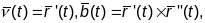
 ,
,
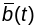 - кіроўны вектар бінармалі В,
- кіроўны вектар бінармалі В,
 - кіроўны вектар галоўнай нармалі N
у пункце Р(t)
(з параметрам t).
Нармуючы гэтыя вектары знойдзем вектары
кананічнага базісу у кожным адпаведным
пункце:
- кіроўны вектар галоўнай нармалі N
у пункце Р(t)
(з параметрам t).
Нармуючы гэтыя вектары знойдзем вектары
кананічнага базісу у кожным адпаведным
пункце:
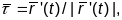
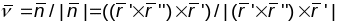 ,
,
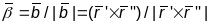
23*.Формулы Фрэнэ
24. Крывізна і кручэнне крывой
З фармальнага пункта гледжання крывізна k і кручэнне ᴂ каэф-ен ў правых частках формулы Франэ
K імгненная хуткасць датычнай прамой Т
ᴂ-гэта імгненная хуткасць вярчэння нармалі β
Будзе паказана, што і k і ᴂ два галоўных інварыянта, якія цалкам вызначаюць уласцівасці крывой. Будзе паказана, што яны вылічваюцца па ф-ле:
K(t)= ; ᴂ=
; ᴂ=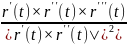 у пункце Р(t)
параметрызаванай
крывой (γ,r)
у пункце Р(t)
параметрызаванай
крывой (γ,r)
Крывізна
k
і кручэнне ᴂ
былі уведзены фармальна , як адпаведныя
каэфіцыены у ф-лах Франэ:
 .
.
 і
і
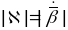 .
.
Вынік:
1. Крывізна k - неадмоўная велічыня;
2.
Кручэнне
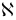 - можа прымаць як адмоўнае, так і дадатнае
і нулявое кручэнне у пункце крывой:
- можа прымаць як адмоўнае, так і дадатнае
і нулявое кручэнне у пункце крывой:
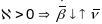 ,
,
 ,
,
 .
.
25**.Вылічэнне крывізны
26**.Вылічэнне кручэння
27.Крывізна і кручэнне акружнасці, графіка функцыі, шрубавай лініі
Вынік: Крывізна акружнасці радыуса R адваротна прапарцыйнаму яе радыусу, а кручэнне яго радыуса рощнае нулю.
Заўвага: Можна было таксама вылічыць k і ᴂ акружнасці, выкарыстоўваючы ф-лы k(t)= ; ᴂ=
Увёўшы сіс-му каардынат Оху у пл-ці акружнасці і параметрызаваўшы яе.
28.Крывая нулявой крывізны. Пункты спрамлення
Сцв.
Крывая
класа
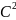 крывізны к, якая
крывізны к, якая
Ёсць прамая ці яе частка.
Адваротнае таксама верна.
Доказ: Калі ρ=ρ(s), s∈J натуральная параметрызацыя крывой γ, для якой k≠0, маем:
Усе разважанні адбрасываюцца
Пункт гладкай крывой, у якім k=0 наз. Пунктам спрамлення, выспрасавання
Адпаведная т-ме прамая цалкам складаецца з пунктаў выпрасавання.
На іншых крывых пунктаў выпрасавання могуць распалагацца ізаліравана ці ўвогуле адсутнічаць. Напрыклад, акружнасць ці шрубавая лінія
Калі знайсці пункт выпрасавання гладкай крывой, дастаткова вырашыць раўнанне: k=0
 ,
,
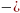 адвольная
параметрызацыя крывой
k=
адвольная
параметрызацыя крывой
k=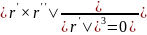
 Крывая
класа
Крывая
класа
 з’яўляецца бірэгулярнай калі і толькі
калі, на ёй няма пунктаў спрамлення.
з’яўляецца бірэгулярнай калі і толькі
калі, на ёй няма пунктаў спрамлення.
