Линейная Агебра

vk.com/club152685050 | vk.com/id446425943

6)х2 — 2ху + у2 — 6х + 6у — 3 = 0;

7)4х2 — 20ху + 25у2 — 14х + 2у — 15 = 0;

8)4х2 — 6ху — 9у2 + 3х — 7у + 12 = 0.

666.Установить, что следующие линии являются центральными, и для каждой из них найти координаты центра:

1)3х2 + 5ху +y2 — 8х — 11у — 7 = 0;

2)5х2 + 4ху + 2y2 + 20х+ 20у — 18 = 0;

3)9х2 — 4ху — 7y2 — 12 = 0;

4)2х2 — 6ху + 5у2 + 22х — 36у + 11 = 0.

667.Установить, что каждая из следующих линий имеет бесконечно много центров; для каждой из них составить уравнение геометрического места центров:

1)х2 — 6ху + 9y2 — 12х + 36y + 20 = 0;

2)4х2 + 4ху + у2 — 8х — 4у — 21 = 0;

3)25x2 — 10ху + у2 + 40х — 8у + 7 = 0.

668.Установить, что следующие уравнения определяют центральные линии; преобразовать каждое из них путём переноса начала координат в центр:

1)3х2 — 6ху + 2у2 — 4х + 2у+1=0;

2)6х2 + 4ху +y2 + 4х — 2у + 2=0;

3)4х2 + 6ху+у2 — 10х —10 = 0;

4)4х2 + 2ху + 6y2 + 6х — 10у + 9 = 0.

669.При каких значениях т и п уравнение

mх2 + 12ху + 9у2 + 4х + пу — 13 = 0

определяет:

а) центральную линию; б) линию без центра;

в) линию, имеющую бесконечно много центров. 670. Дано уравнение линии 4х2 — 4ху +у2 + 6х + 1 =0.

Определить, при каких значениях углового коэффициента k прямая

у = kx

а) пересекает эту линию в одной точке; б) касается этой линии; в) пересекает эту линию в двух точках;

г) не имеет общих точек с этой линией.

671. Составить уравнение линии второго порядка, которая, имея центр в начале координат, проходит через точку М (6; —2) и касается прямой

х —2 = 0

в точке N (2; 0).

672. Точка Р (1; —2) является центром линии второго порядка, которая проходит через точку Q (0;—3) и касается оси Ох в начале координат. Составить уравнение этой линии.

vk.com/club152685050 | vk.com/id446425943

г) х2 — 6ху + 10у2 + 10х — 32у+ 26 = 0.

680.Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет гиперболу, и найти величины её полуосей:

1)4х2 + 24ху + 11у2 + 64х + 42у + 51=0;

2)12х2 + 26ху + 12у2 — 52х — 48у + 73 = 0;

3)3х2 + 4ху — 12х + 16 = 0;

4)х2 — 6ху — 7у2 + 10х — 30у + 23 = 0.

681.Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет пару пересекающихся прямых (вырожденную гиперболу), и найти их уравнения:

а) 3х2 + 4ху + у2 — 2х — 1=0; б) х2 — 6ху + 8у2 — 4у — 4 = 0;

в) х2 — 4ху + 3у2 = 0;

г) х2 + 4ху + 3у2 — 6х — 12у + 9 = 0.

682.Не проводя преобразования координат, установить, какие геометрические образы определяются следующими уравнениями:

1)8х2—12ху+17у2+16х—12у + 3 = 0;

2)17х2 —18ху —7у2 + 34х—18у + 7 = 0;

3)2х2 + 3ху — 2у2 + 5х + 10у = 0;

4)6х2 —6ху + 9у2 —4х+18у+14 = 0;

5)5х2 —2ху + 5у2 —4х + 20у + 20 = 0.

683.Для любого эллиптического уравнения доказать, что ни один из коэффициентов А и С не может обращаться в нуль и что они суть числа одного знака.

684.Доказать, что эллиптическое уравнение второй степени ( > 0) определяет эллипс в

вырожденную гиперболу (пару пересекающихся прямых) в том и только в том случае, когда = 0.

vk.com/club152685050 | vk.com/id446425943

то дискриминант его левой части определяется формулой

(D E )2 .

695.Доказать, что параболическое уравнение

696. Доказать, что параболическое уравнение определяет параболу в том и только в том случае,

697.Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет параболу, и найти параметр этой параболы:

1)9х2 + 24ху+16у2 — 120х + 90у = 0;

2)9х2 — 24ху+16у2 — 54х—178у+181=0;

3)х2 —2ху+у2 + 6х—14у + 29 = 0;

4)9х2 — 6ху +у2 — 50х + 50у — 275 = 0.

698.Доказать, что уравнение второй степени является уравнением вырожденной линии в том и

699. Не проводя преобразования координат, установить, что каждое из следующих уравнений

определяет пару параллельных прямых, и найти их уравнения:

а) 4х2 + 4ху+у2 —12х —6у + 5 = 0; б) 4х2 — 12ху + 9у2 + 20х — 30у — 11 = 0;

в) 25х2 — 10xу +у2 + 10х — 2у —15 = 0.

700. Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет одну прямую (пару слившихся прямых), и найти уравнение этой прямой:

а) х2 —6ху + 9у2 + 4х—12у + 4 = 0; б) 9х2 + 30ху + 25у2 + 42х + 70у + 49 = 0;

в) 16х2—16ху+4у2 —72х+36у + 81=0.

vk.com/club152685050 | vk.com/id446425943

§26. Уравнения некоторых кривых, встречающихся

вматематике и её приложениях

701. Составить уравнение геометрического места точек, произведение расстояний которых до двух данных точек F1 (— с; 0) и

Черт. 23. Черт. 24.

F2 (с; 0) есть постоянная величина а2. Такое геометрическое место точек называется о в а л о м К а с с и н и (черт. 23).

702. Составить уравнение геометрического места точек, про-. изведение расстояний которых до двух данных точек F1 (— а; 0) и F2 (а; 0) есть постоянная величина а2. Такое геометрическое место точек называется л е м н и с к а т о й (черт. 24). (Уравнение лемнискаты сначала найти непосредственно, потом — рассматривая её как частный вид овала Кассини.) Составить также уравнение лемнискаты в полярных координатах, совмещая полярную ось с положительной полуосью Ох и полюс с началом координат.

703.Составить уравнение геометрического места оснований перпендикуляров, опущенных из начала координат на прямые, отсекающие от координатного угла треугольники постоянной площади S.

У к а з а н и е. Составить уравнение сначала в полярных координатах, совмещая полюс с началом координат и полярную ось с положительной полуосью Ох.

704.Доказать, что геометрическое место точек задачи 703 есть лемниската (см. задачу 702).

У к а з а н и е. Повернуть координатные оси на угол в 45°.

705.Луч а, в начальном положении совпадающий с полярной осью, вращается вокруг полюса О с постоянной угловой скоростью ω. Составить в данной системе полярных координат уравнение траектории точки М, которая, имея начальное положение в О, движется по лучу а равномерно со скоростью v (спираль Архимеда, черт. 25).

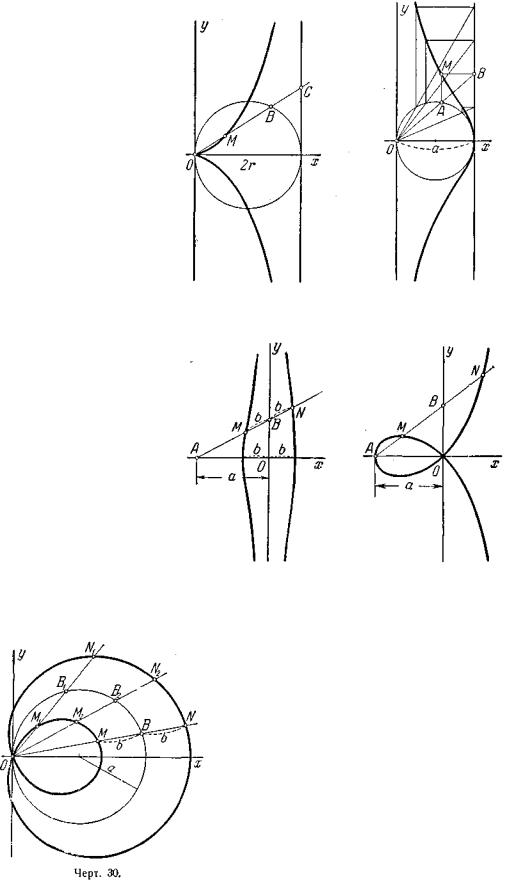
706.Дана прямая х=2r и окружность радиуса r, которая проходит через начало координат О и касается данной прямой. Из точки О проведен луч, пересекающий данную окружность в точке В и

данную прямую в точке С, на котором отложен отрезок ОМ = ВС (черт. 26). При вращении луча длина отрезка ОМ меняется и точка М

описывает кривую, называемую ц и с с о и д о й. Составить уравнение циссоиды.

707.Дана прямая х = а (а > 0) и окружность диаметра а, проходящая через начало координат О, и касающаяся данной прямой. Из точки О проведён луч, пересекающий окружность в точке А и данную прямую в точке В. Из точек А и В проведены прямые, параллельные соответственно осям Оу и Ох (черт. 27).

Точка М пересечения этих прямых при вращении луча описывает кривую, называемую в е р з ь е р о й. Составить её уравнение.

708. Из точки А (— а; 0), где a > 0, проведён луч АВ (черт. 28), на котором по обе стороны от

Черт. 25. точки В отложены отрезки ВМ и BN одинаковой длины b (b = const.). При вращении луча точки М к N описывают кривую, называемую конхоидой. Составить её уравнение сначала в полярных координатах, помещая полюс в точку А и направляя полярную ось в

vk.com/club152685050 | vk.com/id446425943

положительном направлении оси Ох, а затем перейти к данной системе декартовых прямоугольных координат.

709. Из точки А(—а; 0), где a > 0, проведён луч АВ (черт. 29), на котором по обе стороны от точки В отложены отрезки ВМ и BN, равные 0В. При вращении луча точки М и N описывают кривую, называемую с т р о ф о и д о й. Составить её уравнение сначала в полярных координатах, помещая полюс в точке А и направляя полярную ось в положительном направлении оси Ох, а затем перейти к данной системе декартовых прямоугольных координат.

710. Из начала координат проведён луч, пересекающий данную окружность x2 + y2 = 2ax (а > 0) в точке В (черт. 30); на луче

Черт. 26. Черт. 27.

по обе стороны от точки В отложены равные между собой отрезки ВМ и BN постоянной длины b, При вращении луча точки М и N

положительной полуосью Ох, а затем перейти к данной системе декартовых прямоугольных координат.

711. Отрезок длины 2а движется так, что его концы всё время находятся на координатных осях. Составить уравнение траектории основания М перпендикуляра, опущенного из начала координат на отрезок (черт. 31), сначала в полярных координатах, совмещая полюс с началом координат и полярную ось с положительной полуосью Ох, а затем перейти к данной системе декартовых прямоугольных координат. Точка М описывает кривую, называемую четырёхлепестковой розой.

vk.com/club152685050 | vk.com/id446425943

712. Отрезок длины а движется так, что его концы всё время находятся на координатных осях (черт. 32). Через концы отрезка проведены прямые, параллельные координатным осям, до их взаимного пересечения в точке Р. Составить уравнение траектории основания М перпендикуляра, опущенного из точки Р на отрезок. Эта траектория называется а с т р о и д о й.

У к а з а н и е. Составить сначала параметрические уравнения астроиды, выбирая параметр t, как указано на черт. 32 (затем исключить параметр t).

713. Из точки В пересечения луча ОВ с окружностью х2+у2 = ах опущен перпендикуляр ВС на ось Ох. Из точки С на луч ОВ опущен перпендикуляр СМ. Вывести уравнение траектории точки М сначала в полярных координатах, совмещая полюс с началом координат и полярную ось с положительной полуосью Ох, а затем перейти к данной системе декартовых прямоугольных координат.

714. Нить, намотанная на окружность х2 + у2 = а2, разматывается так, что в точке В, где нить отделяется от окружности, она остаётся касательной к ней (черт. 33). Найти параметрические уравнения линии, описываемой

концом нити, если начальным положением конца является точка А (а; 0), где a > 0. Линия, о которой идёт речь, называется э в о л ь в е н т о й к р у г а.

715.Круг радиуса а катится без скольжения по оси Ох. Траектория некоторой точки М окружности этого круга называется циклоидой (черт. 34). Вывести параметрические уравнения циклоиды, принимая в качестве

параметра t угол, на который поворачивается катящаяся окружность вокруг своего центра; считать при этом, что в начальный момент (t = 0) точка М находится в начале координат. Исключить параметр t из полученных уравнений.

716.Круг радиуса а катится без скольжения по окружности х2

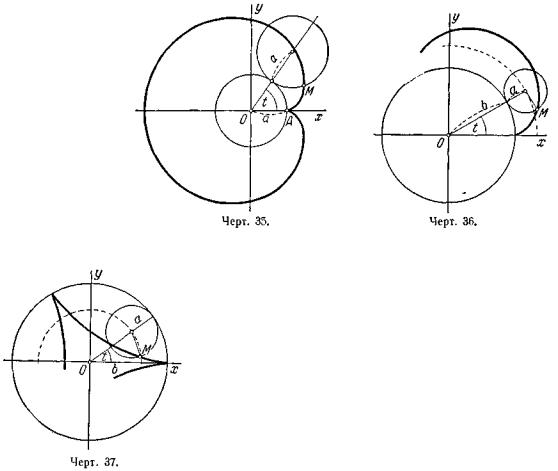
катящегося круга называется к а р д и о и д о й (черт. 35). Вывести параметрические уравнения кардиоиды, выбирая в качестве параметра t угол наклона к оси Ох радиуса неподвижной окружности, проведённого в точку касания с подвижной. Считать при этом, что в начальный момент (t = Q) точка М находится справа на оси Ох. Перейти к полярным координатам при условии, что направление полярной оси совпадает с положительным направлением оси абсцисс, а

vk.com/club152685050 | vk.com/id446425943

(черт. 36). Вывести параметрические уравнения эпициклоиды, выбирая в качестве параметра t угол наклона к оси Ох радиуса неподвижной окружности, проведённого в точку касания с подвижной; считать при этом, что в начальный момент (t = 0) точка М находится справа на оси Ох. Доказать, что кардиоида (см. задачу 716) есть частный вид эпициклоиды.

718. Круг радиуса а катится без скольжения по окружности х2 + у2 = b2, оставаясь внутри неё. Траектория некоторой точки М окружности катящегося круга называется гипоциклоидой (черт. 37). Вывести параметрические уравнения гипоциклоиды, выбирая в качестве параметра t угол наклона к оси Ох радиуса неподвижной окружности, проведённого в точку касания с подвижной; считать при этом, что в начальный момент (t = 0) точка М находится справа на оси Ох,

Доказать, что астроида (см. задачу 712) есть частный вид гипоциклоиды.