Линейная Агебра

vk.com/club152685050 | vk.com/id446425943

точки F ( 2p ;0) равно расстоянию до данной прямой х = — 2p Это геометрическое место

называется параболой, точка F — фокусом параболы, данная прямая — её директрисой. 193. Вывести уравнение геометрического места точек, для которых отношение расстояния

194. Вывести уравнение геометрического места точек, для которых отношение расстояния

195. Вывести уравнение геометрического места точек, для которых кратчайшие расстояния до двух данных окружностей (x+3)2+ y2=1,

(x-3)2+ y2=81 равны между собой.

196. Вывести уравнение геометрического места точек, для которых кратчайшие расстояния до двух данных окружностей (х-10)2 +y2=289, (x-10)2+ y2=1, равны между собой.

197.Вывести уравнение геометрического места точек, для которых кратчайшие расстояния до данной окружности (х — 5)2+ y2=9, и до данной прямой x+2 = 0 равны между собой.

198.Прямая перпендикулярна полярной оси и отсекает на ней отрезок, равный 3. Составить уравнение этой прямой в полярных координатах.

уравнение этого луча в полярных координатах.

200. Прямая проходит через полюс и наклонена к полярной оси под углом 45°. Составить уравнение этой прямой в полярных координатах.

201. В полярных координатах составить уравнение геометрического места точек, расстояния которых от полярной оси равны 5.

202. Окружность радиуса R = 5 проходит через полюс, её центр лежит на полярной оси. Составить уравнение этой окружности в полярной системе координат.

203. Окружность радиуса R = 3 касается полярной оси в полюсе. Составить уравнение этой окружности в полярной системе координат,

vk.com/club152685050 | vk.com/id446425943

§ 11. Параметрические уравнения линии

Обозначим буквами х и у координаты некоторой точки М; рассмотрим две функции аргумента t:

x (t),

y (t)).

При изменении t величины х и у будут, вообще говоря, меняться, следовательно, точка М будет перемещаться. Равенства (1) называются параметрическими уравнениями линии, которая является траекторией точки М; аргумент t носит название параметра. Если из равенства (1) можно исключить параметр t, то получим уравнение траектории точки М в виде

F(x, y) = 0.

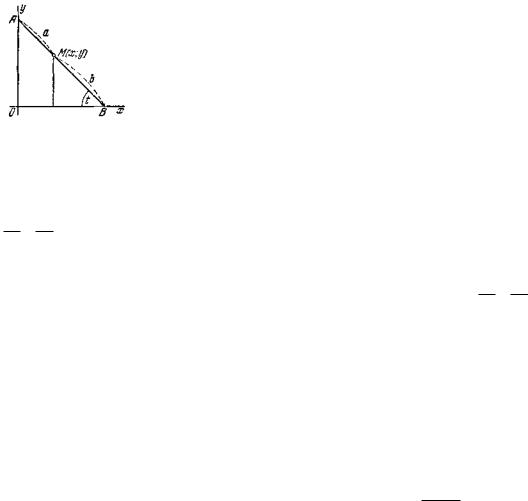
204. Стержень АВ скользит своими концами А к В по координатным осям. Точка М делит стержень на две части АМ = а и ВМ = b. Вывести параметрические уравнения траектории точки М, приняв в качестве

параметра

Черт. 8. угол t = <OBA (черт. 8). Исключить затем параметр t и найти уравнение траектории точки М в виде F(x, y) = 0

205. Траекторией точки М является эллипс, уравнение которого

принимая в качестве параметра t угол наклона отрезка ОМ к оси Ох.

принимая в качестве параметра t угол наклона отрезка ОМ к оси Ох.

207. Траекторией точки М является парабола, уравнение которой у2 =2рх (см. задачу 192). Вывести параметрические уравнения траектории точки М, принимая в качестве параметра t:

1)ординату точки М;

2)угол наклона отрезка ОМ к оси Ох;

3)угол наклона отрезка FM к оси Ох, где точка F — фокус параболы. 208. Даны полярные уравнения следующих линий:

Составить параметрические уравнения этих линий в декартовых прямоугольных координатах, совмещая положительную полуось абсцисс с полярной осью и выбирая в качестве параметра полярный угол.

209. Даны параметрические уравнения линий:

vk.com/club152685050 | vk.com/id446425943

§12. Общее уравнение прямой. Уравнение прямой

сугловым коэффициентом. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых

Вдекартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую. Уравнение вида

Ах + Ву + С = 0 (1)

называется общим уравнением прямой.

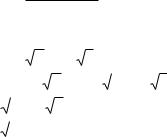
Угол а, определяемый, как показано на черт. 9, называется углом наклона прямой к оси Ох. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой k:

k = tg α,

Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом; k — угловой коэффициент, b — величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.

Если прямая задана общим уравнением Ах+Ву+С=0, то её угловой коэффициент

Черт. 9

Уравнение у — y0 = k(x—ха) является уравнением прямой, которая проходит через точку М0 (х0 ; у0) и имеет угловой коэффициент k.

Если прямая проходит через точки M1 (x1; у1,) и М2 (х2; у2), то её угловой коэффициент определяется по формуле

Является уравнением прямой, проходящей через две точки М1 (x1; y 1) и M 2(x2 ; у2)

Если известны угловые коэффициенты двух прямых k1 и k2, то один из углов φ между этими прямыми определяется по формуле

Признаком параллельности двух прямых является равенство их угловых коэффициентов k1 =k2

Признаком перпендикулярности двух прямых является соотношение

Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку.

*) Здесь и везде в дальнейшем под уравнением сторон мы будем понимать уравнения прямых, на которых лежат стороны.

210.Определить, какие из точек М1(3; 1), М2(2; 3), М3(6; 3), М4(— 3; —3). М5(3; —1), М6(—

2; 1) лежат на прямой 2x —3у —3 = 0 и какие не лежат на ней.

211.Точки Р1, Р2, Р3, P4, и P5 расположены на прямой 3x— 2у —— 6 = 0; их абсциссы

соответственно равны числам: 4, 0, 2, — 2 и — 6. Определить ординаты этих точек.

vk.com/club152685050 | vk.com/id446425943

212.Точки Q 1; Q 2, Q3, Q 4 и Q 5 расположены на прямой х—3у + 2 = 0; их ординаты соответственно равны числам: 1, 0, 2, — 1, 3. Определить абсциссы этих точек.

213.Определить точки пересечения прямой 2х — 3у—12 = 0 с координатными осями и построить эту прямую на чертеже.

214.Найти точку пересечения двух прямых

221. Определить угловой коэффициент k и отрезок b, отсекаемый на оси Оу, для каждой из прямых:

222.Дана прямая 5х+3у — 3 = 0. Определить угловой коэффициент k прямой: 1) параллельной данной прямой; 2) перпендикулярной к данной прямой.

223.Дана прямая 2х+3у+4 = 0. Составить уравнение прямой, проходящей через точку M0(2;

1):

1) параллельно данной прямой;

2) перпендикулярно к данной прямой.

224.Даны уравнения двух сторон прямоугольника

иодна из его вершин A(2; —3). Составить уравнения двух других сторон этого прямоугольника.

225. Даны уравнения двух сторон прямоугольника

х— 2у = 0, х — 2y+15 = 0

иуравнение одной из его диагоналей

7x+y—15 = 0.

Найти вершины прямоугольника.

226. Найти проекцию точки Р(—6; 4) на прямую

4x— 5у+3 = 0.

vk.com/club152685050 | vk.com/id446425943

230.Составить уравнения прямых, проходящих через вершины треугольника A (5; —4), В(—1; 3), С(—3; —2) параллельно противоположным сторонам.

231.Даны середины сторон треугольника: М1(2; 1), М2(5; 3) и М3(3; —4). Составить уравнения его сторон.

232.Даны две точки: Р(2; 3) и Q(—1; 0). Составить уравнение прямой, проходящей через точку Q перпендикулярно к отрезку PQ.

233.Составить уравнение прямой, если точка Р(2; 3) служит основанием перпендикуляра, опущенного из начала координат на эту прямую.

234.Даны вершины треугольника М1(2; 1), M2(—1; —1) и M 3(3; 2). Составить уравнения его высот.

235.Стороны треугольника даны уравнениями 4х—у — 7 = 0, х+3у — 31 = 0, х+5у — 7 = 0. Определить точку пересечения его высот.

236.Даны вершины треугольника A(1; —1), В(—2; 1) и С(3; 5). Составить уравнение перпендикуляра, опущенного из вершины A на медиану, проведённую из вершины В.

237.Даны вершины треугольника А (2; —2), В(3; —5) и С(5; 7). Составить уравнение перпендикуляра, опущенного из вершины С на биссектрису внутреннего угла при вершине

A .

238.Составить уравнения сторон и медиан треугольника с вершинами A(3; 2), В(5; —2),

С(1; 0).

239.Через точки М1(—1; 2) и М2(2; 3) проведена прямая. Определить точки пересечения этой прямой с осями координат.

240.Доказать, что условие, при котором три точки M1(x1, y1,), М2(x2, y2,), и М3(х3; у3) лежат на одной прямой, может быть записано в следующем виде:

241. Доказать, что уравнение прямой, проходящей через две данные точки М1 (х1; у2) и M2(х2;_у2), может быть записано в следующем виде:

x y 1

x1 y1 1 0 . x2 y2 1

242.Даны последовательные вершины выпуклого четырёхугольника A(— 3; —1), B(3; 9), С(7; 6) и D(— 2; — 6). Определить точку пересечения его диагоналей.

243.Даны две смежные вершины А(— 3; — 1) и B(2; 2) параллелограмма АВСD и точка Q(3; 0) пересечения его диагоналей. Составить уравнения сторон этого параллелограмма.

244.Даны уравнения двух сторон прямоугольника

5х+1у — 7 = 0, 5х + 2у — 36 = 0

vk.com/club152685050 | vk.com/id446425943

§ 13. Неполные уравнения прямой. Совместное исследование уравнений двух и трёх прямых. Уравнение прямой «в отрезках»

Если в общем уравнении прямой

Ах + Ву + С = 0 (1)

один или два из трёх коэффициентов (считая и свободный член) обращаются в нуль, то уравнение называется неполным. Возможны следующие случаи:

1)С = 0; уравнение имеет вид Ах +By = 0 и определяет прямую, проходящую через начало координат.

2)B = 0 (A≠0); уравнение имеет вид Ах + С = 0 и определяет прямую,

3)B = 0, С = 0 (A≠0); уравнение может быть записано в виде х = 0 и определяет ось ординат.

4)А=0 (B≠0); уравнение имеет вид By + С = 0 и определяет прямую, перпендикулярную к

который отсекает прямая на оси Оу, считая от начала координат.

5) А = 0, С = 0 (B≠0); уравнение может быть записано в виде у = 0 и определяет ось абсцисс. Если ни один из коэффициентов уравнения (1) не равен нулю, то его можно преобразовать к

на координатных осях.

Уравнение (2) называется уравнением прямой «в отрезках». Если две прямые даны уравнениями

A1 + B1 y + C1 = 0,

то могут представиться три случая:

определяют одну и ту же прямую. 285. Определить, при каком значении а прямая

(а + 2)x + (а2 – 9)y + 3а2 – 8а + 5 = О

1)параллельна оси абсцисс;

2)параллельна оси ординат;

3)проходит через начало координат.

Вкаждом случае написать уравнение прямой.

286.Определить, при каких значениях т и п прямая

(т + 2п – 3) х + (2т – n + 1)y +6m + 9 = 0

параллельна оси абсцисс и отсекает на оси ординат отрезок, равный – 3 (считая от начала координат). Написать уравнение этой прямой.

287. Определить, при каких значениях тип прямая

(2т – п + 5) х + (т + 3n – 2) у + 2m + 7n + 19 = 0