
- •Обработка результатов измерений. Введение
- •Теория погрешностей
- •Классификация измерений
- •Классификация погрешностей
- •Оценка истинного значения измеряемой величины по результатам эксперимента. Понятие случайной величины и вероятностного распределения
- •Распределение Гаусса и его основные характеристики
- •Понятие доверительного интервала и доверительной вероятности (надежности)
- •Распределение Стьюдента
- •Выявление промахов
- •Выбор числа необходимых измерений и учет погрешности измерительного прибора
- •Порядок обработки результатов прямых измерений
- •Расчет погрешностей косвенных измерений
- •Порядок обработки результатов при косвенных измерениях
- •Практические рекомендации
- •2.1. Подготовка таблиц в лабораторном журнале и проведение лабораторных измерений
- •2.2. Определение приборных погрешностей
- •2.3. Методика расчета погрешностей прямых измерений
- •2.4. О приближенных вычислениях
- •2.5. Правила приближенных вычислений
- •2.6. Правила построения графиков
- •Приставки для образования наименований кратных и дольных единиц
- •Выражение физических величин в одной системе единиц
- •Литература
Распределение Стьюдента
Формула
(3), по которой оценивается среднеквадратичное
отклонение ,
является справедливой лишь при
![]() .
Число измерений в реальных опытах не
может быть бесконечно большим, поэтому
использовать среднеквадратичное
отклонение для ограниченного числа
измерений нельзя.
.
Число измерений в реальных опытах не
может быть бесконечно большим, поэтому
использовать среднеквадратичное
отклонение для ограниченного числа
измерений нельзя.
Чтобы
получить оценку доверительного интервала
для величины а
в случае малых n,
в теории погрешностей вместо отношения
![]() ,
вводят величину
,
вводят величину
![]() (5)
(5)
Эта величина (коэффициент Стьюдента) является функцией числа измерений n и величины - доверительной вероятности, которая нам задается или же мы ее выбираем сами.
Оказывается, что случайная величина при малых n распределена не по нормальному закону (1), а по закону, открытому Стьюдентом.
Вид этого закона существенно зависит от выбора n.
Плотность вероятности распределения P(t), соответствующая закону Стьюдента, имеет вид:
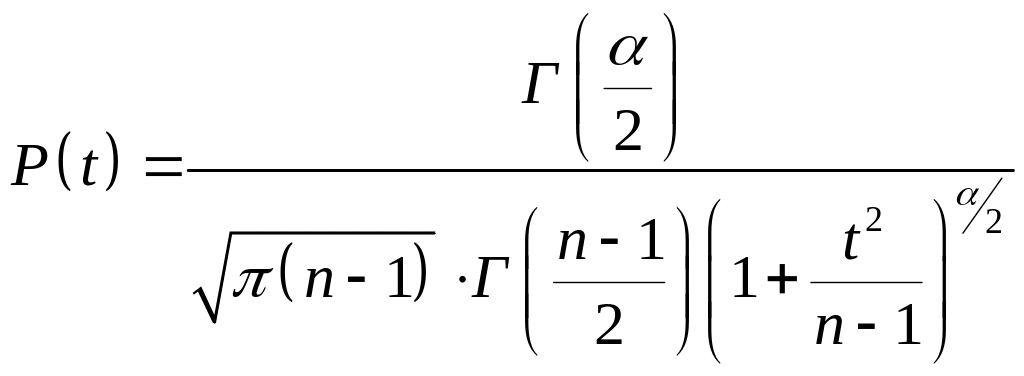 , (6)
, (6)
где
![]() — гамма-функции.
— гамма-функции.
Н а
рис.6 приведены кривые распределения
Стьюдента для различных значений n.
а
рис.6 приведены кривые распределения
Стьюдента для различных значений n.
При
![]() распределение Стьюдента переходит в
распределение Гаусса. Распределение
Стьюдента позволяет оценить величину
погрешности результата X
при заданной доверительной вероятности
,
или, наоборот, при заданном X
найти величину .
Действительно, если выбрать на оси
t(n,)
некоторое значение t
(рис.6), то вероятность
определяется заштрихованной площадью,
причем величина
будет зависеть не только от t,
но и от n.
Значение коэффициента Стьюдента t
для различных значений n
и ,
рассчитанные в соответствии с законом
Стьюдента, приведены в таблице 2.
распределение Стьюдента переходит в
распределение Гаусса. Распределение
Стьюдента позволяет оценить величину
погрешности результата X
при заданной доверительной вероятности
,
или, наоборот, при заданном X
найти величину .
Действительно, если выбрать на оси
t(n,)
некоторое значение t
(рис.6), то вероятность
определяется заштрихованной площадью,
причем величина
будет зависеть не только от t,
но и от n.
Значение коэффициента Стьюдента t
для различных значений n
и ,
рассчитанные в соответствии с законом
Стьюдента, приведены в таблице 2.
Задавая
надежность ,
равную определенной величине, при данном
значении n,
по табл.2 можно определить коэффициент
t.
Тогда, определив предварительно
![]() по формуле (3), можно оценить абсолютную
погрешность результата (доверительный
интервал)
Х
по формуле:
по формуле (3), можно оценить абсолютную
погрешность результата (доверительный
интервал)
Х
по формуле:
![]() (7)
(7)
Таблица 2.
|
|
||||||
n |
0,2 |
0,4 |
0,6 |
0,8 |
0,9 |
0,95 |
0,99 |
2 |
0,33 |
0,73 |
1,38 |
3,1 |
6,31 |
12,7 |
63,7 |
3 |
0,29 |
0,62 |
1,06 |
1,9 |
2,92 |
4,30 |
9,52 |
4 |
0,28 |
0,58 |
0,98 |
1,6 |
2,35 |
3,18 |
5,84 |
5 |
0,27 |
0,57 |
0,94 |
1,5 |
2,13 |
2,78 |
4,60 |
6 |
0,27 |
0,56 |
0,92 |
1,5 |
2,02 |
2,57 |
4,03 |
7 |
0,27 |
0,55 |
0,90 |
1,4 |
1,94 |
2,45 |
3,17 |
8 |
0,26 |
0,55 |
0,90 |
1,4 |
1,89 |
2,36 |
3,50 |
9 |
0,26 |
0,54 |
0,90 |
1,4 |
1,86 |
2,31 |
3,36 |
10 |
0,26 |
0,54 |
0,86 |
1,4 |
1,83 |
2,26 |
3,25 |
15 |
0,26 |
0,54 |
0,87 |
1,3 |
1,76 |
2,14 |
2,98 |
20 |
0,26 |
0,53 |
0,85 |
1,3 |
1,73 |
2,09 |
2,86 |
30 |
0,26 |
0,53 |
0,85 |
1,3 |
1,70 |
2,05 |
2,76 |
40 |
0,26 |
0,53 |
0,85 |
1,3 |
1,69 |
2,02 |
2,71 |
60 |
0,25 |
0,53 |
0,85 |
1,3 |
1,67 |
2,00 |
2,66 |
∞ |
0,25 |
0,52 |
0,84 |
1,3 |
1,65 |
1,95 |
2,59 |
Истинное
значение измеряемой величины а
будет находиться в пределах интервала
(![]() )
с вероятностью ,
т. е.
)
с вероятностью ,
т. е.
![]() (8)
(8)
Объективным критерием качества проведенных измерений является относительная погрешность, определяемая отношением абсолютной погрешности к среднему значению измеряемой величины:
![]() (9)
(9)
