Формула симпсона
Формула для вычисления объёмов тел с двумя параллельными основаниями:
,
где
Qн – площадь
нижнего основания, Qв
– площадь верхнего основания, Qс
– площадь среднего сечения тела. Под
средним сечением тела здесь понимается
фигура, полученная от пересечения тела
плоскостью, параллельной плоскостям
оснований и находящейся на равном
расстоянии от этих плоскостей. Через h
обозначена высота тела.
Из Ф.С., как частный случай, получаются многие известные формулы объёмов тел, изучаемых в школе (усечённой пирамиды, цилиндра, шара и др.).
Теорема синусов
Теорема плоской тригонометрии, устанавливающая зависимость между сторонами a, b, c произвольного треугольника и синусами противолежащих этим сторонам углов:
,
где
R – радиус описанной
около треугольника окружности.
Для сферической тригонометрии Т.С. аналитически выражается так:
.
Теорема стюарта
Заключается в следующем: если A, B, C – три вершины треугольника, а D – любая точка на стороне BC, то имеет место соотношение:
AD2*BC = AB2*CD + AC2*BD – BC*BD*CD , Т.С. названа по имени доказавшего её английского математика М. Стюарта и опубликовавшего её в труде «Некоторые общие теоремы» (1746, Эдинбург). Теорему сообщил Стюарту его учитель Р. Симсон, который опубликовал эту теорему лишь в 1749 г. Т.С. применяется для нахождения медиан и биссектрисс треугольников.
Теорема тангенсов (формула региомонтана)
Формула плоской тригонометрии, устанавливающая зависимость между длинами двух сторон треугольника и тангенсами полусуммы и полуразности противолежащих им углов. Т.Т. имеет вид:
,
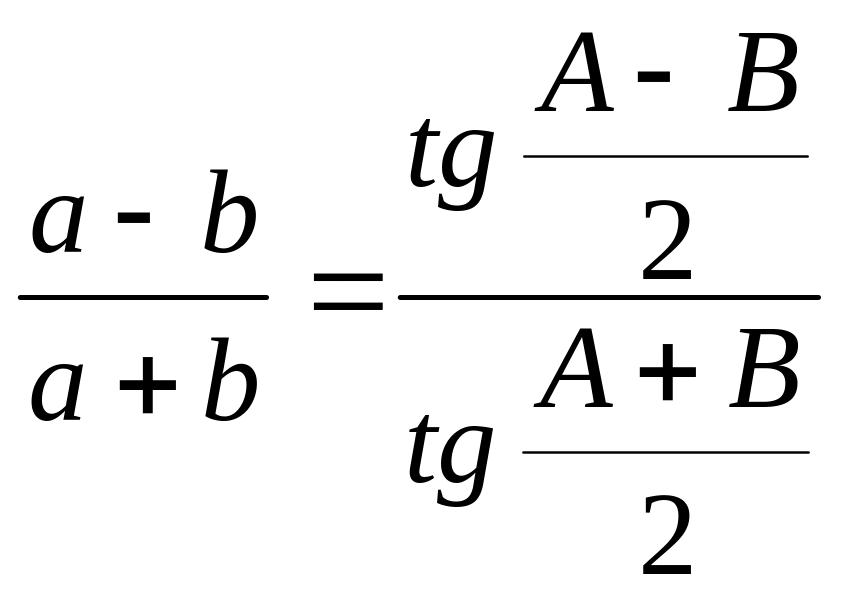где
a, b
– стороны треугольника, A,
B – соответственно
противолежащие этим сторонам углы.
Т.Т. также называют формулой Региомонтана по имени немецкого астронома и математика Иоганна Мюллера (по-латински Regiomontanus), установившего эту формулу. И. Мюллера называли «Кёнигсбержец»: по-немецки König – король, Berg – гора, а по-латински «король» и «гора» в родительном падеже – regis и montis. Отсюда «Региомонтан» - латинизированная фамилия И. Мюллера.
«Толковый словарь математических терминов», О.В. Мантуров
ФОРМУЛЫ И ТЕОРЕМЫ НА VADIMSOFT-BEST.NAROD.RU