Основная теорема алгебры

Теорема, заключающаяся в том, что всякий многочлен степени n (n>0):

f(z) = a₀zⁿ + a₁z^n-1 + … + a_n , где a₀ / 0, над полем комплексных чисел имеет по крайней мере один корень z₁, так что f(z₁)=0. Из О.Т.А. и из теоремы Безу вытекает, что многочлен f(z) имеет в поле комплексных чисел ровно n корней (с учётом их кратностей). Действительно, согласно теореме Безу f(z) делится на z – z₁ (без остатка), т.е. f(z) = f₁(z)(z – z₁), а отсюда многочлен f₁(z) (n – 1)-й степени по О.Т.А. также имеет корень z₂ и т.д. В конечном счёте мы придём к заключению, что f(z) имеет ровно n корней:

f(z) = a₀(z – z₁)(z – z₂) ... (z – z_n).

О.Т.А. называется так потому, что основное содержание алгебры в XVII-XVIII вв. сводилось к решению уравнений. О.Т.А. была доказана впервые в XVII в. французским математиком Жираром, строгое же доказательство было дано в 1799 г. немецким математиком Гауссом.

Теорема безу

Теорема об остатке от деления произвольного многочлена на линейный двучлен. Она формулируется следующим образом: остаток от деления произвольного многочлена f(x) на двучлен x – a равен f(a). Т.Б. названа по имени впервые сформулировавшего и доказавшего её французского математика XVIII в. Безу.

Из Т.Б. вытекают следующие следствия: 1) если многочлен f(x) делится (без остатка) на x – a, то число a является корнем f(x); 2) если число a является корнем многочлена f(x), то f(x) делится (без остатка) на двучлен x – a; 3) если многочлен f(x) имеет по крайней мере один корень, то этот многочлен имеет ровно столько корней, какова степень этого многочлена (при этом учитывается кратность корней).

Теорема чевы

Если прямые, соединяющие вершины треугольника АВС с точкой О, лежащей в плоскости треугольника, пересекают противоположные стороны (или их продолжения) соответственно в точках A’ B’ C’, то справедливо равенство:

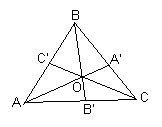(*) При этом отношение отрезков рассматривается как положительное, если эти отрезки имеют одинаковое направление, и отрицательное – в противном случае.

Т.Ч. можно записать и в такой форме: (ABC’)*(BCA’)*(CAB’) = 1, где (АВС’) – простое отношение трёх точек A, B и C’. Справедлива и обратная теорема: если точки C’, A’, B’ расположены соответственно на сторонах AB, BC и СА треугольника или их продолжениях так, что выполняется равенство (*), то прямые АА’, BB’ и CC’, пересекаются в одной точке или параллельны (пересекаются в несобственной точке).

Прямые AA’, BB’ и СС’, пересекающиеся в одной точке и проходящие через вершины треугольника, называются прямыми Чевы или чевианами. Т.Ч. носит проективный характер. Т.Ч. метрически двойственна теореме Менелая. Т.Ч. названа по имени итальянского геометра Джованни Чева, доказавшего её (1678).

Теорема косинусов

1. Т.К. плоской тригонометрии – утверждение о том, что во всяком треугольнике квадрат любой его стороны равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними:

c² = a² + b² – 2abcosC , где a, b, c – длины сторон треугольника, а C – угол, заключённый между сторонами a и b. Т.К. часто используется при решении задач элементарной геометрии и тригонометрии

2. Т.К. для стороны сферического треугольника: косинус одной стороны сферического треугольника равняется произведению косинусов двух других его сторон плюс произведение синусов тех же сторон на косинус угла между ними:

cosa = cosb*cosc + sinb*sinc*cosA

3. Т.К. для угла сферического треугольника: косинус угла сферического треугольника равен произведению косинусов двух других углов, взятому с противоположным знаком, плюс произведение синусов двух других углов на косинус стороны, противолежащей первому углу:

cosA =-cosBcosC + sinBsinCcosa.