
- •Основная теорема алгебры
- •Теорема безу
- •Теорема чевы
- •Теорема косинусов
- •Теорема эйлера
- •Теорема фалеса
- •Великая теорема ферма
- •Малая теорема ферма
- •Неравенство гёльдера
- •Формула кардано
- •Неравенство коши
- •Теорема менелая
- •Неравенство минковского
- •Формулы мольвейде
- •Бином ньютона
- •Полиномиальная теорема
- •Теорема польке
- •Теорема птолемея
- •Формула симпсона
- •Теорема синусов
- •Теорема стюарта
- •Теорема тангенсов (формула региомонтана)
Неравенство минковского
Неравенство для p-х степеней чисел, имеющее вид:
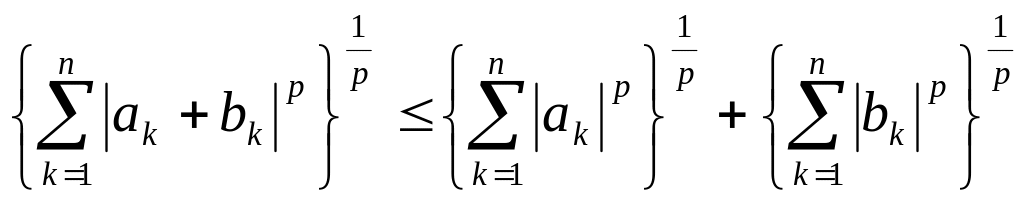 ,
где
целое p>1,
а ak
и bk
– неотрицательные числа. Н.М. является
обобщением известного «неравенства
треугольника», утверждающего, что длина
одной стороны треугольника не больше
суммы длин двух других его сторон; для
n-мерного
пространства расстояние между точками
x=(x1,
x2,
…, xn)
и y=(y1,
y2,
…, yn)
определяется числом
,
где
целое p>1,
а ak
и bk
– неотрицательные числа. Н.М. является
обобщением известного «неравенства
треугольника», утверждающего, что длина
одной стороны треугольника не больше
суммы длин двух других его сторон; для
n-мерного
пространства расстояние между точками
x=(x1,
x2,
…, xn)
и y=(y1,
y2,
…, yn)
определяется числом
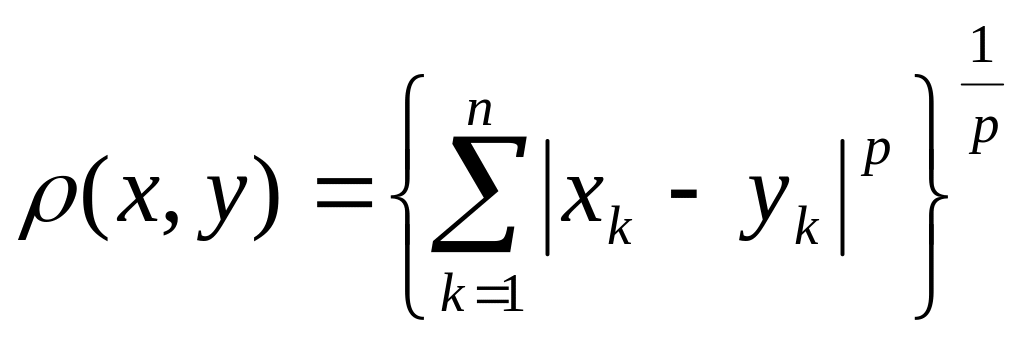 Н.М.
было установлено немецким математиком
Г. Минковским в 1896 г.
Н.М.
было установлено немецким математиком
Г. Минковским в 1896 г.
Формулы мольвейде
Формулы плоской тригонометрии, выражающие следующую зависимость между сторонами (их длинами) и углами треугольника:
 ;
;
 ,
где
a,
b,
c
– стороны, а A,
B,
C
– углы треугольника. Ф.М. названы по
имени немецкого математика К. Мольвейде,
использовавшего их, хотя эти формулы
были известны и другим математикам.
,
где
a,
b,
c
– стороны, а A,
B,
C
– углы треугольника. Ф.М. названы по
имени немецкого математика К. Мольвейде,
использовавшего их, хотя эти формулы
были известны и другим математикам.
Бином ньютона
Название формулы, выражающей целую неотрицательную степень двучлена a+b в виде суммы степеней его слагаемых. Б.Н. имеет вид:
![]() ,
где
Cnk
– биноминальные коэффициенты, равные
числу сочетаний из n
элементов по k,
т.е.
,
где
Cnk
– биноминальные коэффициенты, равные
числу сочетаний из n
элементов по k,
т.е.
![]() или
или
![]() .
.
Если биноминальные коэффициенты для различных n=0, 1, 2, …, записать в последовательно идущие строки, то придём к треугольнику Паскаля.
В случае произвольного действительного числа (а не только целого неотрицательного) Б.Н. обобщается в биноминальный ряд, а в случае увеличения числа слагаемых с двух на большее число – в полиномиальную теорему.
Полиномиальная теорема
Обобщение формулы бинома Ньютона на случай возведения в целую неотрицательную степень n суммы k слагаемых (k>2):
 ,
где
суммирование в правой части распространено
на всевозможные наборы целых
неотрицательных чисел a1,
a2,
…, ak,
дающих в сумме n.
Коэффициенты A(n)a1,
a2,
… ,ak
носят
название полиномиальных и выражаются
следующим образом:
,
где
суммирование в правой части распространено
на всевозможные наборы целых
неотрицательных чисел a1,
a2,
…, ak,
дающих в сумме n.
Коэффициенты A(n)a1,
a2,
… ,ak
носят
название полиномиальных и выражаются
следующим образом:
 При
k=2
полиномиальные коэффициенты становятся
биноминальными коэффициентами.
При
k=2
полиномиальные коэффициенты становятся
биноминальными коэффициентами.
Теорема польке
Формулируется так: три отрезка произвольной длины, лежащие в одной плоскости и исходящие из общей точки под произвольными углами друг к другу, могут быть приняты за параллельную проекцию пространственного ортогонального репера i, j, k (|i| = |j| =|k|).
Теорема была сформулирована немецким геометром К. Польке (1860) без доказательства, а затем была обобщена немецким математиком Г. Шварцем, который дал её элементарное доказательство. Теорему Польке-Шварца можно формулировать так: любой невырожденный четырёхугольник с его диагоналями можно рассматривать как параллельную проекцию тетраэдра, подобного любому данному. Т.П. имеет большое практическое значение (любой четырёхугольник с его диагоналями можно принять, например, за изображение правильного тетраэдра) и является одной из основных теорем аксонометрии.
Теорема птолемея
Теорема элементарной геометрии, устанавливающая зависимость между сторонами и диагоналями четырёхугольника, вписанного в окружность: во всяком выпуклом четырёхугольнике, вписанном в окружность, произведение диагоналей равно сумме произведений его противоположных сторон, т.е. имеет место равенство:
AC*BD = AB*CD
+ BC*AD
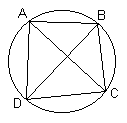
Т.П. названа по имени древнегреческого учёного Клавдия Птолемея, доказавшего эту теорему. Т.П. используется при решении задач по элементарной геометрии, при доказательстве частного случая теоремы сложения синусов.
