3.2 Завдання 2 Планування дф та пф експерименту

3.2.1 Загальні вказівки

Якщо наперед не відомий аналітичний вираз функції відгуку, то можна розглядати не саму функцію, а її розкладання, наприклад в статечній ряд у вигляді полінома

Y=В₀ + B₁Х₁ + … + B_nХ_n + В₁₂Х₁Х₂ + … В_nn-1Х_nХ_n-1 + В₁₁Х₁² + … + В_nnX_n² +….

Розкладання в статечній ряд функції можливо в тому випадку, якщо сама функція є безперервною і гладкою. На практиці зазвичай обмежуються числом членів статечного ряду і апроксимують функцію поліномом деякої міри.

Зв'язок між кодовим і натуральним виразом чинника задається формулою

, (2.1)

де - натуральне значення чинника;

- значення -го чинника на нульовому рівні;

- інтервал варіювання -го чинника.

Перевірка відтворюваності дослідів. При однаковому числі паралельних дослідів на кожному поєднанні рівнів чинників відтворюваність процесу, перевіряється по критерію Кохрена:

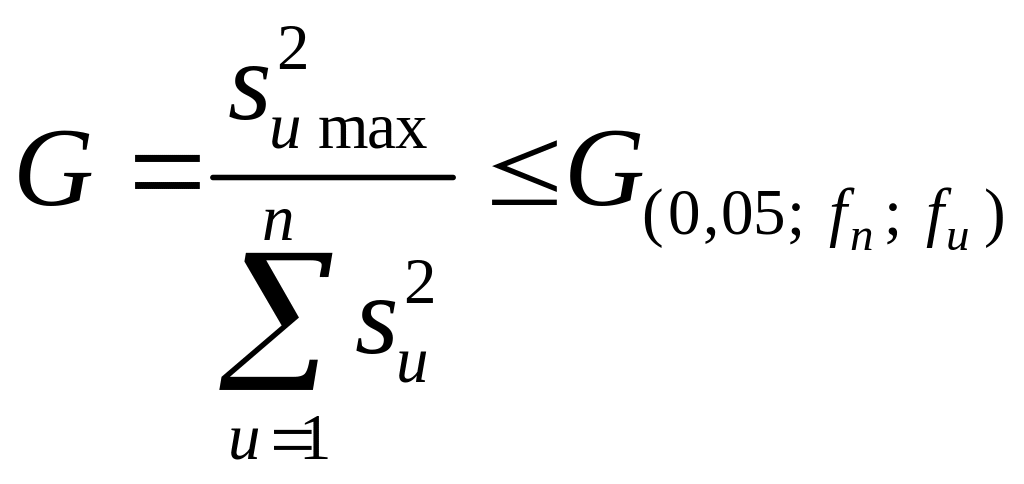, (2.2)

де дисперсія, що характеризує розсіяння результатів дослідів на -м поєднанні рівнів чинників:

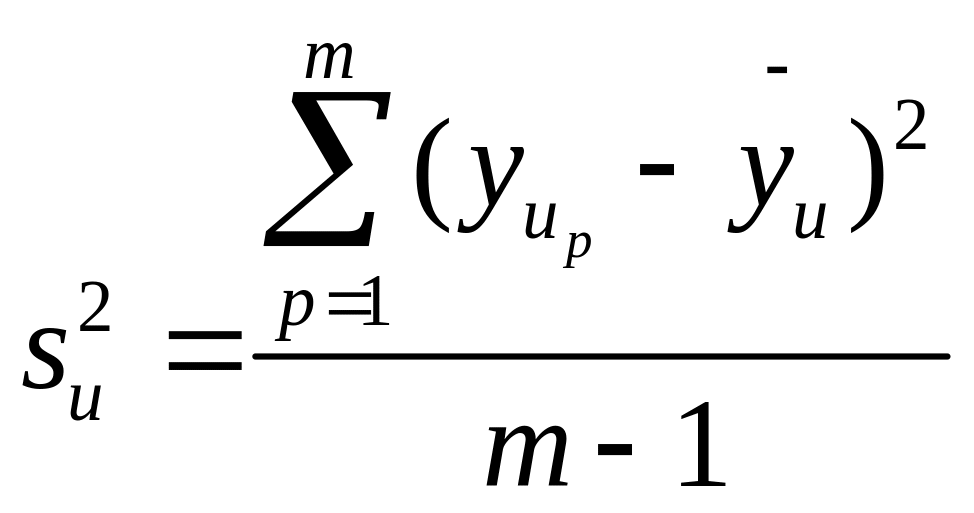
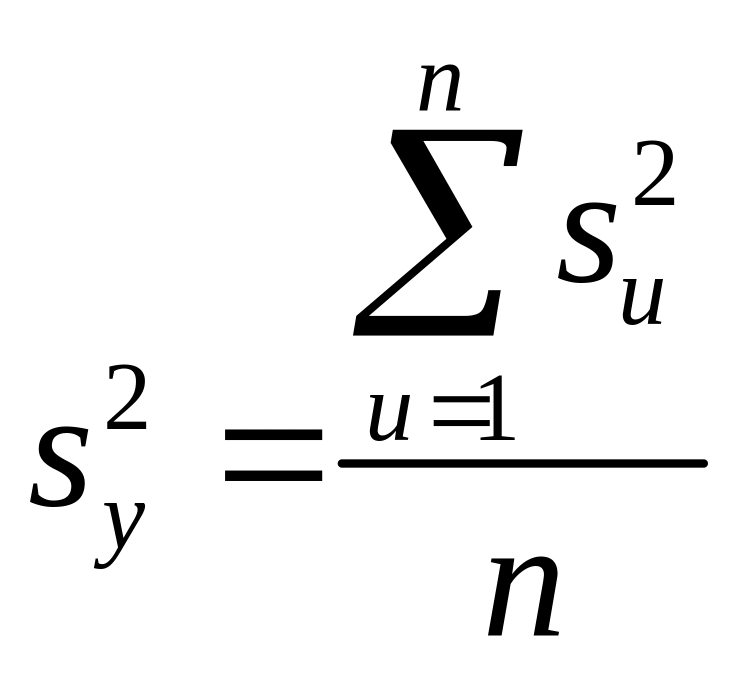. (2.3)

де - число паралельних дослідів;

- найбільша з дисперсій в строчках плану;

- табличне значення критерію Кохрена при 5%-ном рівні значущості;

- число незалежних оцінок дисперсії;

- число мір свободи кожної оцінки.

Процес вважається відтворним, якщо виконується нерівність (2.2). При цьому дисперсія відтворюваності (помилка досвіду) визначається по формулі

. (2.4)

Якщо нерівність (2.2) не виконується, то необхідно прийняти заходи до уточнення вимірювань в досвіді з максимальною дисперсією.

У разі відтворного процесу розраховують коефіцієнти регресії

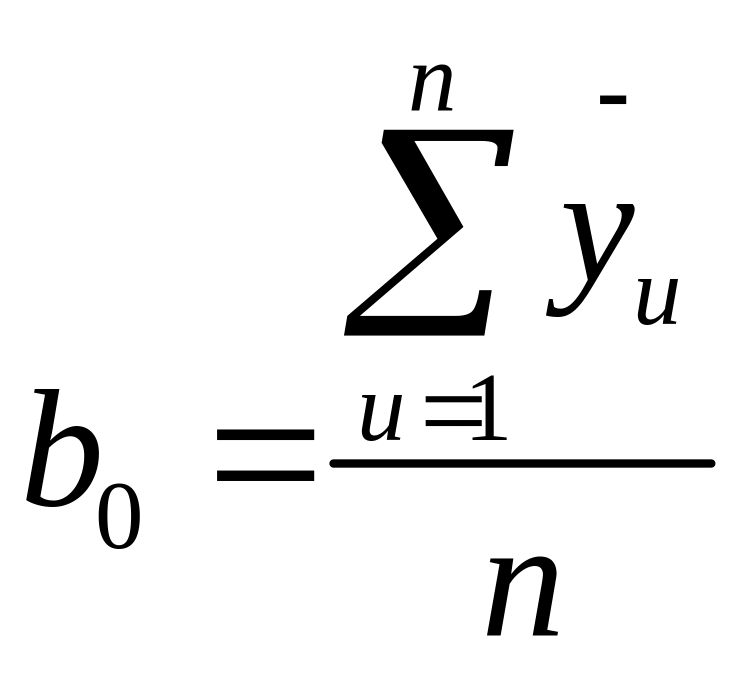. (2.5)

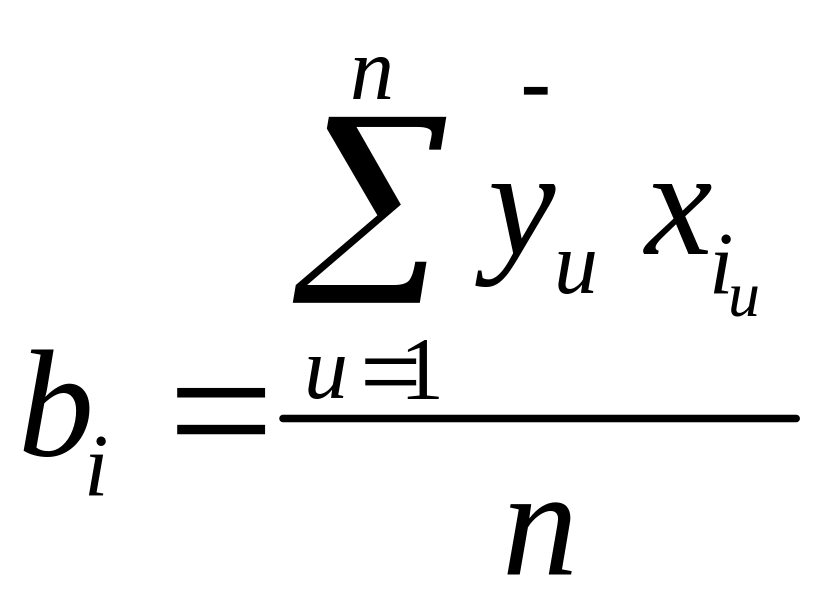. (2.6)

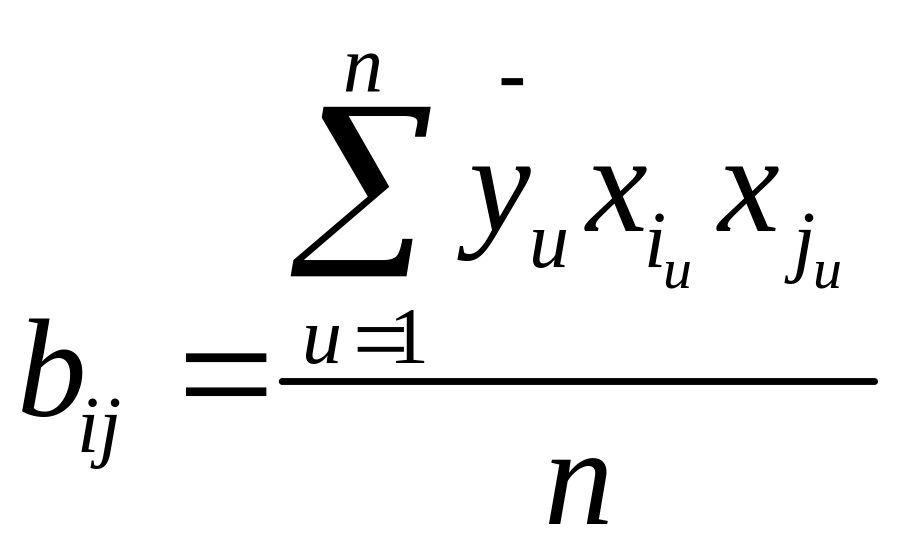. (2.7)

Перевірка адекватності лінійної моделі виконується за допомогою критерію Фішера. Адекватність обґрунтована, якщо виконується нерівність

, (2.8)

де - розрахункове значення відгуку в -му досвіді;

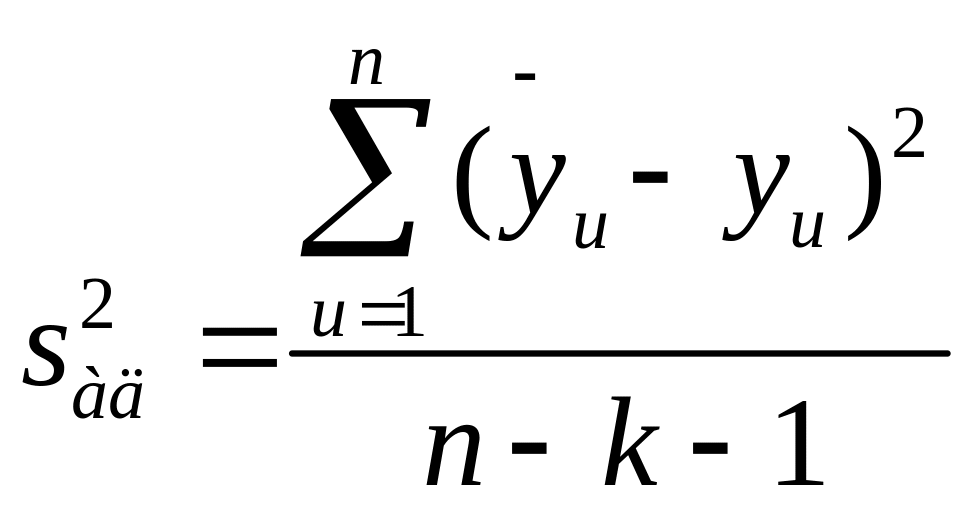, (2.9)

- критерій Фішера при 5%-ном рівні значущості;

- число мір свободи дисперсії адекватності;

- число мір свободи дисперсії відтворюваності.

Оцінка значущості коефіцієнта регресії проводиться за допомогою критерію Стьюдента. Коефіцієнт вважається значущим, якщо виконується нерівність

, (2.10)

де - 5%-ная точки розподілу Стьюдента з мірами свободи.

Якщо в ДФЕ коефіцієнти при взаємодіях не рівні нулю, то знайдені за наслідками дослідів вибіркові коефіцієнти регресії будуть оцінками для сумісних ефектів:

.

3.1.2 Постановка завдання

Досліджується процес дистиляції сировини в апараті періодичної дії. Мета дослідження - визначити залежність виходу продукту (у відсотках від завантаженої в агрегат сировини) від швидкості і кінцевої температури нагріву сировини. Вивчення наявних відомостей про процес дозволили встановити технологічно розумні межі, в яких можуть змінюватися чинники: кінцева температура - від ¹ до ; швидкість нагріву - від до , а також ізотермічна витримка при кінцевій температурі що змінюється в діапазоні від до хв.

План і результати дослідів для даного прикладу приведені в табл. 3.2.1 і 3.2.2.

Необхідно виконати

а) Для кожного плану експерименту:

- кодування чинників;

- перевірку відтворюваності дослідів;

- перевірка адекватності лінійної моделі;

- розрахунок коефіцієнтів регресії;

- оцінку значущості коефіцієнтів регресії;

- записати отримане рівняння регресії.

б) Порівняти отримані рівняння регресії.

Таблиця 3.2.1 - Розширена матриця планування повного експерименту чинника типу

Дослід
1	‑	‑	‑	+	+	+	‑
2	+	‑	‑	‑	‑	+	+
3	‑	+	‑	‑	+	‑	+
4	+	+	‑	+	‑	‑	‑
5	‑	‑	+	+	‑	‑	+
6	+	‑	+	‑	+	‑	‑
7	‑	+	+	‑	‑	+	‑
8	+	+	+	+	+	+	+

Таблиця 3.2.2 - Розширена матриця планування експерименту чинника типу (напіврепліка)

Дослід
1	-	-	+
2	+	-	-
3	-	+	-
4	+	+	+