Лабораторная работа № 1

по курсу «Синтез систем бортовых алгоритмов функциональных задач ЛА»

на тему «Вычисление параметров АММ движения управляемой ракеты»

Цель работы: познакомиться с аппроксимирующей математической моделью движения управляемой ракеты класса «воздух-воздух» являющейся частью БОСЭС дальнего воздушного боя истребителей. Научиться вычислять параметры этой модели.

Теоретическая часть

1. Описание математической модели движения управляемой ракеты.

В качестве представителя реальной управляемой ракеты (УР) класса «воздух-воздух» в работе используется зонная математическая модель (ЗММ) движения ракеты. Она является траекторной моделью. В ней подробно моделируются аэродинамические характеристики ракеты. Работа двигателя ракеты представлена функциональной зависимостью от условий полета ракеты. Попадание ракеты в некоторую окрестность самолета-цели интерпретируется как поражение цели при условии, что соблюдены ограничения на фазовые координаты ракеты на протяжении всего времени управляемого полета ракеты к цели. Такие модели разрабатываются под конкретный тип ракет (класса «воздух-воздух») и утверждаются (сертифицируются) главным конструктором ракеты. Поэтому можно утверждать, что эксперименты с такой моделью аналогичны экспериментам с реальным образцом ракеты при исследовании ее зон возможных пусков (т.е., в нашем случае, при расчете предельных дальностей пуска ракеты).

Будем описывать процесс наведения управляемой ракеты на самолет-цель при следующих допущениях:

1. полет ракеты происходит только под действием тяги двигателя, сил лобового и индуктивного аэродинамического сопротивления и силы тяжести;

2. двигатель ракеты создает постоянную тягу 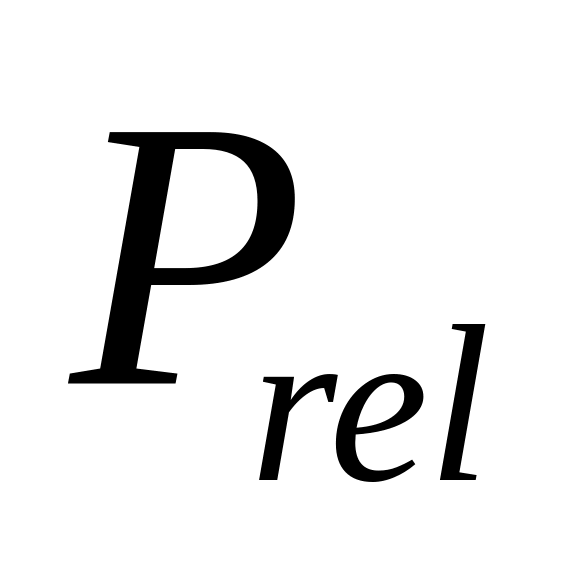(за которую принято отношение средней тяги двигателя ракеты к средней массе ракеты за время работы двигателя ракеты) только в течение секунд с момента старта ракеты:

3. воздействие сил лобового и индуктивного аэродинамического сопротивления на полет ракеты учитывается соответственно двумя постоянными параметрами (обобщенные коэффициенты лобового и индуктивного сопротивления), зависящими от условий старта ракеты:

4. контур наведения ракеты полагается безынерционным, обеспечивая мгновенную отработку заданных управляющих сигналов;

5. окончание наведения ракеты наступает при выполнении в некоторый момент времени хотя бы одного условия: 1) попадание ракеты в некоторую окрестность цели 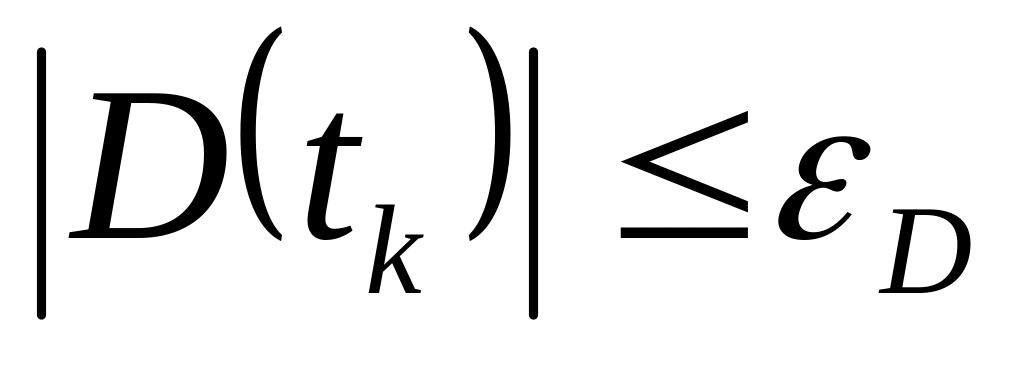, где 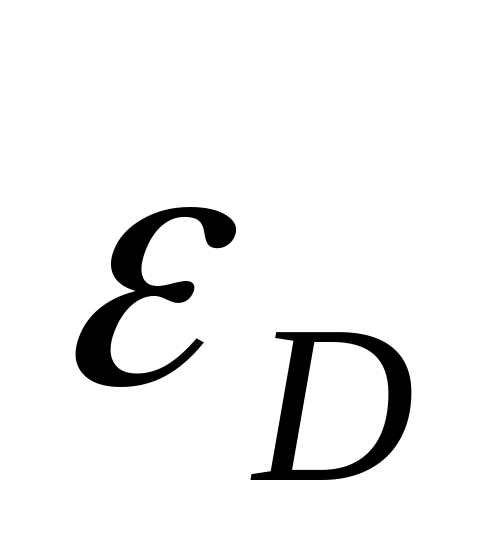- радиус этой окрестности (малая величина), 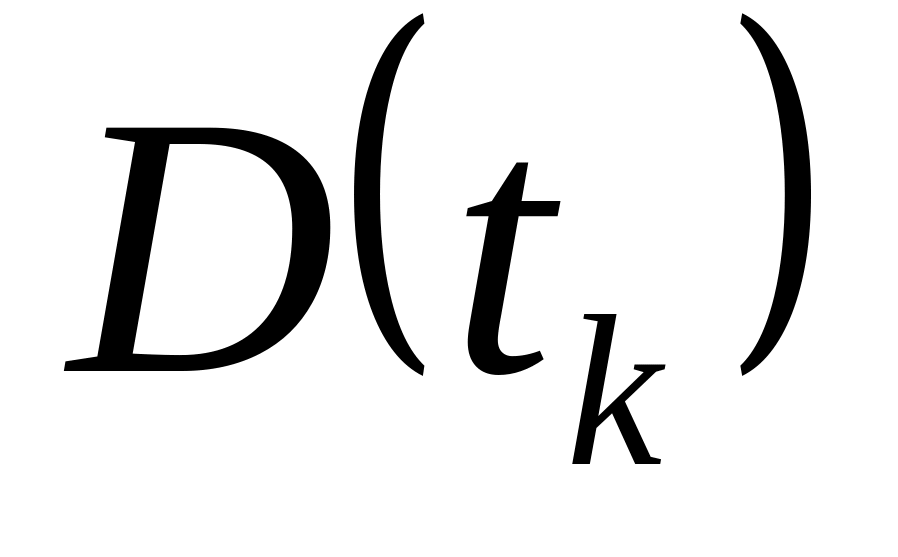- дальность «ракета-цель» в момент ; 2) снижение скорости полета ракеты до скорости цели (в данной работе принято ).

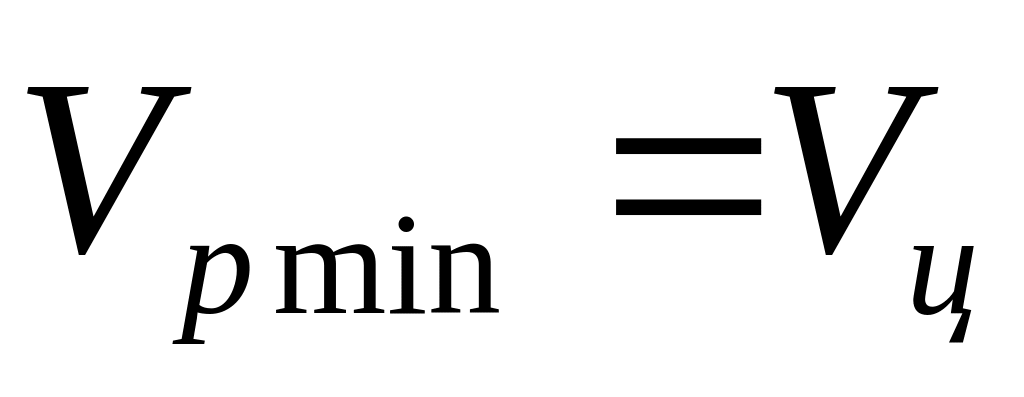Движение центра масс ЛА в пространстве (в земной системе координат) в случае полета без скольжения с неизменной массой ЛА описывается следующей системой дифференциальных уравнений [1]:

(1)

где – ускорение силы тяжести; – тангенциальная и нормальная скоростная перегрузка летательного аппарата (ЛА); – тяга двигателя ЛА; – сила лобового сопротивления ЛА; – аэродинамическая подъемная сила ЛА; – масса ЛА; – скоростной угол крена ЛА; – скорость полета ЛА; – углы поворота и наклона траектории полета ЛА; – декартовые координаты ЛА в земной системе координат. Следует заметить, что здесь положительный отсчет угла выполняется по часовой стрелке. В системе (1) фазовыми координатами являются переменные ; управляющими сигналами – . Принята безынерционная отработка управляющих сигналов.

Воспользуемся квадратичной аппроксимацией поляры ракеты:

,

где ; – скоростной напор; – плотность воздуха на заданной высоте . Управляющими сигналами ракеты выберем в системе (1) величины , Величина при (скоростях более 300 м/с) может быть аппроксимирована зависимостью . Тогда система дифференциальных уравнений полета ракеты на основе системы (1) будет иметь вид:

(2)

где – соответственно скорость и высота полета ракеты; – остальные декартовые координаты ракеты в земной системе координат; – углы поворота и наклона траектории ракеты (положительный отсчет угла – по часовой стрелке); управляющие сигналы ракеты (в соответствии с методом пропорциональной навигации)

– вектор дальности «ракета-цель»; – вектор скорости полета самолета-цели; – навигационный коэффициент модели ракеты; ограничение управляющего сигнала ракеты ; – компоненты угловой скорости вращения линии дальности «ракета-цель» в связанной с ракетой системе координат (поворот этой системы координат относительно земной только на углы поворота и наклона траектории полета ракеты – полускоростная система координат ):

вектор угловой скорости линии дальности «ракета-цель» в земной системе координат

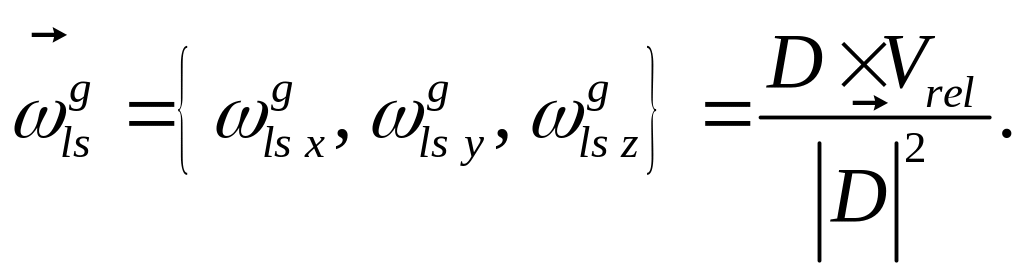
В уравнениях (2) используется экспоненциальная зависимость (таблица стандартной атмосферы, ГОСТ 4401-81) плотности воздуха от высоты полета летящего объекта: где – высота полета (в метрах), , .

Назовем эту математическую модель движения ракеты аппроксимационной (АММ) и введем для нее обозначение , где:

– обобщенный коэффициент тяги двигателя ракеты (отношение средней тяги двигателя ракеты к средней массе ракеты за время работы двигателя ракеты),

– продолжительность работы однорежимного двигателя ракеты (продолжительность активного участка),

– обобщенный коэффициент лобового сопротивления ракеты соответственно на активном и пассивном (с отработавшим двигателем) участке ее полета,

– обобщенный коэффициент индуктивного сопротивления ракеты соответственно на активном и пассивном (с отработавшим двигателем) участке ее полета.

Параметры АММ зависят от следующих переменных в момент старта ракеты: от типа ракеты, высоты и скорости полета истребителя, пускающего ракету. Они полагаются константами на протяжении всего времени полета ракеты.

Эту модель удобно использовать при решении задачи сопровождения УР противника неизвестного типа и расчета для нее максимальной (Дmax), тактической (Дтп) и гарантированной (Дгп) дальностей пуска ракеты (т.е. пуск ракеты по неманеврирующей цели (Дmax), и цели, совершающей маневры тактический (Дтп) или гарантированный (Дгп) отворот).