Дайте определение ковариации.
Ковариа́ция (корреляционный момент) в теории вероятностей и математической статистике мера линейной зависимости двух случайных величин.
Определение
Пусть X,Y — две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда их ковариация определяется следующим образом:
,
в предположении, что все математические ожидания E в правой части определены.
Замечания
Если
,
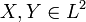то есть имеют конечный второй момент,
то ковариация определена и конечна.В гильбертовом пространстве несмещённых случайных величин с конечным вторым моментом
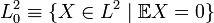ковариация
имеет вид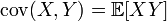 
и
играет роль скалярного
произведения.
11. Коррелированность и некоррелированность - это свойство пары (случайных величин, наборов данных). Определяется по величине коэффициента корреляции (есть разные варианты).
12. Генеральная совокупность – все множество имеющихся объектов.
Выборка – набор объектов, случайно отобранных из генеральной совокупности.
Объем генеральной совокупности N и объем выборки n – число объектов в рассматривае-мой совокупности.
Виды выборки:
Повторная – каждый отобранный объект перед выбором следующего возвращается в генеральную совокупность;
Бесповторная – отобранный объект в генеральную совокупность не возвращается.
13. выборочным средним называется случайная величина
.
Пусть 
—
случайная величина, определённая на
некотором вероятностном
пространстве.
Тогда
где символ M обозначает математическое ожидание
Среднеквадратическое отклонение:
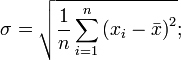
стандартное отклонение (несмещённая оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания):
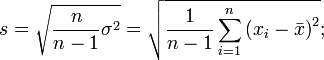
где 
— дисперсия; 
— i-й
элемент выборки; 
—
объём выборки; 
— среднее
арифметическое выборки:
14. Оценка О называется несмещенной оценкой параметра О, если ее мат. ожидание равно оцениваемому параметру: М(О)= О. В противном случае оценка называется смещенной.
Оценка О* называется эффективной оценкой параметра О, если ее дисперсия Д(О*) меньше дисперсии любой другой альтернативной несмещенной оценки при фиксированном объёме выборки n, т.е. Д(О*)= Дмин.
Оценка О*n называется состоятельной оценкой параметра О, если О*n сходится по вероятности к оцениваемому параметру О при n-∞. Другими словами, состоятельной называется такая оценка, которая дает истинное значение при достаточно большом объёме выборки вне зависимости от значений входящих в нее конкретных наблюдений.
15.
16. Точечной оценкой О* параметра О называется числовое значение этого параметра, полученное по выборке объёма n.
Точечная оценка может быть дополнена интервальной оценкой- интервалом (О1;О2), внутри которого с наперед заданной вероятностью у находится точное значение оцениваемого параметра О.
17. Гипотеза Н0, подлежащая проверке, -нулевая гипотеза. Гипотеза Н1, которая будет приниматься, если отклоняется Н0- альтернативная.
18. Вероятность совершить ошибку 1-го рода принято обозначать буквой а и ее называют уровнем значимости.
Статистический критерий- СВ К, котторая служит для проверки нулевой гипотезы.
19. Важнейшей целью статистики является изучение объективно существующих связей между явлениями. В ходе статистического исследования этих связей необходимо выявить причинно-следственные зависимости между показателями, т.е. насколько изменение одних показателей зависит от изменения других показателей.
Существует две категории зависимостей (функциональная и корреляционная) и две группы признаков (признаки-факторы и результативные признаки). В отличие от функциональной связи, где существует полное соответствие между факторными и результативными признаками, в корреляционной связи отсутствует это полное соответствие.
Корреляционная связь - это связь, где воздействие отдельных факторов проявляется только как тенденция (в среднем) при массовом наблюдении фактических данных. Примерами корреляционной зависимости могут быть зависимости между размерами активов банка и суммой прибыли банка, ростом производительности труда и стажем работы сотрудников.
20. Суть регрессионного анализа сводится к установлению уравнения регрессии, т.е. вида кривой между случайными величинами (аргументами x и функцией y ), оценке тесноты связей между ними, достоверности и адекватности результатов измерений.