3) Коэффициент детерминации

По свойству: , он показывает, что вариация результативного признака Y на 41,2% объясняется вариацией фактора X. То есть, изменения количества автомобилей в регионах на 41,2% обусловлены колебаниями размеров среднедушевых доходов населения, а в остальном – на 58,8% обусловлены колебаниями и изменениями других факторов и условий.

Итак, полученный линейный коэффициент корреляции , коэффициент регрессии b₁= 0,036 и коэффициент детерминации свидетельствуют, что линейная зависимость количества легковых автомобилей и среднедушевых доходов населения в регионах положительная, средняя, умеренная. Подтвердилось предположение о том, что и другие факторы оказывают существенное влияние на количество легковых автомобилей в регионах.

4) Средний коэффициент эластичности:

Для линейной регрессии: . Средний коэффициент эластичности показывает, что в среднем при повышении размера среднедушевого дохода в месяц на 1% от своего среднего значения количество автомобилей увеличивается на 0,317% от своего среднего значения. Эластичность количества автомобилей по размеру среднедушевого дохода невелика, что вполне согласуется с экономической теорией, т.к. автомобиль не относится к предметам первой необходимости, а потому небольшое увеличение или уменьшение доходов не влечет за собой резкого повышения или понижения спроса на автомобили.

Проверим правильность вычислений: (см. табл., сумма в 8-м столбце действительно равна нулю).

5) Оценка статистической значимости коэффициентов регрессии и коэффициента корреляции

Оценим статистическую значимость полученных коэффициентов регрессии b₀ и b₁, коэффициента корреляции r_ух с помощью t-критерия Стьюдента на уровне значимости α = 0,05. Эта проверка проводится по единой схеме, с помощью статистических гипотез. Выдвигается нулевая гипотеза Н₀ о случайной природе полученного коэффициента, о незначимом его отличии от нуля, то есть гипотеза Н₀ состоит в том, что коэффициент=0. Альтернативная ей гипотеза Н₁ состоит в том, что неслучайно, то есть полученный коэффициент статистически значим. Чтобы опровергнуть гипотезу Н₀ и подтвердить гипотезу Н₁ должно выполняться неравенство на уровне значимости α и с (n–2) степенями свободы, где n – количество наблюдений, уровень значимости  – вероятность совершить ошибку, опровергнув гипотезу Н₀, когда она верна.

Для b₁: Н₀: b₁=0, Н₁: .

Рассчитаем стандартную ошибку коэффициента регрессии b₁ – . Потребуется сделать промежуточные вычисления: подставляя фактические значения х_i в уравнение регрессии найдем теоретические (смоделированные) значения , затем вычислим разность между фактическими и смоделированными значениями, т.е. остатки , затем возведём остатки в квадрат е_i² и просуммируем; результаты представлены в расчетной таблице. Теперь подставим необходимые данные в формулу для расчёта :

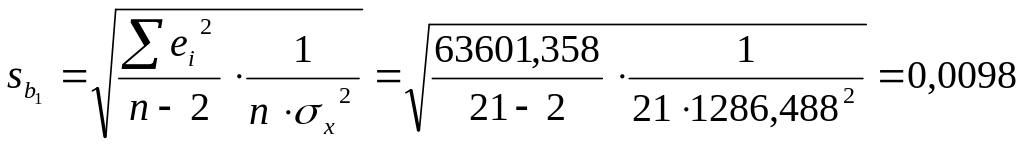
и t-статистики по модулю: .

Или

Затем сравним наблюдаемое значение с табличным значением t-критерия Стьюдента. Табличное значение по таблице распределения Стьюдента на уровне значимости α=0,05 с n–2=21–2=19 степенями свободы: t_табл=2,093 или с помощью функции СТЬЮДРАСПОБР(α; ν)= 2,093. Наблюдаемое значение t-статистики превышает табличное значение t-критерия: 3,646 > 2,093, то есть выполнено неравенство , а значит, Н₀ о случайной природе полученного коэффициента отвергается, и принимается альтернативная ей гипотеза Н₁, свидетельствующая в 95% случаев о статистической значимости полученного коэффициента регрессии b₁. Т.о., можно считать, что предполагаемая зависимость количества легковых автомобилей от размера среднедушевых доходов подтвердилась и статистически установлена.

Для b₀: Н₀: b₀=0, Н₁: .

Рассчитаем стандартную ошибку коэффициента регрессии b₀ – . Все необходимые цифры уже имеются в расчетной таблице, подставим эти данные в формулу: 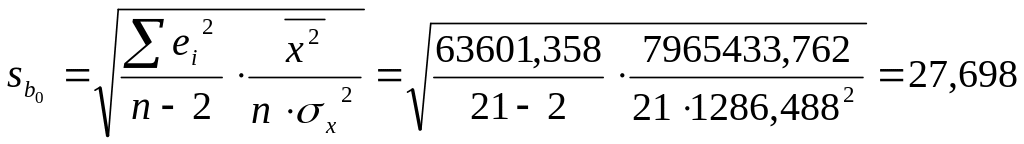, а затем рассчитаем t-статистику по модулю: .

Сравнивая рассчитанное значение с табличным значением t-критерия Стьюдента на уровне значимости α = 0,05 с n–2=21-2=19 степенями свободы: t_табл=2,093, можно сделать вывод о статистической значимости полученного коэффициента регрессии b₀ в 95% случаев.

Для r_ух: Н₀: r_ух=0, Н₁: .

Для этого рассчитаем стандартную ошибку коэффициента корреляции r_ух – : 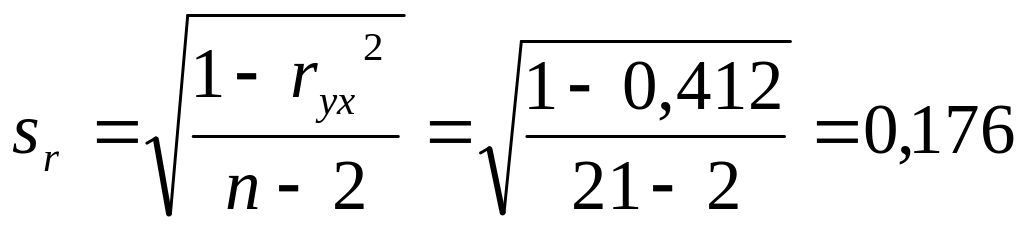и t-статистику по модулю: .

Сравнивая рассчитанное значение с табличным значением t-критерия Стьюдента на уровне значимости α=0,05 с n–2=21-2=19 степенями свободы: t_табл=2,093, можно сделать вывод о статистической значимости полученного коэффициента корреляции r_ух в 95% случаев, можно считать, что предполагаемая зависимость количества легковых автомобилей от размера среднедушевых доходов подтвердилась и статистически установлена.

Проверим правильность вычислений: , действительно 3,646²=3,646².