9.2 Сумматоры, интеграторы и дифференциаторы на базе усилителей

Различают инвертирующие и неинвертирующие сумматоры [3,15]. Принципиальная схема инвертирующего сумматора приведена на рис. 9.7.

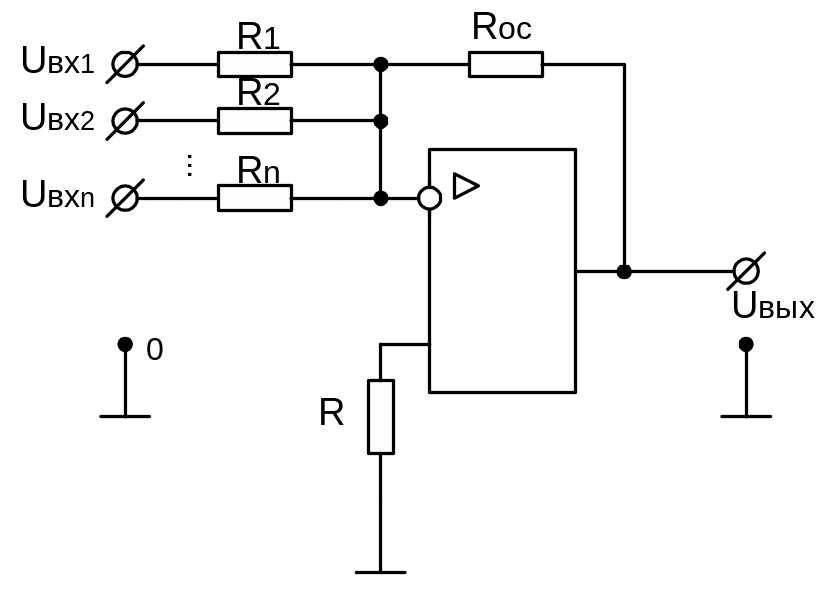
Рисунок 9.13 — Схема инвертирующего сумматора

Сигналы можно правильно суммировать только на линейном участке амплитудной характеристики «1–1’» ОУПТ (см. рис.9.8).

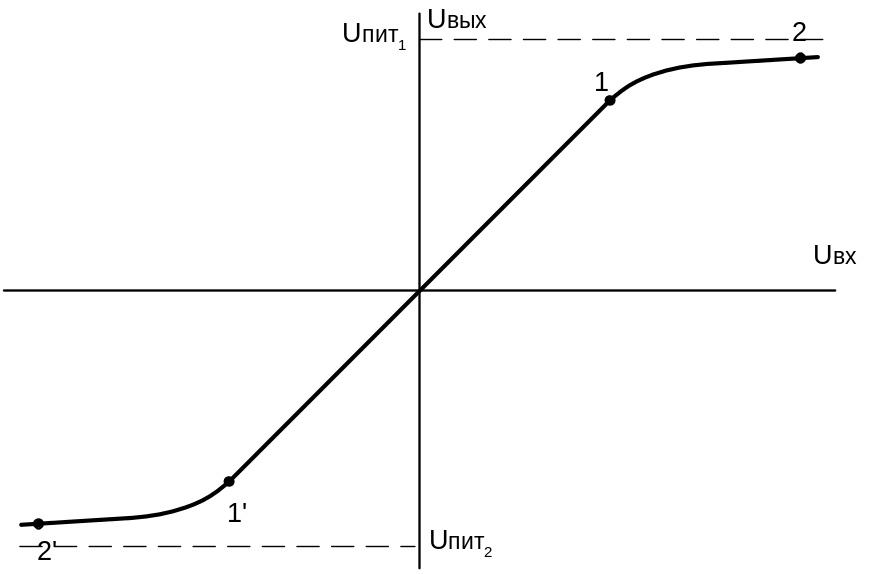
Рисунок 9.14 — Амплитудная характеристика ОУПТ

На участке 1–1’ режим работы ОУПТ линейный, где применим принцип суперпозиции, и выходное напряжение можно рассматривать как сумму реакций от входных сигналов:

Наихудшее согласование внутреннего сопротивления источника сигнала со входом усилителя будет на том входе, где самый большой коэффициент усиления , поэтому для этого входа обеспечивают требуемое согласование с источником, а для всех остальных входов согласование получится лучшим. Выбор резисторов і аналогичный инвертирующему усилителю. Величина резистора R определяется из условия:

Величина выходного сопротивления сумматора определяется аналогично ранее рассмотренным схемам:

.

где , а

Принципиальная схема неинвертирующего сумматора приведена на рис. 9.9.

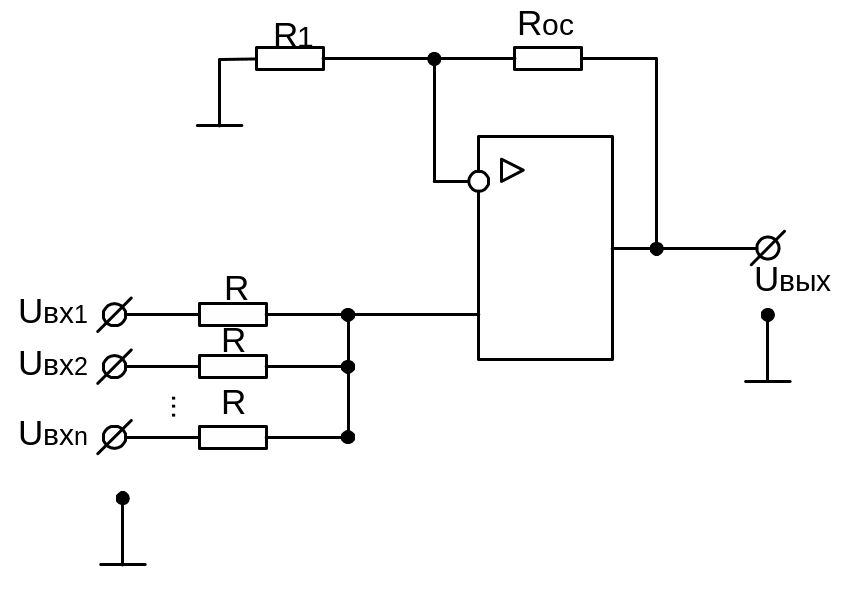
Рисунок 9.15 — Схема неинвертирующего сумматора

В данной схеме коэффициенты передачи по всем входам одинаковы и определяются выражением:

Выходное напряжение для линейного режима работы определяется выражением:

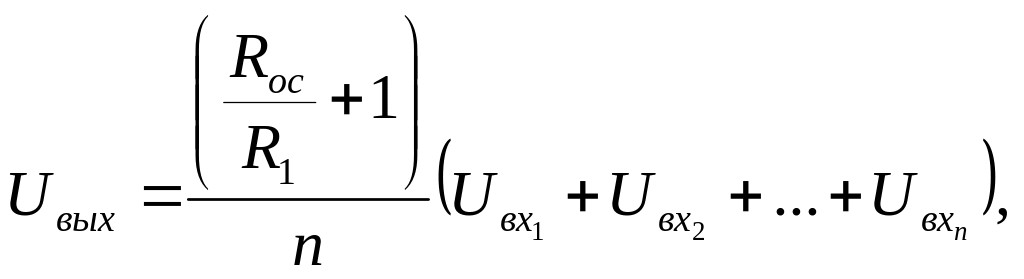
где n — количество входов сумматора.

Резистор R не оказывает влияние на коэффициенты передачи сумматора . Входное и выходное сопротивления усилителей определяются аналогично рассмотренному выше неинвертирующему усилителю. Входные резисторы сумматора R должны быть много меньше (в 5–10 раз) входного сопротивления усилителя .

Основной недостаток схемы: коэффициенты передачи по всем входам одинаковы. Для обеспечения их регулирования может быть предложена постановка на каждый вход потенциометров, или использования схемы инвертирующего сумматора с инвертором.

16. Интеграторы. Дифференциаторы. Логарифматоры и антилагорифматоры.

Принципиальная схема интегратора на ОУПТ представлена на рис. 9.10 [3,15].

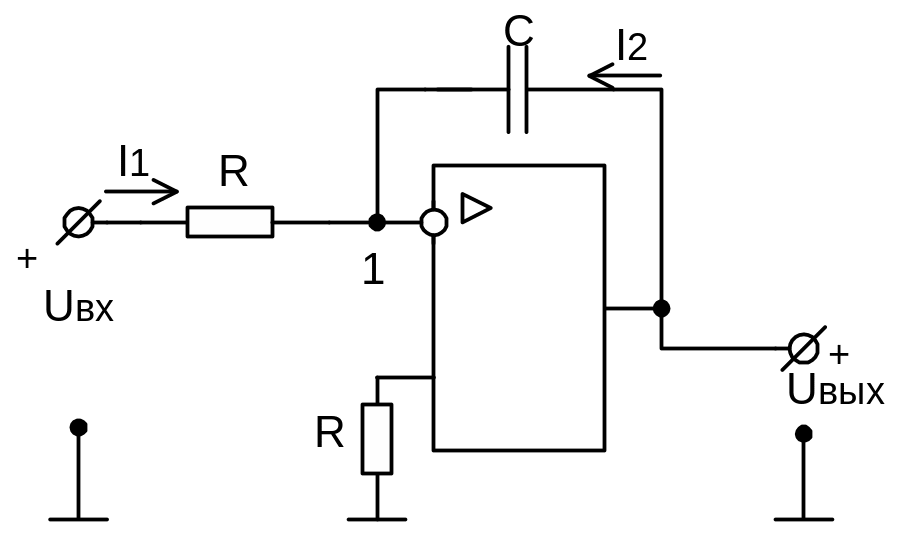
Рисунок 9.16 — Схема интегратора на ОУПТ

Покажем, что данная схема является интегратором. Запишем первый закон Кирхгофа для точки 1, пренебрегая входным током усилителя, считая его идеальным.

; .

С учетом того, что потенциал точки 1 равен нулю (виртуальный нуль), получим:

; .

Тогда получим:

; ;

где p=j. Отсюда следует:

.

Окончательно, переходя из операторной формы, имеем

при нулевых начальных условиях.

Чем больше постоянная времени интегратора =RC, тем меньше коэффициент передачи интегратора. Начальные условия легко учитывать в этой схеме путем смещения напряжения на на требуемую величину с помощью схемы установки нуля (см. раздел 9.3).

Пусть и равно +1В, начальные условия нулевые. Поскольку интеграл от постоянной величины представляет линейную функцию времени, а также учитывая инвертирующее свойство усилителя, получим прямую, расположенную в IV квадранте (см. рис.9.11 а). При увеличении (уменьшении) входного сигнала изменяется крутизна этой прямой пропорционально U_вх при . Интегрирование возможно до тех пор (время t_max при U_вх=+1 В), пока выходное напряжение не превышает допустимого значения из амплитудной характеристики усилителя (см. рис. 9.11 а, t_max при U_вх=+1 В). При отрицательных входных сигналах характеристики аналогичны, но располагаются в I квадранте (см. рис.9.11 б). При изменение постоянной времени  приводит к изменению крутизны характеристики преобразования (см. рис. 9.12). Включив последовательно два интегратора и подав на вход первого константу, на выходе второго получим квадратичную параболу.

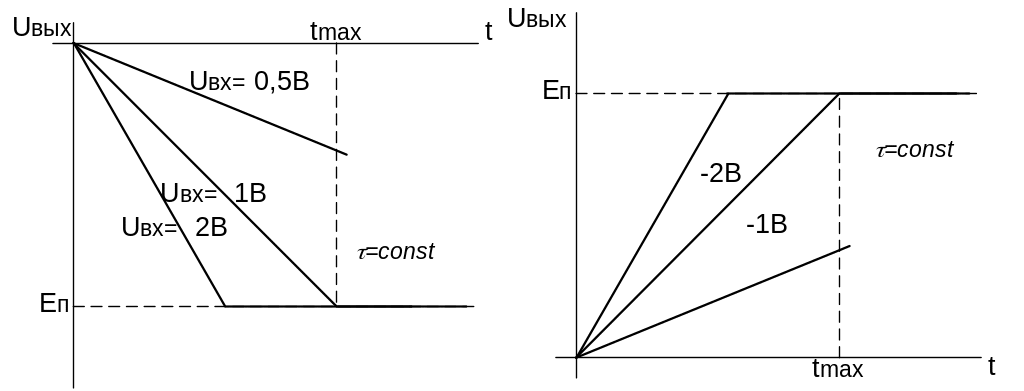
а) б)

Рисунок 9.17 — Зависимость выходного напряжения интегратора от U_вх при

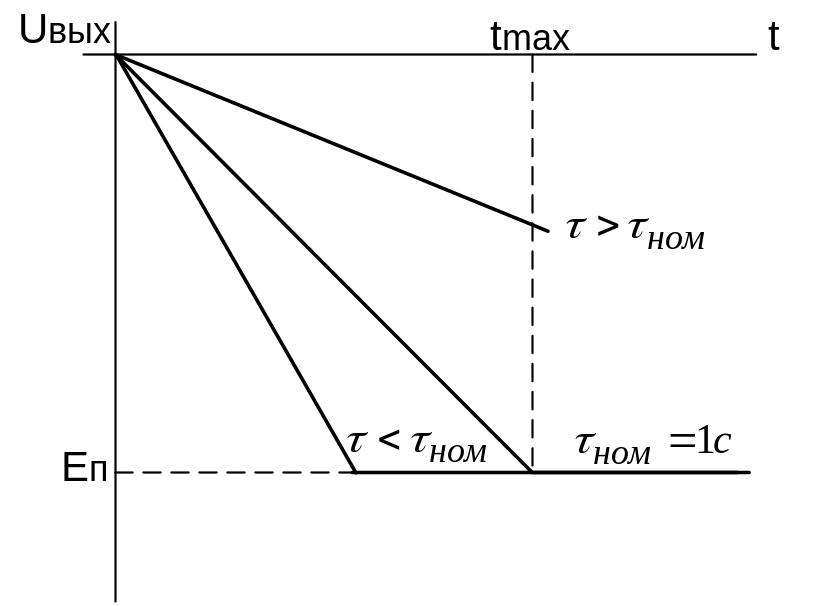
Рисунок 9.18 — Зависимость выходного напряжения интегратора от постоянной времени при

Следовательно, с помощью интегратора можно получать степенные функции n–порядка при количестве интеграторов равно n.

Принципиальная схема дифференциатора на ОУПТ представлена на рис. 14.13.

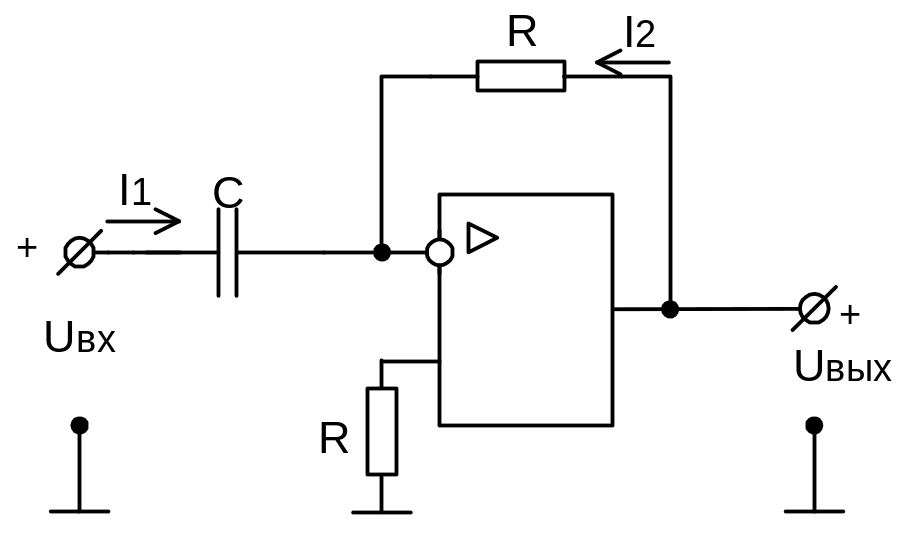
Рисунок 9.19 — Схема дифференциатора на ОУПТ

Запишем уравнение первого закона Кирхгофа аналогично интегратору, пренебрегая входным током усилителя.

Откуда,

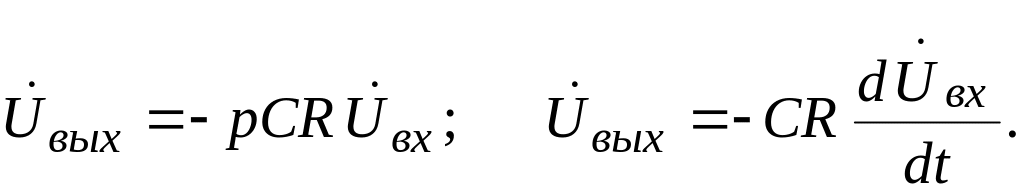
Следовательно, данная схема является дифференцирующей. При на выходе получим , так как производная от константы равна нулю. При подаче на вход схемы линейно возрастающего напряжения на выходе получим константу, пропорциональную крутизне входного напряжения.