1. Материальный баланс потока (уравнение неразрывности потока).

Допустим, что в сечении /—/ трубы (рисунок 12) все частицы имеют среднюю скорость w, тогда за единицу времени они пройдут путь, равный w, и переместятся в сечение //—//.

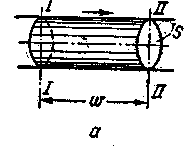
рисунок 12

Если скорости частиц жидкости не изменяются во времени, ее движение считается установившимся. При установившемся движении в каждом сечении потока постоянны не только скорость, но и расход, температура, давление и плотность жидкости. Вместе с тем при установившемся движении скорости потока могут изменяться в пространстве, при переходе жидкости от одного сечения к другому. Рассмотрим установившееся движение жидкости, ограниченной стенками любой формы, например движение в трубе переменного сечения (рисунок 13).

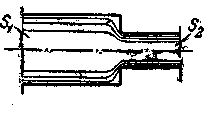
рисунок 13

Движущаяся жидкость сплошь заполняет трубу, в которой, таким образом, нет пустот и разрывов потока. При переходе от сечения S₁ к сечению S₂ скорость жидкости будет изменяться, но по закону сохранения вещества количество жидкости, поступающей в единицу времени через сечение S₁ будет равно количеству ее, протекающему через сечение S₂, т.е. расход жидкости останется постоянным. В том случае, если эти количества не были бы равны (например, ели поступающее через сечение S₁ количество жидкости превышало бы количество, проходящее через сечение S₂), жидкость накапливалась бы в трубе между сечениями S₁ и S₂ и здесь происходило бы возрастание давление и плотности, что при установившемся течении невозможно.

Принимая массовые скорости жидкости в сечениях S₁ и S₂ равными соответственно и можно записать:

(1.42) [10]

или

(1.43) [10]

Для несжимаемой жидкости плотности потоков равны и уравнение (1.43) имеет вид:

(1.44) [10]

Уравнения (1.42), (1.43), (1.44) [10] представляют собой уравнение неразрывности потока или материальный баланс потока.

Согласно этим уравнениям, средние скорости жидкости в различных сечениях трубопровода обратно пропорциональны площадям этих сечений. При расширении потока его средняя уменьшается и наоборот. Произведение скоростей на сечение, т.е. расход жидкости при установившемся движении величина постоянная.

2. Удельная энергия жидкости.

Жидкость, независимо от того, находится ли она в состоянии покоя или движения, обладает некоторым запасом энергии, равным сумме внутренней энергии, потенциальной и кинетической энергии.

Удельная (полная) энергия состоит:

(1.45) [10]

где внутренняя энергия, Дж;

рV – потенциальная энергия давления жидкости, Дж;

mgz – потенциальная энергия положения жидкости, Дж;

кинетическая энергия жидкости, движущейся со скоростью , Дж.

Внутренняя энергия представляет собой энергию молекул жидкости, всегда совершающих поступательные и вращательные движения и поэтому обладающих кинетической энергией этих движений.

Потенциальная энергия жидкости состоит из потенциальной энергии давления и потенциальной энергии положения.

Сумма внутренней и потенциальной энергий давления называется энтальпией (теплосодержанием) и обозначается через I.

(1.46) [10]

Соответственно полная энергия жидкости выражается равенством:

(1.47) [10]

Удельная энергия жидкости, т.е. энергия 1 кг жидкости, может быть найдена делением обеих частей уравнения (1.45) или уравнения (1.47) на массу жидкости m.

, (1.48) [10]

где u – внутренняя энергия 1 кг жидкости, Дж/кг;

v – объём, занимаемый 1 кг жидкости, м³/кг;

i – энтальпия 1 кг жидкости, Дж/кг.