3.2. Електропровідність металів

У металах і їх сплавах є велика кількість вільних, тобто не зв'я­заних з конкретними атомами, електронів. В кристалі об'ємом 1 см³ міститься 10²³ - 10²² атомів. Якщо прийняти, що атоми в металі іонізовані однократно, то концентрація вільних електронів рівна концентрації атомів. Ці вільні електрони та іони кристалічної ґрат­ки перебувають у безперервному хаотичному русі. Іони тільки коливаються навколо своїх положень рівноваги, а вільні електро­ни можуть переміщатися у всьому об'ємі металу. Розміри елект­ронів дуже малі порівняно з відстанями між іонами ґратки, а хао­тичний рух подібний до руху молекул газу. Інколи їх називають "електронним газом".

Гіпотеза про електронний газ підтверджується експеримента­льно, а саме:

► За тривалого протікання струму в колі, складеному з прові­дників різних металів, атоми одного металу не проникають в інші, тобто атоми металу не переміщуються разом зі струмом.

► За раптової зупинки провідника, який швидко рухався, вільні електрони за інерцією продовжують деякий час рухатись і на кін­цях загальмованого провідника виникає різниця потенціалів.

Якщо в металі відсутнє електричне поле, то рух електронів є хаотичний, тобто в будь-який момент швидкості окремих елект­ронів спрямовані в різні напрями (рис. 3.2).

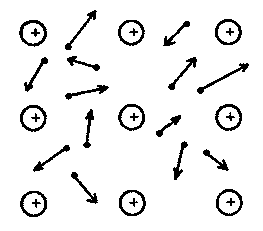
Рис. 3.2. Напрям руху електронів за відсутності поля

Такий рух не викликає струму, тому що внаслідок повної хао­тичності в кожному напрямі буде рухатись стільки ж електронів, як і в протилежному. Геометрична сума швидкостей v_m електро­нів для достатньо великого об'єму металу дорівнює нулю і струм відсутній.

Якщо ж ми прикладемо до кінців провідника різницю потенціа­лів, тобто створимо в середині металу градієнт електричного поля, то на кожний електрон діятиме сила F = Ее. Електрон з масою т, розташований в "пустому" міжіонному просторі, який не гальмує його руху, отримає пришвидшення в напрямку Е, яке дорівнює:

а - F/m = Е е/т,

де відношення е/т складає 1,759 · 10¹¹ Кл/кг. Через певний час t компонента швидкості електрона в напрямі поля становитиме

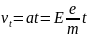
а сумарна швидкість дорівнюватиме сумі швидкостей v_m і ν_e.

Електрон у процесі руху буде наштовхуватися на іони ґратки.

Після кожного співударяння швидкість електрона спадає до нуля,

потім знову зростає з попереднім пришвидшенням. Таким чином,

v буде змінюватись з часом t згідно з пилкоподібним графіком,

схематично зображеним на рис. 3.3.

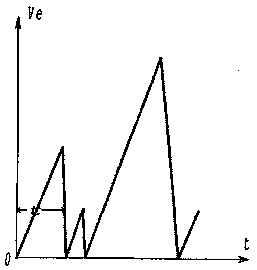
Рис. 3.3. Графік зміни в часі швидкості v_e електрона в металі (схематично)

Експериментально встановле­ но, що середня довжина шляху ві­ льного пробігу електрона в мета­ лах високої провідності становить в нормальних умовах 10 ⁴ – 10 ⁵ мм, а при дуже низьких темпера­ турах - значно більше, тобто еле­ ктрони рухаються без зіткнень по­ рядку сотень параметрів ґратки. Найбільше значення швидкості v_e даного електрона в кінці кожного періоду пришвидшення триваліс- тю τ (час вільного пробігу елект- рона) дорівнює:

є

_т '

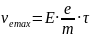
а середня його швидкість за час τ становить

(3.5)

За нормальної температури швидкість v_m для металів складає приблизно 10⁵ м/с, а швидкість ν_e- порядку 10^{- 4} м/с, тобто ν_m>>ν_e . Тому середнє значення τ_сер для всіх електронів дорівнює

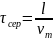
де l - середня довжина вільного пробігу електрона. Підставивши значення у (3.5), отримаємо середнє значення v_{e cep} швидкостей v_e для всіх електронів:

(3.6)

Наявність компоненти v_e створює впорядкований рух зарядів в напрямку градієнта електричного поля. Якщо у формулу (3.3) за­мість g підставити заряд електрона є, замість v_e- вираз v_{e cep} з (3.6), отримуємо:

(3.7)

Згідно з атомно-кінетичною теорією ідеальних газів кінетична енергія електронів лінійно зростає з температурою:

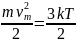
де k - стала Больцмана, Т - абсолютна температура. Підстанов­ка ν_m з (3.8) у (3.7) дає:

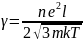(3.9)

або 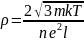(3.10)