Зміст

ВСТУП 2

Розділ 1. Методика вивчення визначеного інтеграла. 3

1. Задачі, що привели до поняття визначеного інтеграла. 3

2. Означення визначеного інтеграла та його геометричний зміст. 5

3. Критерій інтегровності функції. 6

Розділ 2. Властивості визначеного інтеграла. 8

Розділ 3. Формула Ньютона – Лейбніца. 10

1. Методика введення формули Ньютона – Лейбніца. 10

2. Приклади обчислення інтеграла за формулою Ньютона – Лейбніца. 11

ВИСНОВОК 12

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ 13

ВСТУП

Актуальність теми. За останні роки у соціальному житті суспільства відбулися значні зміни, а отже і у системі освіти. В школах впроваджено дванацятирічну освіту. У зв’язку з цим внесені зміни до навчальних програм та навчальних планів. Це вплинуло на шкільний курс математики, змінився розподіл годин на вивчення окремих розділів та кількість тематичних оцінювань.

Тема «Інтеграл та його застосування» вивчається в 11 класі, тобто у випускному. Тому учні повинні добре засвоїти і вміти застосовувати теоретичний матеріал до розв’язування вправ з даної теми. У цьому році математика є обов’язковим предметом на зовнішньому тестуванні, не залежно від профільності класів.

Мета роботи. Метою роботи є показати, якими особливостями має бути методика вивчення теми «Визначений інтеграл та його застосування».

Предмет дослідження. Предметом дослідження є вивчення визначеного інтеграла та його застосування в середній школі.

Задачі дослідження.

1. Вивчити науково-методичну літературу з предмету дослідження.

2. Охарактеризувати особливості вивчення математики у профільних класах і втілити їх у розробки уроків.

Методи дослідження. Теоретичні – системний аналіз навчально-методичної літератури з проблеми дослідження, розробка уроків.

Емпіричні – вивчення даної теми у профільних класах, застосування у інших науках.

Теоретичне значення роботи полягає в обґрунтуванні методики вивчення даної теми, аналізу підручників та програм з математики для профільних класів.

Практична цінність. Робота може бути використана вчителями математики та студентами для проведення занять з математики.

Розділ 1. Методика вивчення визначеного інтеграла.

1. Задачі, що привели до поняття визначеного інтеграла.

Поняття визначеного інтеграла виникло у зв’язку із розв’язуванням геометричних задач (про обчислення площі криволінійної трапеції) та фізичних (про визначення шляху, пройденого точкою під час прямолінійного руху за її відомою миттєвою швидкістю; роботу змінної сили; масу неоднорідного стержня). Розв’язування їх зводиться до виконання граничного переходу певного типу.

Традиційно склалося так, що в курсах метематичного аналізу вищої школи введення визначеного інтеграла здебільшого пов’язується зі розв’язуванням задачі про визначення площі криволінійної трапеції. Проте в шкільних посібниках і в підручниках для технікумів була спроба покласти в основу означення інтеграла формулу Ньютона – Лейбніца (інтегралом на проміжку називають приріст первісної на цьому проміжку, тобто

).

У чинній шкільній програмі та підручниках прийнято традиційний підхід до запровадження інтеграла у зв’язку із задачею про площу криволінійної трапеції. У шкільному курсі вводиться таке означення інтеграла: відрізок під час розв’язування задачі про площу криволінійної трапеції розбивають на рівних частин; складають скінченну суму добутків значення функції в лівому або правому кінці відрізка розбиття на довжину кожного з відрізків і за шукають границю цієї суми, яку, за означенням, і вважають площею криволінійної трапеції.

З а д а ч а п р о п л о щ у к р и в о л і н і й н о ї т р а п е ц і ї.

Д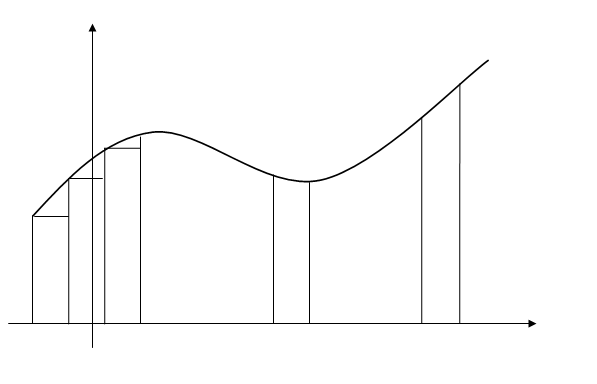 оцільно насамперед звернути увагу учнів на те, що у шкільному курсі геометрії вивчають способи обчислення площ фігур лише певного виду (многокутників, круга і його частин). Виникає запитання: як обчислити площу плоскої фігури, обмеженої будь – якою кривою? мал. 1 Після введення поняття про криволінійну трапецію як фігуру, обмежену відрізком осі , графіком неперервної функції і прямими (мал. 1), відрізок розбивають на рівних частин точками

.

На кожному з відрізків розбиття будують прямокутники з висотою, що дорівнює значенню функції в лівому (або правому) кінці відрізка.

Площу східчастої фігури, що є об’єднанням побудованих прямокутників, визначають як суму

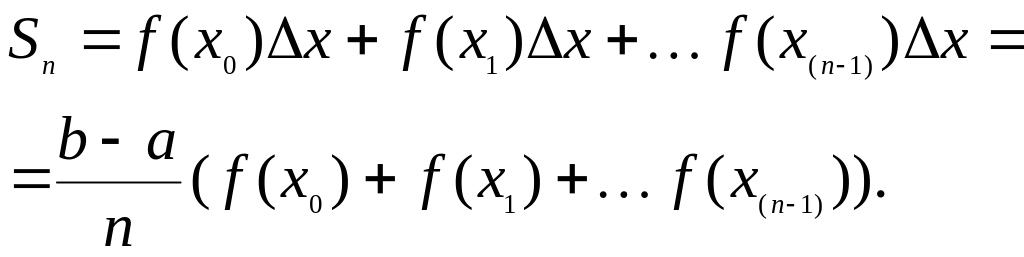
оскільки є довжиною кожного з відрізків розбиття.

Якщо , то , і внаслідок неперервності функції східчаста фігура дедалі менше відрізнятиметься від криволінійної трапеції.

2. Означення визначеного інтеграла та його геометричний зміст.

Нехай функція задана на відрізку . Розіб'ємо цей відрізок на рівних частин точками

У кожному проміжку довжиною оберемо довільну точку і обчислимо відповідне значення функції .

Побудуємо суму яку називають інтегральною сумою для функції на відрізку .

Означення 1. Якщо існує скінченна границя інтегральної суми при , незалежна від способу поділу відрізка на частини та вибору точок , то ця границя називається визначеним інтегралом від функції на відрізку і позначається

Математично це означення можна записати так:

(4)

Відмітимо, що числа та називають нижньою та верхньою межами інтегрування, відповідно.

Згідно з цим означенням рівності (1), (2), (3) тепер можна за­писати у вигляді

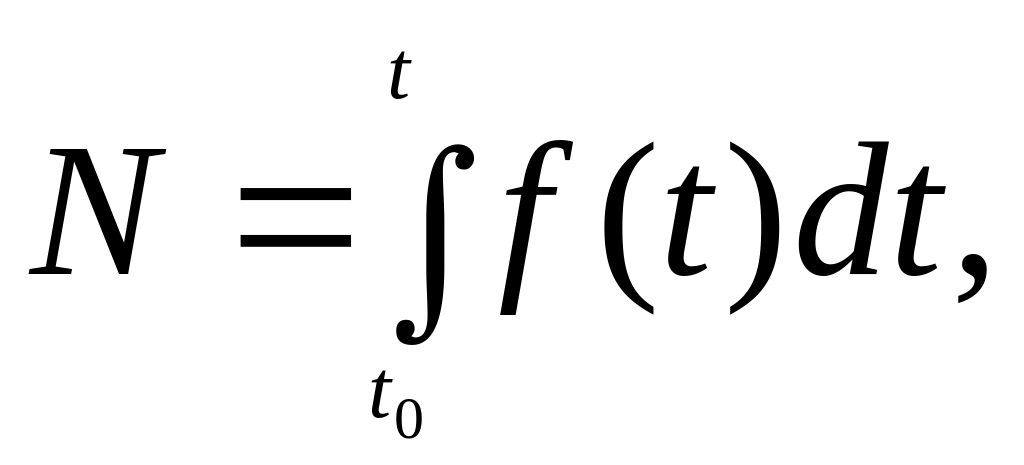, (5)

Перевірка існування скінченної границі інтегральної суми для кожної функції складна. Але такої перевірки робити не треба тому, що використовують таку відому теорему.

Доцільно пояснити геометричний зміст інтеграла: це площа криволінійної трапеції, обмеженої графіком функції , відрізком осі і прямими , , тобто

.