
- •Электромагнетизм
- •Электричество
- •Электрическое поле в вакууме Электрический заряд
- •Электрическое поле
- •Изображение эп
- •Поток вектора
- •Теорема Гаусса
- •Применение теоремы Гаусса
- •Бесконечная плоскость, равномерно заряженная
- •Оператор «набла»
- •Теорема о циркуляции вектора
- •Потенциал
- •Потенциал поля точечного заряда
- •Потенциал поля системы зарядов
- •Момент сил, действующий на диполь
- •Энергия диполя в поле
- •Электрическое поле в веществе
- •Электрическое поле в проводнике
- •Силы, действующие на поверхность проводника
- •Замкнутая проводящая оболочка
- •Электроемкость уединенного проводника
- •Конденсатор
- •Емкость плоского конденсатора
- •Поляризация
- •Связанные заряды в диэлектрике
- •Поляризованость
- •Связь и
- •Теорема Гаусса для
- •Вектор . Теорема Гаусса для
- •Связь между и
- •Условия на границе
- •Преломление линий
- •Связанный заряд у поверхности проводника
- •Поле в однородном диэлектрике
- •Энергия электрического поля Энергетический подход к взаимодействию
- •Уравнение непрерывности
- •З акон Ома для неоднородного участка цепи
- •Применение правил Кирхгофа
- •Закон Джоуля-Ленца
- •Однородный участок цепи
- •Неоднородный участок цепи
- •Магнетизм
- •Сила Лоренца
- •Магнитное поле равномерно движущегося заряда
- •Закон Био-Савара
- •Теорема Гаусса для
- •Сила Ампера
- •Сила, действующая на контур с током
- •Момент сил, действующих на контур с током
- •Работа при перемещении контура с током
- •Магнитное поле в веществе
- •Намагниченность
- •Ток намагничивания
- •Циркуляция вектора
- •Вектор . Теорема о циркуляции
- •Связь и
- •Связь и
- •Граничные условия для и
- •Поле в однородном магнетике
- •Ферромагнетики
- •Относительный характер электрических и магнитных полей
- •Переход от одной исо к другой
- •Релятивистская природа магнетизма
- •Инварианты эмп
- •Электромагнитная индукция
- •Закон электромагнитной индукции
- •Природа электромагнитной индукции
- •Индуктивность
- •Самоиндукция
- •В заимная индуктивность
- •Взаимная индукция
- •Энергия магнитного поля
- •Уравнения Максвелла. Энергия эмп. Ток смещения
- •Система уравнений Максвелла
- •Уравнения Максвелла в дифференциальной форме
- •Теорема Пойнтинга
- •Электрические колебания
- •Свободные колебания
- •Затухающие колебания
- •Величины, характеризующие затухание
- •Вынужденные электрические колебания
- •Резонансные кривые
- •Переменный ток
- •Мощность в цепи переменного тока
Условия на границе
Р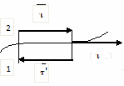 ассмотрим
границу между двумя однородными
изотропными диэлектриками, на которой
есть поверхностный сторонний заряд.
ассмотрим
границу между двумя однородными
изотропными диэлектриками, на которой
есть поверхностный сторонний заряд.
Для вектора
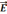 .
.
Пусть  и
и  - напряженности поля у границы в 1 и 2 .
Из
- напряженности поля у границы в 1 и 2 .
Из 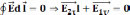
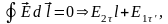 l=0
или
l=0
или 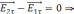
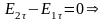
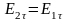
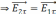 ,
т.е. на границе
раздела тангенциальная составляющая
вектора
,
т.е. на границе
раздела тангенциальная составляющая
вектора
скачка не претерпевает.
Для
вектора 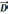 :
:
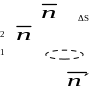 Из
Из 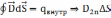 +
+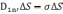 или
или 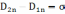 , где
, где 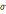 -поверхностная плотность сторонних
зарядов на
границе раздела. Значит , на
границе
раздела
нормальная составляющая вектора
претерпевает скачок.
-поверхностная плотность сторонних
зарядов на
границе раздела. Значит , на
границе
раздела
нормальная составляющая вектора
претерпевает скачок.
Если
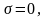 то
то
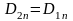 Þ
Þ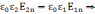
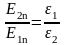
Из
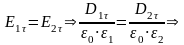
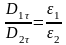 .
.
Итак:
если на границе раздела двух однородных
изотропных диэлектриков сторонних
зарядов нет, то при её переходе 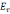 и
и 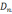 не изменяются,
и
не изменяются,
и 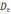 -изменяются.
-изменяются.
Преломление линий
Пусть
на границе раздела диэлектриков 1 и 2
(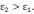 )сторонних зарядов нет .
)сторонних зарядов нет .
Из
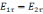 ;
; 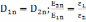 ;
;
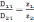 можно видеть ,что ход линий
можно видеть ,что ход линий 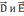
претерпевает
излом , причем чем меньше 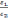 ,
тем
больше отклонение
от нормали к границе раздела.
,
тем
больше отклонение
от нормали к границе раздела.
Условие на границе проводник-диэлектрик
Пусть
проводник 1 граничит с диэлектриком
2 . Из 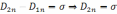 (в проводнике
=0,
(в проводнике
=0,
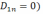 или
или
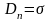 .
.
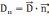 где
где 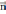 - внешняя по отношению к проводнику
нормаль.
- внешняя по отношению к проводнику
нормаль.
Связанный заряд у поверхности проводника
Установлено
, что если проводник несёт заряд
поверхностной плотности
и граничит с диэлектриком, то в результате
поляризации в диэлектрике у границы
появляется связанный заряд
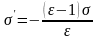 , т.е.
, т.е.
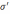 связан с
связан с 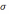 и
имеет противоположный знак.
и
имеет противоположный знак.
Поле в однородном диэлектрике
Рассмотрим
проводник в вакууме , несущий
поверхностный заряд плотности 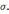 Внутри проводника
=0
, в вакууме он создаёт поле
Внутри проводника
=0
, в вакууме он создаёт поле 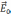 . Заполним всё пространство , где есть
однородным диэлектриком. У границы
с проводником появится связанный
заряд плотности
.
от этого не изменится
. Заполним всё пространство , где есть
однородным диэлектриком. У границы
с проводником появится связанный
заряд плотности
.
от этого не изменится 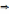 картина
останется прежней.
картина
останется прежней.
По
теореме Гаусса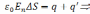
 ,
, 
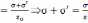 , т.е. заряд
на границе уменьшился в
, т.е. заряд
на границе уменьшился в 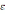 раз.
раз.
Значит
, поле
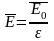 .
.
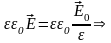
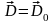
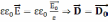 ,
т.е. поле
,
т.е. поле
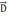 не изменилось.
не изменилось.
Для конденсатора:
1)
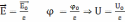
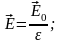
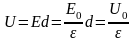 ;
2)
;
2)
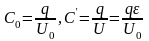
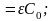
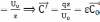
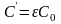 .
.
Энергия электрического поля Энергетический подход к взаимодействию
1) Пусть точечные
заряды 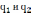 в некоторой K
–системе совершили перемещения
в некоторой K
–системе совершили перемещения
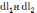 При этом
При этом 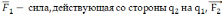 -
со стороны
-
со стороны
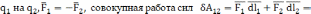
=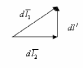
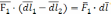 ;
;
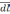 - перемещение
- перемещение 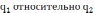 .
.
Из 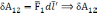 не зависит
от системы отсчета.
не зависит
от системы отсчета.
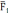 - консервативная
- консервативная 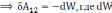 =
=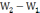 приращение
приращение
потенциальной
энергии 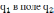 .
W
зависит только от расстояния между
зарядами.
.
W
зависит только от расстояния между
зарядами.
2)Для трех зарядов : работа всех сил взаимодействия
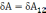 +
+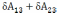 . Для каждой пары
. Для каждой пары
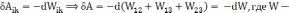 энергия взаимодействия данной системы
зарядов ( зависит от конфигурации
системы ).
энергия взаимодействия данной системы
зарядов ( зависит от конфигурации
системы ).
Аналогично для любого числа зарядов
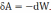
Энергия взаимодействия
Для трех
зарядов энергия взаимодействия
W=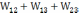
W=
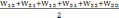 =
= 
или 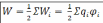
Полная энергия взаимодействия
Для непрерывного
объемного распределения зарядов
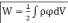 , где
, где  - потенциал, создаваемый всеми зарядами
системы в элементе объема dV.
Аналогично для поверхностного
распределения заряда
- потенциал, создаваемый всеми зарядами
системы в элементе объема dV.
Аналогично для поверхностного
распределения заряда 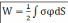 , где
- потенциал, создаваемый всеми зарядами
системы в элементе площади dS.
, где
- потенциал, создаваемый всеми зарядами
системы в элементе площади dS.
Энергия уединенного проводника
Для проводника
j=const;
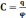 ;
W
;
W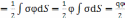 .
Тогда
.
Тогда 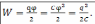 .
.
Энергия конденсатора
Для
конденсатора 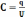 ;
; 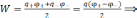
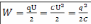 .
.
Энергия электрического поля
Энергия поля плоского конденсатора:
W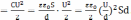 В однородном диэлектрике
В однородном диэлектрике 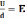 и
и
 , где V
– объем поля.
, где V
– объем поля.
Объемная плотность
энергии поля  .
.
Постоянный электрический ток
Электрический ток – направленное движение зарядов под действием
электрического поля.
Сила тока ( I ) – заряд , переносимый полем в единицу времени.
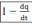
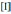 = 1 А – ампер.
= 1 А – ампер.
Плотность тока ( j ) - векторная физическая величина , численно равная
отношению тока dI, проходящего нормально сквозь элементарную площадку к ее
площади
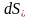

Направление
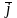 совпадает с направлением движения
«+» зарядов.
совпадает с направлением движения
«+» зарядов.Если ток создают носители обоих знаков, то
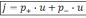
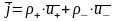 ,
где
,
где
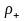 и
и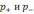
 -
объемные
-
объемные
плотности «+»
и «-» зарядов; 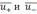 - скорости дрейфа (упорядоченного
движения) «+»
- скорости дрейфа (упорядоченного
движения) «+»
и «-» зарядов .
В металле
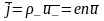 ,
где e
– заряд электрона, n
– концентрация свободных
электронов.
,
где e
– заряд электрона, n
– концентрация свободных
электронов.Поле графически изображают аналогично полю
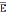 .
.Сила тока через поверхность
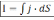
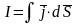 ,
т.е I
– величина алгебраическая и зависит
от выбора нормали к dS.
,
т.е I
– величина алгебраическая и зависит
от выбора нормали к dS.
