Изображение эп

ЭП условно изображают в виде линий напряженности (ЛН), причем:

1. В каждой точке ЛН вектор направлен по касательной.

2. Плотность ЛН (число линий, проходящих через единицу площади нормально расположенной поверхности) полагают равной │ │ в данной точке.

3. ЛН приписывают направление в сторону направления .

4. По картине ЛН можно определить в любой точке поля.

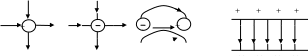
Поток вектора

Пусть напряженность поля в некоторой области пространства равна . Тогда количество линий , проходящих через элементарную площадку dS будет:

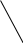
α

α

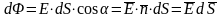, где 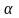- угол между и ,

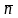- орт нормали к dS.

dS

Поток вектора через поверхность (Ф) – количество силовых линий поля вектора,

проходящих сквозь данную поверхность.

Тогда поток вектора сквозь произвольную поверхность S:

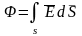
Поток Ф:

1. величина алгебраическая, зависит от конфигурации поля и от направления ;

2. для замкнутых поверхностей принято брать нормаль ,направленный наружу области, охватываемой данной поверхностью.

Теорема Гаусса

Теорема Гаусса: поток вектора напряженности через замкнутую поверхность равен

алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на : .

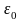Доказательство: окружим точечный заряд q замкнутой поверхностью S и найдем поток вектора через элемент площади :

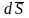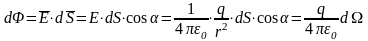
где 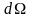- телесный угол с вершиной в точке q, опирающийся на dS.

Тогда 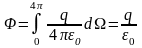или

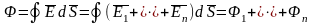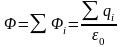Для поля нескольких зарядов: или , где 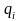- заряды , заключенные внутри данной поверхности.

• Е сли q=0 (вне поверхности), то Ф=0 : для части поверхности, сквозь которую поток входит в область V , для части, сквозь которую выходит 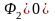. Угол 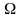для обоих потоков одинаков, их величины равны 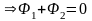или: сколько линий вошло в область V, столько же из нее и вышло.

• Поле и поток Ф зависят от конфигурации

системы зарядов внутри замкнутой поверхности,

однако значение потока от нее не зависит.

Применение теоремы Гаусса

Теорема Гаусса эффективна при расчете симметричных полей.

Бесконечная плоскость, равномерно заряженная

с плотностью +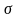

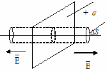Поле симметрично относительно плоскости. Вырежем

цилиндр нормально к плоскости с площадью основания ΔS. Тогда

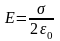
• Поле однородно E=const.

• Е 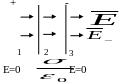сли 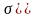, то направлен к плоскости.

Две бесконечные плоскости, равномерно

заряженные с плотностями + и -

Из предыдущего и с учетом следует, что в областях 1 и 3 Е=0, в области 2 .

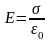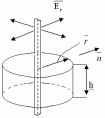
Бесконечно длинная нить, равномерно заряженная

с линейной плотностью +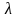

Поле осесимметрично, поток – только через

боковую поверхность .На расстоянии r от нити

значение напряженности поля E_{r .} Тогда

.

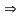
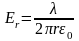• Если 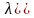, то E_r направлено к нити.

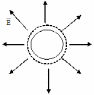Сферическая поверхность радиуса а, равномерно

заряженная зарядом +q

Поле центральносимметричное;

Для r ≥ а

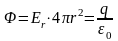
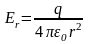
• Для r a q=0

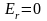
• Для q = -|q| E_r направлен к центру сферы.

Шар радиуса а, равномерно заряженный зарядом +q

Поле центральносимметричное, для r ≥ a (cм. выше).

Д ля : ; .

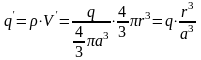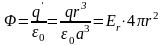
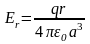Теорема Гаусса в дифференциальной форме

Пусть заряд q распределен по объему V со средней плотностью 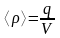и поверхность

S заключает в себе объем V. Тогда или 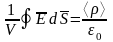. Устремим V к некоторой его точке: . При этом и .

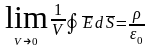Величина - дивергенция поля Е.

Тогда 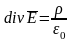- теорема Гаусса в дифференциальной форме: дивергенция поля вектора 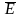в данной точке поля зависит только от плотности 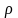электрического заряда в этой точке.

Замечания:

1) - скалярная функция точки, т.е. зависит от координат (и от системы

координат).

2) из математики известно, что в декартовой системе координат

, т.е. теорема Гаусса устанавливает связь между 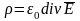и изменением в окрестностях точки ( );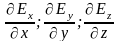

3) во всех точках поля точечного заряда, кроме точки нахождения заряда,

сумма 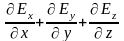одинакова и равна нулю, т.к. в них .

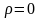4) в точках поля, где находятся источники поля («+»заряды). Линии

напряженности поля в них начинаются;

в точках поля где находятся стоки поля ( «-» заряды ). Линии

напряженности поля в них оканчиваются.