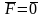- •Электромагнетизм
- •Электричество
- •Электрическое поле в вакууме Электрический заряд
- •Электрическое поле
- •Изображение эп
- •Поток вектора
- •Теорема Гаусса
- •Применение теоремы Гаусса
- •Бесконечная плоскость, равномерно заряженная
- •Оператор «набла»
- •Теорема о циркуляции вектора
- •Потенциал
- •Потенциал поля точечного заряда
- •Потенциал поля системы зарядов
- •Момент сил, действующий на диполь
- •Энергия диполя в поле
- •Электрическое поле в веществе
- •Электрическое поле в проводнике
- •Силы, действующие на поверхность проводника
- •Замкнутая проводящая оболочка
- •Электроемкость уединенного проводника
- •Конденсатор
- •Емкость плоского конденсатора
- •Поляризация
- •Связанные заряды в диэлектрике
- •Поляризованость
- •Связь и
- •Теорема Гаусса для
- •Вектор . Теорема Гаусса для
- •Связь между и
- •Условия на границе
- •Преломление линий
- •Связанный заряд у поверхности проводника
- •Поле в однородном диэлектрике
- •Энергия электрического поля Энергетический подход к взаимодействию
- •Уравнение непрерывности
- •З акон Ома для неоднородного участка цепи
- •Применение правил Кирхгофа
- •Закон Джоуля-Ленца
- •Однородный участок цепи
- •Неоднородный участок цепи
- •Магнетизм
- •Сила Лоренца
- •Магнитное поле равномерно движущегося заряда
- •Закон Био-Савара
- •Теорема Гаусса для
- •Сила Ампера
- •Сила, действующая на контур с током
- •Момент сил, действующих на контур с током
- •Работа при перемещении контура с током
- •Магнитное поле в веществе
- •Намагниченность
- •Ток намагничивания
- •Циркуляция вектора
- •Вектор . Теорема о циркуляции
- •Связь и
- •Связь и
- •Граничные условия для и
- •Поле в однородном магнетике
- •Ферромагнетики
- •Относительный характер электрических и магнитных полей
- •Переход от одной исо к другой
- •Релятивистская природа магнетизма
- •Инварианты эмп
- •Электромагнитная индукция
- •Закон электромагнитной индукции
- •Природа электромагнитной индукции
- •Индуктивность
- •Самоиндукция
- •В заимная индуктивность
- •Взаимная индукция
- •Энергия магнитного поля
- •Уравнения Максвелла. Энергия эмп. Ток смещения
- •Система уравнений Максвелла
- •Уравнения Максвелла в дифференциальной форме
- •Теорема Пойнтинга
- •Электрические колебания
- •Свободные колебания
- •Затухающие колебания
- •Величины, характеризующие затухание
- •Вынужденные электрические колебания
- •Резонансные кривые
- •Переменный ток
- •Мощность в цепи переменного тока
Оператор «набла»
Для упрощения
расчетов введен векторный дифференциальный
оператор
 (набла). В декартовой системе координат
(набла). В декартовой системе координат
 ,
где
,
где
 - орты X,
Y,
Z.
- орты X,
Y,
Z.


не имеет смысла сам по себе, а только при символическом умножении его на некоторую величину (векторную или скалярную).
Теорема о циркуляции вектора
Известно, что поле
центральных сил консервативно,
т.е.
 .
Электростатическое поле системы точечных
зарядов –поле центральных сил, т.е. оно
консервативно.
.
Электростатическое поле системы точечных
зарядов –поле центральных сил, т.е. оно
консервативно.
Тогда из
 и
и

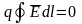 или
или
 - теорема
о циркуляции
вектора
:
циркуляция вектора Е по замкнутому
контуру равна нулю.
- теорема
о циркуляции
вектора
:
циркуляция вектора Е по замкнутому
контуру равна нулю.
Потенциал
Известно, что
работа консервативных сил при перемещении
частицы из т.1 в т.2 поля:
 , где
, где
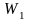 и
и
 - значения потенциальной энергии частицы
в точках 1 и 2,
- значения потенциальной энергии частицы
в точках 1 и 2,
 -
сила ,
-
сила ,
 -
элементарное
перемещение. Тогда для электрического
поля
-
элементарное
перемещение. Тогда для электрического
поля
 ,
где
,
где
 и
и
 -
потенциалы
поля в т.1 и т.2.
-
потенциалы
поля в т.1 и т.2.
Потенциал ( )
– скалярная
физическая величина,
численно
равная потенциальной
)
– скалярная
физическая величина,
численно
равная потенциальной
энергии единичного положительного точечного заряда в данной точке поля.
 =1В
– вольт.
=1В
– вольт.
определяется с точностью до произвольной аддитивной постоянной, т.е.
произвольной
точке О можно присвоить любое значение
 ,
а потенциалы всех других
,
а потенциалы всех других
точек поля однозначно определятся относительно т.О.
Все электрические явления определяются не значением в какой-либо точке, а
разностью потенциалов в избранных точках поля.
Потенциал поля точечного заряда
Для
дифференциально малых
 из
из

 ,
где
,
где
 -
-
дифференциально малое приращение на .
Значит, зная
 ,
можно определить
(с точностью до
C=const).
,
можно определить
(с точностью до
C=const).
Для поля точечного заряда:
 ,
где
,
где
 ,
С=const.
,
С=const.
Полагаем, что
при

 принимаем
С=0.
Тогда
принимаем
С=0.
Тогда
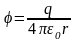 .
.
Потенциал поля системы зарядов
Для системы неподвижных точечных зарядов:
 ,
где
,
где
 - принцип
суперпозиции
- принцип
суперпозиции
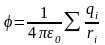 .
Если заряд распределен
непрерывно:
.
Если заряд распределен
непрерывно:
а) по объему:
 ,
где
-
объемная плотность
заряда в объеме
,
где
-
объемная плотность
заряда в объеме
 .
.
б) по
поверхности:
 ,
где
,
где
 поверхностная
плотность заряда на
поверхностная
плотность заряда на
площади dS.
Связь и
Пусть
перемещение
направлено
вдоль оси
Х. Тогда
 ,
где
,
где
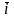 -
орт оси Х ,
-
орт оси Х ,
dx – приращение координаты х.
 ,
где
,
где
 - проекция
на
- проекция
на


или
 , т.е.
, т.е.
 надо дифференцировать только по х ,
считая y
и z
надо дифференцировать только по х ,
считая y
и z
постоянными.
Аналогично
 ;
;
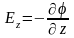

Таким образом,
зная
 ,всегда можно восстановить
,всегда можно восстановить
 .
.
Связав систему
координат с ортом касательной к l
, получим:

и
 , т.е. проекция
на
равна минус производной потенциала
по
, т.е. проекция
на
равна минус производной потенциала
по
направлению .
Эквипотенциальные поверхности
Эквипотенциальная поверхность – поверхность, все точки которой имеют
одинаковый потенциал.
Из
и
 что проекция
на касательную
к эквипотенциальной поверхности равна
нулю, т.е.
нормален
к эквипотенциальной поверхности.
что проекция
на касательную
к эквипотенциальной поверхности равна
нулю, т.е.
нормален
к эквипотенциальной поверхности.
Рассмотрим по нормали к эквипотенциальной поверхности в сторону уменьшения .
Т огда
огда
 <0
и
>0
, т.е.
направлен
нормально к эквипотенциальной
поверхности
в сторону уменьшения потенциала.
<0
и
>0
, т.е.
направлен
нормально к эквипотенциальной
поверхности
в сторону уменьшения потенциала.
Эквипотенциальные поверхности (эквипотенциали ) удобно проводить с одинаковой
 между ними. Тогда по их густоте можно
судить о напряженности поля (где
плотность эквипотенциалей больше, там
напряженность выше).
между ними. Тогда по их густоте можно
судить о напряженности поля (где
плотность эквипотенциалей больше, там
напряженность выше).
Электрический диполь
Электрический диполь – система из двух одинаковых по модулю разноименных
зарядов,
находящихся на расстоянии
 друг от друга.
друг от друга.
 Поле
диполя:
Поле
диполя:
р
A
ассматривают на расстоянии r>>осесимметрично.
Для т. А :


 ,
,
 .
.
Тогда
 или
или
 , где
, где
 -
дипольный
электрический момент (или
дипольный момент).
-
дипольный
электрический момент (или
дипольный момент).
для
 :
:
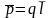 ,
где q>0.
,
где q>0.
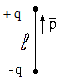 По известному
φ(r)
определим
.
Для этого найдем
По известному
φ(r)
определим
.
Для этого найдем
 .
.
Из



 , тогда
, тогда


Для
 :
:
 . Для
. Для
 :
:
 , т.е.
, т.е.


Сила, действующая на диполь
Поместим
диполь в неоднородное поле. На него
действует сила
 .
.
 -
приращение Е на отрезке
в направлении
.
-
приращение Е на отрезке
в направлении
.
мало
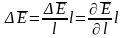 или
или
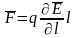 или
или

 .
.
В однородном поле
 , т.е к диполю приложена равнодействующая
, т.е к диполю приложена равнодействующая