Метод деления пополам (метод вилки)
полагаем x0 = = 0 , 0 = , 0 = | – |, причём f(0)·f(0) < 0;
пусть уже известны xn , n , n , n , где f(n)·f(n) 0;
если n и |f(xn)| , то процесс завершён, xn – приближённое значение корня;
если n > или |f(xn)| > , то xn+1 =
– середина отрезка [n
; n],
[n+1
; n+1]
=
,
n+1
=
,
возврат к шагу 2.
Применение метода иллюстрируют следующие рисунки:
Т
еорема
(о методе деления пополам).
Пусть известен отрезок [;
],
в котором есть ровно один корень
уравнения f(x)
= 0, причём f()·f()
< 0. Метод деления пополам определяет
последовательность {xn}n
N
, сходящуюся к корню r
[;
]
со скоростью геометрической прогрессии.
Доказательство.
Для обоснования сходимости
нужно повторить доказательство теоремы
о существовании корня непрерывной
функции.
Во-первых, описанный алгоритм всегда определяет новое приближение xn+1 по уже известным. Действительно, это следует из того, что одно из условий f(n)·f(xn+1) < 0 или f(xn+1)·f(n) < 0, используемых для вычисления n+1 , n+1 в шаге 4 описанного алгоритма, обязательно будет выполнено: если это не так, то обе эти величины положительны (в случае обращения в ноль одной из них корень уже найден), а значит, f(n)·f(xn+1)2·f(n) > 0, т.е. f(n)·f(n) > 0, вопреки пункту 2 алгоритма.
Далее, в ходе итерационного процесса на самом деле строится последовательность вложенных отрезков [0 ; 0] = [x0 ; x1] [1 ; 1] … , на концах которых функция f(x) принимает значения противоположных знаков: f(i)·f(i) < 0. Формально,
[i+1
; i+1]
=
.
Эта последовательность
вложенных отрезков стягивающаяся, т.к.
из построения i+1
= |i+1
– i+1
| =
.
Значит, все эти отрезки содержат общую
точку ,
причём
, f()2
=
0, т.е. f()
= 0, и значит,
= r
– корень
функции f(x),
к которому сходятся концы рассматриваемых
стягивающихся отрезков – члены
последовательности {xn}n
N
.
Утверждение о
скорости сходимости следует из очевидной
оценки |xi+1
– r|
i+1
=
.
Теорема доказана.
Примеры: 1. Уточнить значение корня функции f(x) = ln x на отрезке [0,5; 1,7] с точностью = 0,05. Точное значение корня, очевидно, равно 1.
Таким образом, приближённым значением корня будет 0,99, поскольку 5 = 0,038 < 0,05 и |f(x5)| = 0,0126 < 0,05.
2. Уточнить значение корня функции f(x) = 32·x3 – 48·x2 + 22·x – 3 на отрезке [0; 0,34] с точностью = 0,01. Точное значение корня 0,25.
Поскольку 6 = 0,005 < 0,01 и |f(x6)| = 0,0013 < 0,01, заключаем, что приближённое значение корня равно x6 0,25.
В методе деления
пополам можно контролировать количество
итераций: если
– заданная
погрешность, то из соотношения k
=
находим количество требуемых итераций:
.
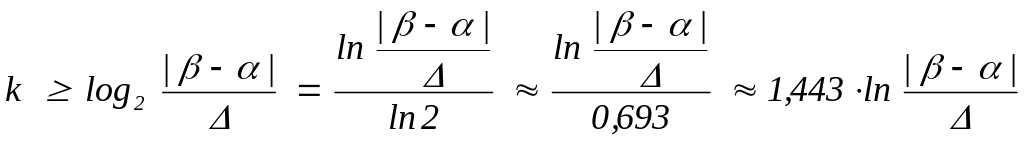Так, для первого
из рассмотренных выше примеров сразу
можно оценить k
1,443·ln
= 1,443·ln
(20·1,2)
4,59, т.е. k
= 5. Для
второго примера k
1,443·ln
= 1,443·ln
(50)
5,65, т.е. k
= 6.
Рассмотрим теперь вопрос о порядке сходимости метода деления пополам. Во многих книгах (в том числе, к сожалению, и в учебнике [7, стр. 90]) утверждается, что это метод первого порядка. Однако такое заключение необоснованно: следующий пример иллюстрирует ошибочность этого вывода.
Пример. Уточнить корень на отрезке [0; 1] с точностью до = 0,001. Точное значение корня r = 0,49804687499.
В таблицах ниже приведены вычисления по методу деления пополам. Следует учесть, что значения f(xi) в методе деления пополам сами по себе не важны, метод деления пополам оперирует лишь знаками этих значений, которые полностью определяются знаками разности xi – r. Поэтому в приводимых ниже вычислениях участвуют не значения функции (которая даже не задана), а знаки этих значений.
Представленные в таблицах отношения i+1 / i показывают, что подобрать константу c со свойством |xi+1 – r| c·|xi – r| при всех достаточно больших i N не представляется возможным. Причина состоит в непредсказуемом поведении величины i+1 / i при “переходе через корень”. Таким образом, метод деления пополам достаточно быстро сходится (со скоростью геометрической прогрессии), но утверждать, что он имеет первый порядок сходимости, нельзя.
Краткая характеристика метода деления пополам приведена в приложении (таблица I).