§ 3. Метод наименьших квадратов

Как правило, табличные значения функций задаются не точно, а приближённо. Поэтому попытки провести через эти точки график многочлена зачастую не приближают к исходной функции, а даже удаляют от неё, т.к. погрешности исходных значений приведут к “разбалтыванию” графика многочлена.

Можно поставить задачу иначе: в классе функций определённого вида найти функцию, наименее уклоняющуюся в заданных точках от заданных значений. Более точно, по заданной таблице

x1	x2	…	xn–1	xn
y1 = f(x1)	y2 = f(x2)	…	yn–1 = f(xn–1)	yn = f(xn)

требуется в заданном классе функций Ф найти функцию , для которой минимально среди всех функций   Ф.

Как правило, класс функций Ф является параметрическим семейством дифференцируемых функций: Ф = {(x, a₁ , … , a_m) | (a₁ ; … ; a_m)  }, где  – некоторое открытое множество в пространстве R ^m. Поэтому требуется найти значения параметров a₁ , … , a_m , для которых достигается минимум величины . Эта задача на экстремум приводит к необходимым условиям равенства нулю всех частных производных рассматриваемой минимизируемой функции U:

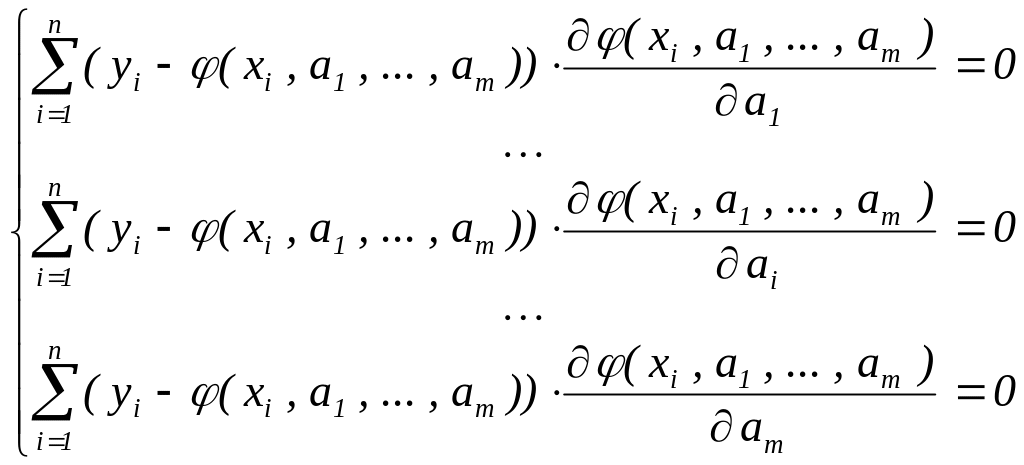
В случае m = n и дважды непрерывно дифференцируемой функции  можно сформулировать и достаточные условия минимума, которые состоят в неотрицательности всех собственных чисел симметричной матрицы вторых производных

В частности, это верно, если матрица вторых производных положительно определена. По критерию Сильвестра это равносильно положительности всех главных миноров этой матрицы:

.

Наиболее часто используются следующие двухпараметрические семейства функций:

(x, a, b) = ax + b, (x, a, b) = a + bln x,

(x, a, b) = ax^b, (x, a, b) = ae^bx,

(x, a, b) = a + , (x, a, b) = , (x, a, b) = .

Используются и трёхпараметрические семейства:

(x, a, b) = ax² + bx + c, (x, a, b) = ax^b + c,

(x, a, b) = ae^bx + c, (x, a, b) = a10^bx + c .

Пример: 1. Рассмотрим приближение линейной функцией по методу наименьших квадратов.

Здесь (x, a, b) = ax + b, , и для определения параметров a, b в соответствии с изложенной выше общей теории получается система линейных уравнений:

где .

Полученная система двух линейных уравнений с двумя неизвестными имеет единственное решение тогда и только тогда, когда её определитель не равен нулю: . При n > 1 и попарно различных узлах x_i (1  i  n) это ограничение выполнено:

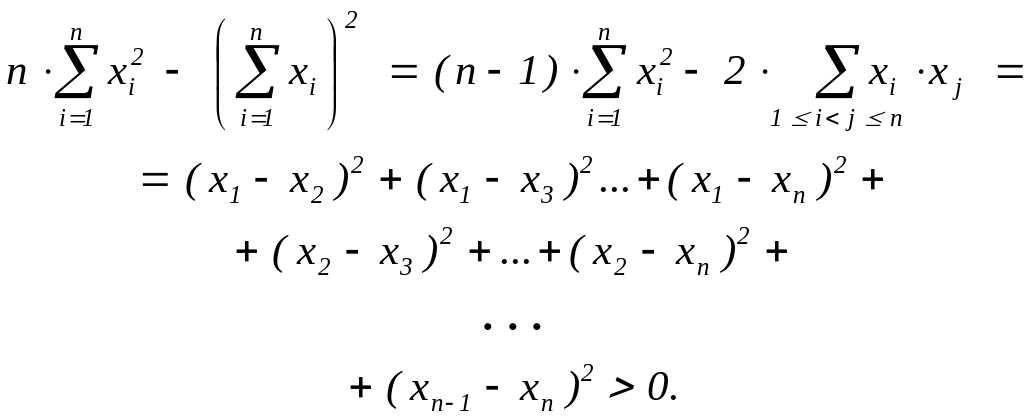
Поэтому рассматриваемая линейная система имеет единственное решение при n > 1. Нетрудно понять, что её решения – параметры a и b – действительно доставляют минимум квадратичного отклонения . В самом деле,

,

и , т.е. матрица вторых частных производных положительно определена.

2. Для приближения квадратичной функцией (x, a, b) = ax² +bx + c аналогичные вычисления приводят к системе линейных уравнений

,

где (0  k  4, 0  m  1).

Рассмотренные выше линейные и квадратичные приближения являются основными. Приведённые выше другие виды приближающих функций приводят к системам нелинейных уравнений. Чтобы избежать решения таких систем, можно сводить эти задачи к более простым приближениям.

Примеры: 1. Степенные приближения (x, a, b) = ax^b сводятся к линейным: если a > 0 и x > 0, то, прологарифмировав (x, a, b), получим функцию F(ln x, ln a, b) = ln (x, a, b) = ln a + bln x . Таким образом, можно “прологарифмировать” исходную таблицу и найти линейное приближение к полученной функции.

x1	…	xn		ln x1	…	ln xn
y1	…	yn		ln y1	…	ln yn

Если найдена приближающая функция F(z, u, v) = u + vz для полученной таблицы, то параметры a = e^u , b = v приведут к приближающей функции ax^b для исходной таблицы.

2. Аналогично для (x, a, b) = ae^bx после логарифмирования получим линейное приближение F(x, ln a, b) = bx + ln a .

3. Для приближения дробно-линейной функцией (x, a, b) = достаточно рассмотреть функцию F(x, a, b) = = ax + b. Таким образом, можно “обратить” исходную таблицу и найти линейное приближение к полученной функции.

x1	…	xn		x1	…	xn
y1	…	yn			…

Если найдена приближающая функция F(x, a, b) = ax + b для полученной таблицы, то параметры a и b приведут к приближающей функции (x, a, b) = для исходной таблицы.

4. Приближение семейством функций вида (x, a, b) = сводится к предыдущей задаче: F(x, a, b) = .

1. Пример: По заданной таблице значений с помощью метода наименьших квадратов

а) найти приближающую линейную функцию f(x, a, b) = ax + b;

б) найти приближающую квадратичную функцию

f(x, a, b, c) = ax² + bx + c;

в) для каждой из найденных функций вычислить сумму квадратов отклонений

и сравнить качество полученных приближений.

y	2,93	6,10	9,44	8,25	9,79	–6,03	7,67	4,38	4,40	7,05
x0	4,33	2,72	6,02	7,03	9,90	5,67	2,29	5,43	1,14	–7,41

а) Находим линейную приближающую функцию (x, a, b) = ax + b по методу наименьших квадратов. Для этого минимизируем сумму квадратов отклонений

Условие минимума:

,

где .

Вычисляем коэффициенты системы и решаем её методом Гаусса:

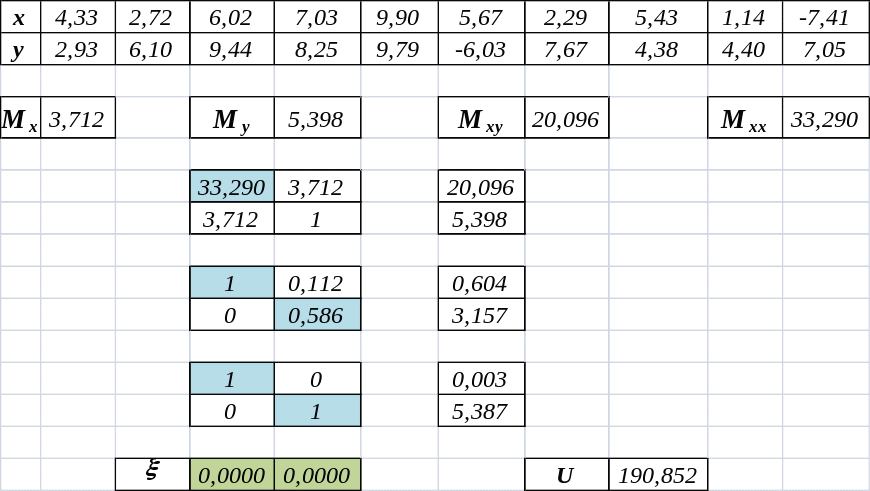
Итак, a  0,0030, b  5,3869, (x, a, b)  0,003x + 5,387, U  190,852.

б) Решаем аналогично предыдущему. Будем искать линейную приближающую функцию f(x, a, b) = ax² + bx + c по методу наименьших квадратов. Для этого минимизируем сумму квадратов отклонений

Условие минимума:

,

где .

Вычисляем коэффициенты системы и решаем её методом Гаусса:

Таким образом, для a  0,054, b  –0,094, с  3,944, найдена приближающая функция (x, a, b)  0,054x² – 0,094x + 3,944, U  170,282.

Видно, что квадратичное отклонение квадратичного приближения меньше, нежели квадратичное отклонение линейного приближения. Квадратичное приближение в данном случае лучше линейного.

Ещё одно применение метода наименьших квадратов связано со следующей задачей, часто возникающей на практике:

Нужно найти значения n различных величин x₁ , … , x_n , которые нельзя измерить непосредственно, но известно, что они связаны линейными зависимостями, коэффициенты которых определяются в ходе m измерений.

Таким образом, речь идёт о решении системы m линейных уравнений с n неизвестными

.

Для того чтобы величины x₁ , … , x_n можно было найти однозначно, должно быть выполнено ограничение m  n (при m < n система имеет бесконечное число решений). Кроме того, будем предполагать, что ранг основной матрицы системы равен n – количеству неизвестных (критерий определённости системы).

Поскольку из-за погрешностей измерений и вычислений величин a_ij и b_i (1  i  m, 1  j  n) может получиться несовместная система линейных уравнений, разумно не решать полученную систему, а искать величины x₁ , … , x_n , для которых отклонение будет минимально. Эта задача минимизации приводит к необходимым условиям

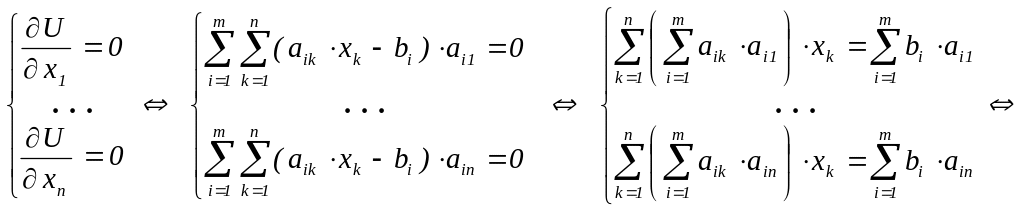
Это система n линейных уравнений с n неизвестными, коэффициенты которой можно интерпретировать как скалярные произведения столбцов a^(s)a^(t) исходной матрицы A = (a_ij).

Поэтому определитель матрицы этой системы

обращается в ноль тогда и только тогда, когда строки его линейно зависимы, т.е. 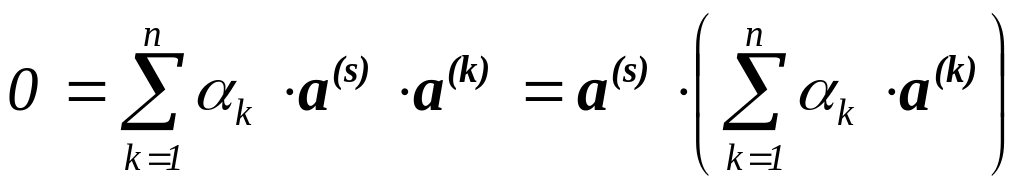(1  s  n). Это возможно только в случае линейной зависимости столбцов матрицы А = (a_ij). Это невозможно ввиду ограничения rg(A) = n.

Таким образом, при сделанных предположениях полученная система линейных уравнений всегда имеет единственное решение. Это решение действительно доставляет минимум минимизируемой функции. Для того, чтобы убедиться в этом, нужно понять, что все собственные числа матрицы вторых производных неотрицательны. Но эта матрица, как не трудно проверить, в рассматриваемом случае равна

.

Поэтому, если 2AA ^tv = v, то 2v ^tAA ^tv = vv ^t и .

Пример. Пусть нужно определить величины x, y, связанные линейными зависимостями , где . Легко видеть, что эта система несовместна.

Для решения задачи по методу наименьших квадратов составляем систему и находим решение . Конечно, это решение не удовлетворяет ни одному из уравнений исходной системы, но при этих значениях вектор разности левой и правой частей системы имеет наименьшую длину. Действительно, матрица вторых производных минимизируемой функции

U(x, y) = (x+2y – 8,5)² + (2x + y – 6,7)² + (x + 3y – 11,1)²

равна и является положительно определённой, так, что в найденной точке достигается минимум функции U(x, y).