
- •Вместо введения: о погрешностях при решении прикладных задач
- •Глава I. Численные методы решения уравнений
- •§ 1. Задача локализации корней
- •Ограничение корней
- •Локализация корней
- •Простейший (грубейший) алгоритм локализации корней:
- •§ 2. Понятие об итерационных методах уточнения корней
- •Метод деления пополам (метод вилки)
- •§ 3. Методы хорд и касательных
- •Метод хорд для монотонных выпукло-вогнутых функций
- •Метод касательных для монотонных выпукло-вогнутых функций
- •§ 4. Метрические и банаховы пространства. Теорема о неподвижной точке
- •Матричные нормы
- •§ 5. Метод простой итерации
- •§ 6. Применение метода простой итерации к решению
- •Условие h([; ]) [; ] :
- •Глава II. Вычисления в линейной алгебре
- •§ 1. Метод Гаусса и его улучшения для повышения точности решения
- •§ 2. Метод простой итерации и метод Зейделя
- •§ 3. Подготовка к применению метода простой итерации
- •§ 4. Проблема собственных значений
- •Глава III. Численное интегрирование
- •§ 1. Метод прямоугольников
- •§ 2. Метод трапеций
- •§ 3. Метод Симпсона (параболическое интерполирование)
- •Глава IV. Некоторые методы аппроксимации функций
- •§ 1. Интерполяционный многочлен Лагранжа
- •§ 2. Интерполяционный многочлен Ньютона
- •§ 3. Метод наименьших квадратов
- •Глава V. Некоторые методы численного решения дифференциальных уравнений
- •Приложение: Сводка характеристик численных методов
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
§ 2. Метод простой итерации и метод Зейделя
Метод простой итерации. Этот метод при определённых условиях применим и к решению систем линейных уравнений, поскольку любую систему A·X = b можно рассматривать как уравнение вида F(X) = X, где F(X) = (In – D·A)·X + D·b с любой невырожденной (nn)-матрицей D, в банаховом пространстве nR. Действительно,
F(X) = X (In – D·A)·X + D·b = X In·X – D·A·X + D·b = X
D·A·X = D·b A·X = b.
Последняя эквивалентность в этой цепочке обусловлена невырожденностью матрицы D.
Для применимости этого метода функция F(X) = (In – D·A)·X + D·b должна быть сжимающим отображением, т.е. удовлетворять условию ||F(X) – F(Y)|| c·||X – Y|| при некотором 0 < c < 1 и любых X, Y nR. Ясно, что F(X) = B·X + e, где B = In – D·A, e = D·b.
Теорема (достаточное условие сходимости метода простой итерации). Пусть для некоторой матричной нормы верно ||B|| < 1. Тогда отображение F(X) = B·X + e будет сжимающим, а значит, метод простой итерации Xn+1 = F(Xn) будет сходиться при любом начальном приближении X0 к единственному решению X уравнения F(X) = X. При этом
||X
– Xn||
![]() , ||Xn+1
– X||
||B||·||Xn
– X||.
, ||Xn+1
– X||
||B||·||Xn
– X||.
Доказательство. Нужно обосновать только сжимаемость отображения F – все остальные утверждения следуют из теоремы о неподвижной точке сжимающего отображения в банаховом пространстве.
Имеем ||F(X)
– F(Y)||
= ||B·(X
– Y)||
||B||·||X
– Y||,
т.е. в качестве коэффициента сжатия
можно взять c
= ||B||
< 1. Если
положить X0
= e,
то X1
= B·e
+ e
, и из доказанная ранее оценка ||X
– Xn||
![]() приводит к
нужному неравенству ||X
– Xn||
приводит к
нужному неравенству ||X
– Xn||
![]() .
.
Теорема доказана.
Пример. Решить систему с точностью до 0,001:
 .
.
 –
–
система в виде X
= B·X
+ e,
где
 ,
и
,
и
||B|| = max{0,4+0,2+0,3+0,05; 0,2+0,2+0,3+0,1;
0,05+0,3+0,5+0,1; 0,5+0,1+0,1+0,1} = 0,95 < 1.
Поэтому применим метод простой итерации:

В этой таблице n = ||Xn – Xn–1|| , а вычисления ведутся пока n – заданной точности вычислений.
Если оценивать
количество итераций по формуле ||X
– Xn||
, то получим
![]() ,
т.е. n+1
<
,
т.е. n+1
<
![]() .
Таким образом, иногда метод сходится
быстрее этой оценки.
.
Таким образом, иногда метод сходится
быстрее этой оценки.
Возникает вопрос: для любой ли матрицы A можно найти такую обратимую матрицу D, что ||B|| = ||In + D·A|| < 1 для некоторой матричной нормы ? Ответ, конечно, утвердителен: например, если взять D = –A–1, то ||B|| = ||0|| = 0 < 1. В некоторых случаях матрицу D найти легко:
Лемма (о матрицах с диагональным преобладанием).
(1) Если матрица
А с диагональным преобладанием по
строкам:
![]() (1
i
n),
то ||In
– D·A||
< 1
для
диагональной
матрицы D
с элементами di
= aii–1
по диагонали. В этом случае итерационный
процесс Xk+1
= (In
– D·A)·Xk
+ e
сходится при любом начальном приближении
X0
к единственному решению системы
уравнений A·X
= b
= D–1·e
.
(1
i
n),
то ||In
– D·A||
< 1
для
диагональной
матрицы D
с элементами di
= aii–1
по диагонали. В этом случае итерационный
процесс Xk+1
= (In
– D·A)·Xk
+ e
сходится при любом начальном приближении
X0
к единственному решению системы
уравнений A·X
= b
= D–1·e
.
(2) Если матрица
А с диагональным преобладанием по
столбцам:
![]() (1
j
n),
то ||In
– A·D||1
< 1
для
диагональной
матрицы D
с элементами di
= aii–1
по диагонали. В этом случае итерационный
процесс Yk+1
= (In
– A·D)·Yk
+ e
сходится при любом начальном приближении
Y0
к единственному решению системы линейных
уравнений A·D·Y
= e
. Таким образом, вектор D·Y
является решением системы A·X
= b
= e
.
(1
j
n),
то ||In
– A·D||1
< 1
для
диагональной
матрицы D
с элементами di
= aii–1
по диагонали. В этом случае итерационный
процесс Yk+1
= (In
– A·D)·Yk
+ e
сходится при любом начальном приближении
Y0
к единственному решению системы линейных
уравнений A·D·Y
= e
. Таким образом, вектор D·Y
является решением системы A·X
= b
= e
.
(3) Любая матрица элементарными преобразованиями строк (столбцов) приводится к виду с диагональным преобладанием по строкам (столбцам). Таким образом, любую систему линейных уравнений A·X = b можно преобразованиями строк привести к виду, пригодному для применения метода простой итерации.
Доказательство.
(1) Если
матрица А
с диагональным
преобладанием по строкам, то матрица
C
= D·A
имеет
элементы ci
j
=
![]() (1
n).
Поэтому для матрицы B
= In
– D·A
при любом
1
i
n
справедливы
равенства bii
= 0,
bij
=
(1
n).
Поэтому для матрицы B
= In
– D·A
при любом
1
i
n
справедливы
равенства bii
= 0,
bij
=
![]() и
и
 ,
так что ||B||
=
,
так что ||B||
=
![]() < 1.
< 1.
Все остальные утверждения следуют из общей теории сжимающих отображений.
(2) Все вычисления для обоснования неравенства ||In – A·D||1 < 1 аналогичны предыдущим. Поэтому при любом начальном приближении Y0 сходится итерационный процесс Yk+1 = (In – A·D)·Yk + e . Переходя к пределу в итерационном соотношении, получим Y = (In – A·D)·Y + e A·D·Y = e. Все остальные утверждения следуют из общей теории сжимающих отображений.
(3) Это очевидно, т.к. обратимую матрицу A можно элементарными преобразованиями строк привести к диагональному виду, который, очевидно, обладает свойствами диагонального преобладания.
Лемма доказана.
Пример. Решить систему с точностью до 0,001:
 .
.

(переписали систему A·X = b в виде X = B·X + e). При этом нетрудно убедиться, что ||B||1 > 1, ||B|| > 1, ||B||2 > 1 (?!), так что метод простой итерации напрямую неприменим.
В то же время,
исходная матрица A
=
 системы удовлетворяет свойству
диагонального преобладания по столбцам.
Поэтому можно воспользоваться леммой
о матрицах с диагональным преобладанием:
D
=
системы удовлетворяет свойству
диагонального преобладания по столбцам.
Поэтому можно воспользоваться леммой
о матрицах с диагональным преобладанием:
D
=
 .
При этом
.
При этом
B
= I4
– A·D
 ,
||B||1
< 1.
,
||B||1
< 1.
Применяем метод простой итерации Yk+1 = (In – A·D)·Yk + b для решения системы A·D·Y = b и находим X = D·Y :
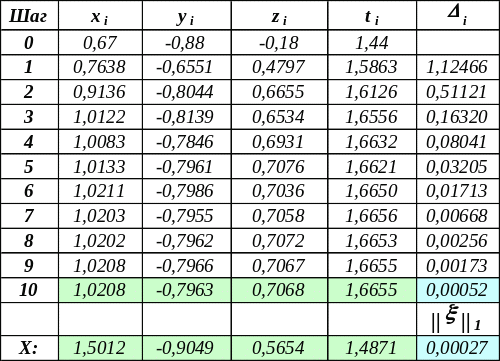
В последней строке этой таблицы приведены решение X исходной системы и норма невязки, соответствующей этому решению.
Замечание: При применении метода простой итерации могут возникнуть проблемы (см., например, [1, стр. 271]), которые состоят в том, что ранее сходимости может случиться переполнение (числа становятся слишком большие даже для ЭВМ). Эти нюансы подробно обсуждать не будем.
Метод Зейделя. Покомпонентная запись метода простой итерации Xn+1 = B·Xn + e приведена в нижеследующих формулах слева. Здесь xj(i) – j-я компонента вектора Xi – приближения, вычисленного на i-й итерации. Метод Зейделя, покомпонентные формулы которого приведены справа допускает использование при вычислении компоненты xi(n+1) вектора Xn+1 уже вычисленных предыдущих его компонент x0(n+1), … , xi–1(n+1).

Для того чтобы записать эти формулы в матричном виде, введём две матрицы, связанные с матрицей B:
 .
.
Тогда метод Зейделя можно записать в матричном виде следующим образом:
Xn+1 = C·Xn+1 + D·Xn + e (In – C)·Xn+1 = D·Xn + e
Xn+1 = (In – C)–1·D·Xn + e.
Здесь матрица In – C – верхнетреугольная с ненулевыми элементами по диагонали, а потому обратима.
Таким образом, формально говоря, метод Зейделя – это частный случай метода простой итерации с матрицей U = (In – C)–1·D. Однако, сходится метод Зейделя, как правило, быстрее. Это утверждение далеко не очевидно, т.к. нельзя даже утверждать, что при выполнении условия ||B|| < 1 будет выполнено условие ||U|| <1.
Пример:
Если B
=
![]() ,
то С =
,
то С =
![]() ,
D
=
,
D
=
![]() и I2
– C
=
и I2
– C
=
![]() ,
(I2
– C)–1
=
,
(I2
– C)–1
=
![]() ,
U
= (I2
– C)–1·D
=
,
U
= (I2
– C)–1·D
=
![]() .
Кроме того, ||B||1
= 0,9 < 1, но
||U||1
= 1,1 > 1.
.
Кроме того, ||B||1
= 0,9 < 1, но
||U||1
= 1,1 > 1.
Таким образом, непосредственно применить изложенную выше теорию не удаётся. Тем удивительнее следующая теорема, доказательство которой можно найти в [9, стр. 235].
Теорема (о методе Зейделя). Если ||B||1 < 1 или ||B|| < 1, то метод Зейделя сходится, причём, как правило, несколько быстрее метода последовательных приближений.
Пример. Решить систему с точностью до 0,001:
.
–
система в виде X = B·X + e, где , и
||B|| = max{0,4+0,2+0,3+0,05; 0,2+0,2+0,3+0,1;
0,05+0,3+0,5+0,1; 0,5+0,1+0,1+0,1} = 0,95 < 1.
Поэтому можно применить метод Зейделя:


Сравнение проведённых вычислений с расчётами по методу простой итерации в первом примере этого параграфа показывает, что в данном случае метод Зейделя сходится хуже. Таким образом, оговорка “как правило” в сформулированной выше теореме не случайна.
