- •Вместо введения: о погрешностях при решении прикладных задач
- •Глава I. Численные методы решения уравнений
- •§ 1. Задача локализации корней
- •Ограничение корней
- •Локализация корней
- •Простейший (грубейший) алгоритм локализации корней:
- •§ 2. Понятие об итерационных методах уточнения корней
- •Метод деления пополам (метод вилки)
- •§ 3. Методы хорд и касательных
- •Метод хорд для монотонных выпукло-вогнутых функций
- •Метод касательных для монотонных выпукло-вогнутых функций
- •§ 4. Метрические и банаховы пространства. Теорема о неподвижной точке
- •Матричные нормы
- •§ 5. Метод простой итерации
- •§ 6. Применение метода простой итерации к решению
- •Условие h([; ]) [; ] :
- •Глава II. Вычисления в линейной алгебре
- •§ 1. Метод Гаусса и его улучшения для повышения точности решения
- •§ 2. Метод простой итерации и метод Зейделя
- •§ 3. Подготовка к применению метода простой итерации
- •§ 4. Проблема собственных значений
- •Глава III. Численное интегрирование
- •§ 1. Метод прямоугольников
- •§ 2. Метод трапеций
- •§ 3. Метод Симпсона (параболическое интерполирование)
- •Глава IV. Некоторые методы аппроксимации функций
- •§ 1. Интерполяционный многочлен Лагранжа
- •§ 2. Интерполяционный многочлен Ньютона
- •§ 3. Метод наименьших квадратов
- •Глава V. Некоторые методы численного решения дифференциальных уравнений
- •Приложение: Сводка характеристик численных методов
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
- •Характеристики метода:
Глава II. Вычисления в линейной алгебре
Речь пойдёт, в основном, о решении систем линейных уравнений вида A·X = b с квадратной невырожденной матрицей A M(n, F). Такие системы можно решать методом Гаусса, который состоит, как известно из курса алгебры, в последовательном приведении расширенной матрицы (A | b) системы A·X = b к каноническому ступенчатому виду. В случае квадратной невырожденной матрицы A каноническая матрица выглядит просто: (In | X), где In – единичная (nn)-матрица, а X – решение системы уравнений.
Вычислительные проблемы с методом Гаусса обусловлены двумя основными обстоятельствами. Первое обстоятельство: метод Гаусса требует достаточно много алгебраических операций. Оценим количество операций. Для обнуления остальных n – 1 элементов каждого столбца за счёт главного элемента этого столбца необходимо:
– произвести одно деление (вычислить обратный элемент к главному),
– выполнить 2·(n – 1)·k умножений (умножить все k ненулевых элементов строки главного элемента на вычисленный обратный и на обнуляемый элемент),
– произвести (n – 1)·k сложений (прибавить k ненулевых элементов сроки главного элемента к каждой из остальных строк).
Таким образом,
всего требуется 1
+ (n
– 1)·[2·k
+ k]
операций в
каждом столбце, а всего для приведения
(nn)-матрицы
к каноническому виду потребуется
n
делений,
![]() = (n
– 1)2·n
умножений
и вполовину меньше сложений, т.е. n
+ 1,5·(n
– 1)2·n
операций.
Видно, что
общее количество операций имеет порядок
n3.
При выполнении большого объёма вычислений
общая погрешность может значительно
возрастать (даже погрешность суммы
оценивается как сумма погрешностей).
Значит, метод
Гаусса даёт не точное, а лишь приближённое
решение системы линейных уравнений,
точность которого может быть далека от
заданной предельной погрешности
вычислений.
= (n
– 1)2·n
умножений
и вполовину меньше сложений, т.е. n
+ 1,5·(n
– 1)2·n
операций.
Видно, что
общее количество операций имеет порядок
n3.
При выполнении большого объёма вычислений
общая погрешность может значительно
возрастать (даже погрешность суммы
оценивается как сумма погрешностей).
Значит, метод
Гаусса даёт не точное, а лишь приближённое
решение системы линейных уравнений,
точность которого может быть далека от
заданной предельной погрешности
вычислений.
Второе обстоятельство
связано с тем, что для
близкой к вырожденной матрицы A
решение
системы A·X
= b
может быть
неустойчивым.
Это значит, что достаточно
малые изменения коэффициентов системы
(погрешности) могут привести к
существенным изменениям решения.
Такая матрица А
называется плохо
обусловленной.
Например, для системы
![]() точным решением будет
точным решением будет
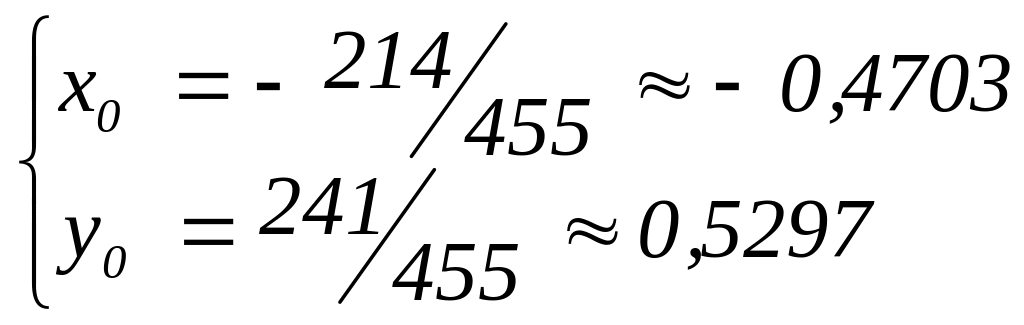 .
Если же допустить абсолютную погрешность
0,01 в
коэффициенте 6,29,
то система
.
Если же допустить абсолютную погрешность
0,01 в
коэффициенте 6,29,
то система
![]() имеет решение
имеет решение
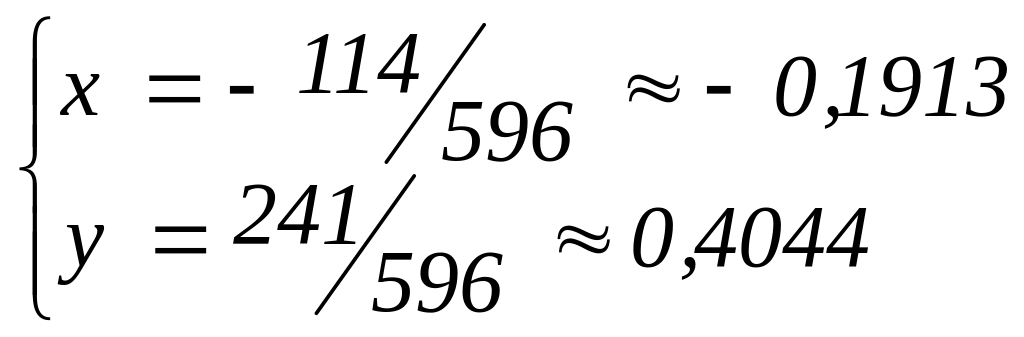 .
Таким образом
.
Таким образом
![]() : абсолютная
погрешность увеличилась в 10 раз.
: абсолютная
погрешность увеличилась в 10 раз.
Таким образом, при решении систем линейных уравнений необходимо учитывать перечисленные факторы и повышать точность решений.
§ 1. Метод Гаусса и его улучшения для повышения точности решения
Рассмотрим решение
системы
 по методу Гаусса в среде Excel.
Конечно, малый размер решаемой системы
не позволяет сделать погрешность
вычислений слишком большой, но даже
приведённый пример показывает, что
вектор-невязка
= A·X
– b
становится ненулевым: величины его
компонент превышают границу погрешности
компьютера.
по методу Гаусса в среде Excel.
Конечно, малый размер решаемой системы
не позволяет сделать погрешность
вычислений слишком большой, но даже
приведённый пример показывает, что
вектор-невязка
= A·X
– b
становится ненулевым: величины его
компонент превышают границу погрешности
компьютера.
Вычисления оформлены естественным образом: над матрицей последовательно производятся элементарные преобразования строк с соответствующими главными элементами. Последние два столбца содержат контрольные суммы: столбец первоначально содержит суммы элементов в столбцах x, y, z и в столбце свободных членов, затем с этими суммами производятся те же элементарные преобразования строк, что и со всей расширенной матрицей. В столбце S на каждом шаге вычисляются суммы элементов столбцов x, y, z и столбца свободных членов. Элементы столбца S не должны существенно отличаться от элементов столбца : в рассмотренном примере они практически совпадают. Столбец решений системы выделен зелёным, а вектор невязки – жёлтым. Выбор главных элементов отмечен голубым цветом.
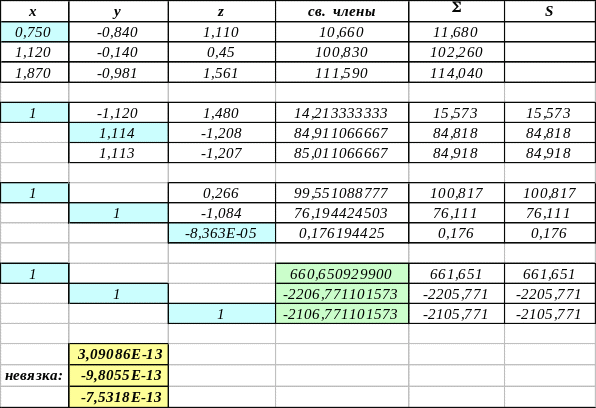
Для уменьшения погрешностей вычисления рекомендуется выбирать главными элементами элементы матрицы с наибольшими модулями. Например, для решённого выше примера вычисления модифицируются так:

Даже этот пример показывает, что компоненты вектора невязки уменьшились по абсолютной величине.
По величине компонент вектора невязки нельзя судить о допущенной в ходе вычислений погрешности решения системы. Найденное решение можно улучшить, если учесть невязку: вместо точного решения X0 системы A·X = b было найдено приближённое решение X, удовлетворяющее равенству A·X = b + . Поэтому можно записать X = X0 + X1 и получить A·X = = b + A·(X0 + X1) = b + A·X1 = – систему уравнений для вектора X1 , решив которую, найдём более точное приближение для решения X = X0 + X1 . Вектор X1 (или его норма) и определяет величину погрешности. Например, для предыдущего решения уточнение приведёт к следующим вычислениям:
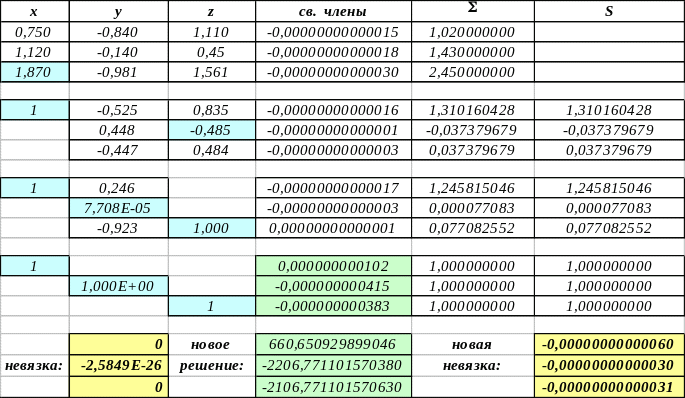
которые уже позволяют судить о допущенной погрешности, имеющей порядок 10–8. При необходимости подобные улучшения могут проводиться несколько раз. Для данного примера, как показывает следующая таблица, произведённые улучшения несущественны, поскольку точность вычисления в среде Excel и так достаточно высока.