Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

“Тобольская государственная педагогическая академия

им. Д.И. Менделеева”

Кафедра математики и ТиМОМ

Валицкас А.И.

КОНСПЕКТ ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ

“ЧИСЛЕННЫЕ МЕТОДЫ”

Тобольск – 2009

С О Д Е Р Ж А Н И Е

ПРЕДИСЛОВИЕ	. . . . . . . . . . . . . .	3
ВМЕСТО ВВЕДЕНИЯ	О погрешностях при решении прикладных задач .	4
Глава I.	ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЙ	11
	§ 1. Задача локализации корней . . . . .	11
	§ 2. Понятие об итерационных методах уточнения корней . . . . . . . . . .	17
	§ 3. Методы хорд и касательных . . . .	22
	§ 4. Метрические и банаховы пространства. Теорема о неподвижной точке . . . . .	31
	§ 5. Метод простой итерации . . . . .	42
	§ 6. Применение метода простой итерации к решению уравнения f(x) = 0 . . . . . .	48
Глава II.	ВЫЧИСЛЕНИЯ В ЛИНЕЙНОЙ АЛГЕБРЕ . .	54
	§ 1. Метод Гаусса и его улучшения для повышения точности решения . . . . . . . .	55
	§ 2. Метод простой итерации и метод Зейделя .	58
	§ 3. Подготовка к применению метода простой итерации . . . . . . . . . .	66
	§ 4. Проблема собственных значений . . .	72
Глава III.	ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ . . . .	73
	§ 1. Метод прямоугольников . . . . . .	73
	§ 2. Метод трапеций . . . . . . . .	76
	§ 3. Метод Симпсона (параболическое интерполирование) . . . . . . . . .	79
Глава IV.	НЕКОТОРЫЕ МЕТОДЫ АППРОКСИМАЦИИ ФУНКЦИЙ . . . . . . . . . .	87
	§ 1. Интерполяционный многочлен Лагранжа . .	88
	§ 2. Интерполяционный многочлен Ньютона . .	96
	§ 3. Метод наименьших квадратов . . . . .	103
Глава V.	НЕКОТОРЫЕ МЕТОДЫ ЧИСЛЕННОГО РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ . . .	114
ЛИТЕРАТУРА	. . . . . . . . . . . . . .	115
ПРИЛОЖЕНИЕ	Сводка характеристик численных методов . .	116

П Р Е Д И С Л О В И Е

Вместо введения: о погрешностях при решении прикладных задач

Решение любой прикладной задачи проходит, как правило, следующие основные этапы:

• построение математической модели;

• выбор метода (приближённого) решения полученной математической задачи;

• вычисления (как правило, на ЭВМ);

• анализ полученных результатов.

На каждом из первых трёх этапов возможно появление погрешностей, которые называются погрешностями модели, метода, и вычислений. Расчёты на ЭВМ связаны с ещё одним специфическим видом погрешностей – погрешностью разрядной сетки, связанной с ограниченностью разрядности ЭВМ и представлением чисел в ЭВМ. Таким образом, общая погрешность решения задачи будет суммой этих четырёх погрешностей.

Замечания: 1. Наука изучает не реальный мир, а математические модели, лишь приближённо отражающие реальность. Можно ли после этого говорить о непогрешимой точности научной методологии ?

2. Чистая математика не обусловлена потребностью практики: для решения любой прикладной задачи нет нужды искать точное решение, всегда достаточно ограничиться лишь некоторым приближением к нему.

Наиболее существенная из погрешностей – погрешность модели – обсуждаться в дальнейшем не будет, хотя неправильный выбор математической модели реального процесса может свести на нет все усилия по решению задачи. Не будет обсуждаться и погрешность разрядной сетки, т.к. это требует специальных знаний по представлению чисел в ЭВМ. Основное внимание пока уделим погрешности вычислений, а погрешность метода будет анализироваться позднее при изучении конкретных методов приближённого решения математических задач.

Если известно точное значение x₀ некоторой величины и вычислено её приближённое значение x, то можно ввести абсолютную погрешность (x) = |x – x₀ | и относительную погрешность (x) = , которая, будучи умноженной на 100, показывает процент отклонения абсолютной погрешности от величины |x|. Как правило, точное значение вычисляемой величины неизвестно. Поэтому при приближённых вычислениях пользуются лишь верхними границами  и  абсолютной и относительной погрешностей или их более или менее грубыми оценками.

Пример: Значение x = 1,4 даёт приближение величины x₀ = с абсолютной погрешностью  = |1,4 – 1,414213562373095048801688… | = = 0,014213562373095048801688… < 0,15 и относительной погрешностью  = = 0,010152544552210749144063… < < 0,011 ( 1,1 %).

Этот пример показывает, что даже знание точного результата не позволяет вычислить значения абсолютной и относительной погрешностей без округлений. Запись x = x₀ ±  в дальнейшем будет означать, что выполнены неравенства x₀ –   x x₀ + , т.е. абсолютная погрешность величины x по отношению к точному значению x₀ не превосходит .

Основной вопрос, исследуемый в дальнейшем: как ведут себя погрешности при выполнении арифметических действий ?

Лемма (о погрешностях при вычислении функций). (1) Если известно, что x = x₀ ± (x) , y = y₀ ± (y) , то

(x ± y)  (x) + (y), (x ± y)  ,

(x·y)  |y|·(x) + |x|·(y) + (x)·(y), (x·y)  (x) + (y) + (x)·(y),

,

.

(2) Пусть в некотором параллелепипеде П: a_i  x_i  b_i (1  i  n) задана непрерывно дифференцируемая функция F(x) = F(x₁ , … , x_n) со значениями в R (т.е. все её частные производные (x) непрерывны в каждой точке открытого параллелепипеда П⁰: a_i < x_i < b_i (1  i  n)). Тогда для любых x_i = a⁰_i ± _i  (a_i ; b_i) (1  i  n) найдётся некоторая точка с  П со свойством .

(3) Из (2) следует, что |F(x) – F(a⁰)|  , т.е. верна оценка F(x) = F(a⁰ ) ± , где M_i = , или F(x)  . В частности, F(x) = F(a⁰ ) ± n·M··, где M = ,  = , или F(x)  n·M· .

Доказательство. (1) Все оценки доказываются однообразно с использованием неравенств для модулей:

(x ± y) =|(x ± y)–(x₀ ± y₀)| = |(x–x₀)±(y–y₀)|  |x–x₀| + |y–y₀| = (x) + (y),

,

(x·y) = |x·y – x₀·y₀ | = |(x – x₀)·y + x·(y – y₀ ) + (x₀ – x)·(y – y₀ )| 

 |x – x₀ |·|y| + |x|·|y – y₀ | + |x₀ – x|·|y – y₀ | = |y|·(x) + |x|·(y) + (x)·(y),

(x·y) = = (x) + (y) + (x)·(y),

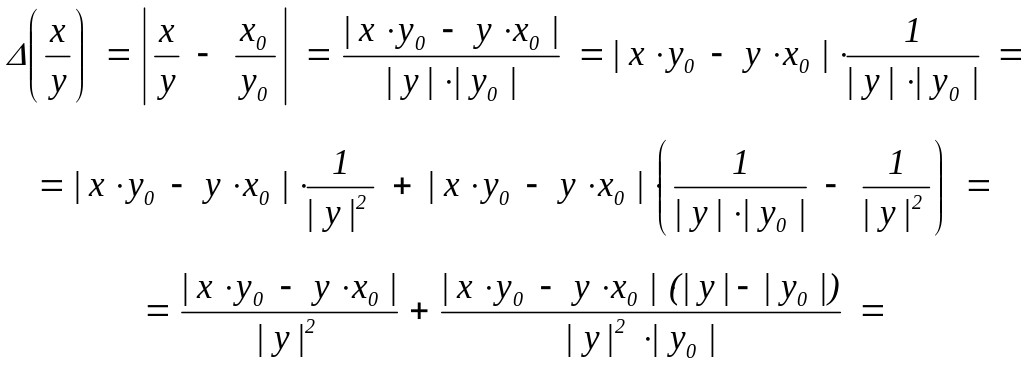
(2) По функции F(x₁ , … , x_n ) построим вспомогательную действительную функцию

G(t) = (F(x)–F(a⁰))·t – F(a⁰₁ + t·(x₁ – a⁰₁), … , a⁰_n + t·(x_n – a⁰_n)),

определённую для t  [0; 1]. Тогда G(0) = –F(a⁰) = G(1), и значит, найдётся такое t₀  [0; 1], что G(t₀) = 0, т.е.

0 = G(t₀) = F(x) – F(a⁰) – ,

где c_i = a⁰_i + t₀·(x_i – a⁰_i) (1  i  n).

(3) Дальнейшие оценки очевидны: F(x) = |F(x) – F(a⁰) | =

=  n·M· .

Теорема доказана.

Замечания: 1. Относительная погрешность суммы или разности может весьма значительно отличаться от относительных погрешностей слагаемых. Например, если x = 0,8 и y = 0,9 – два приближения для x₀ = 1 = y₀ , то (x) = = 0,25, (y) = = 0,(1), но для приближения x – y = –0,1 величины x₀ – y₀ = 0 будет выполнено равенство (x – y) = = 1.

2. Абсолютная погрешность частного может весьма значительно отличаться от абсолютных погрешностей делимого и делителя. Например, если x = 0,11 и y = 0,09 – приближения величин x₀ = 0,1 = y₀ , то (x) = 0,01 = (y), но = 1,(2) и  = 0,(2). Величина абсолютной погрешности увеличилась в 20 раз !

3. Если величины (x), (y), (x), (y) малы как по величине, так и по сравнению с |x|, |y|, то в полученных в лемме оценках для произведения и частного можно пренебречь членами второго порядка малости, т.е. можно считать:

(x·y)  |y|·(x) + |x|·(y), (x·y)  (x) + (y),

, .

Конечно, эти неравенства не являются точными: они могут нарушаться, но лишь на величины второго порядка малости.

Полученные в лемме оценки позволяют определять количество верных цифр результата приближённых вычислений. Цифра результата называется верной, если абсолютная погрешность результата не превосходит половины единицы разряда, в котором стоит эта цифра: цифра c_k десятичного числа x = c_m … c₀ , c_–1 … c_–s … верна, если  = (x)  0,510^–k.

Примеры: 1. При округлении числа x₀ = 1,987654 до x = 1,99 получается абсолютная погрешность (x) = |x – x₀| = 0,002346, так что обе цифры верны: (x) = 0,002346 < 0,5·0,01 = 0,005.

При округлении того же числа x₀ = 1,987654 до x = 1,98766 абсолютная погрешность будет (x) = |x – x₀| = 0,000006, и последняя цифра уже не верна, поскольку (x) = 0,000006 > 0,5·0,00001 = 0,000005.

2. Пусть даны два числа x = 1,154 и y = 2,010, заданные верными цифрами. На калькуляторе вычислили их частное = 0,5741. Сколько в нём правильных цифр ?

Подсчитаем абсолютную погрешность частного, учитывая, что (x) = = (y) = 0,0005 (из неравенств (x)  0,5·0,001, (y)  0,5·0,001):

.

Таким образом, если считать , то в результате 0,5741 верны три цифры после запятой: 0,000392  0,5·0,001 = 0,0005, четвёртая же цифра может оказаться неверной.

Можно действовать по-другому: из 2,010 – (y)  y  2,010 + (y) получаем

.

Как видим, и при таком подходе границы результата отличаются в десятитысячных, а первые три цифры после запятой неизменны.

Значит, в результате = 0,5741 верны три цифры после запятой.

3. Пусть даны два числа x = 1,154 и y = 0,010, заданные верными цифрами. На калькуляторе вычислили их частное = 115,4000. Сколько в нём правильных цифр ?

Аналогично предыдущему вычислим абсолютную погрешность частного, учитывая, что (x) = (y) = 0,0005 :

.

Таким образом, если считать , то в результате 115,4000 можно доверять лишь первой цифре: сотням.

Можно действовать по-другому: из 0,010 – (y)  y  0,010 + (y) получаем

.

Как видим, и при таком подходе границы результата отличаются уже в цифре десятков.

Таким образом, в результате = 115,4000 верна только цифра сотен.

4. С какой точностью нужно округлить x₀ = 0,587964 до величины x, чтобы значение sin x совпало в трёх цифрах после запятой со значением sin x₀ ?

Ясно, что должно выполняться неравенство |sin x – sin x₀ | < 0,0005, т.е.  sin x < 0,0005. По теореме о погрешности для F(x) = sin x имеем . Значит, для выполнения неравенства F(x) < 0,0005 нужно взять  x < . На интервале [0,5; 0,6] максимум знаменателя достигается при x = 0,5 (т.к. cos x убывает на этом интервале). Значит,

 x < , 0,587854 < x < 0,588074.

Нетрудно убедиться, что в указанном промежутке действительно три цифры после запятой числа sin x совпадают с цифрами числа sin x₀ :

sin 0,587854  0,554577, sin 0,588074  0,554760,

sin 0,587964  0,554668.