2. Решение задач нелинейного программирования cредствами Excel

Решение задачи нелинейного программирования отличается от решения задачи линейного программирования следующим:

• назначаются начальные значения искомых переменных;

• в диалоговом окне Параметры поиска решения не надо вводить Линейная модель.

Начальные значения желательно назначать близкими к ожидаемым оптимальным значениям, что ускорит решение задачи (часто их принимаются равными единице). Обязательное требование заключается в том, чтобы целевая функция в начальной точке не была равной нулю.

Решение задачи НЛП в Excel рассмотрим на следующих примерах:

Пример 1. Минимизировать

f(X) = x₁² + x₂² + x₃²

при ограничениях g₁(X) = x₁ + x₂ + 3x₃ – 2 = 0,

g₂(X) = 5x₁ + 2x₂ + x₃ – 5 = 0.

1. Создадим форму для ввода условий задачи (рис. 2.1) и введем:

• зависимости для целевой функции и ограничений;

• начальные значения переменных, равные единице;

• правые части ограничений.

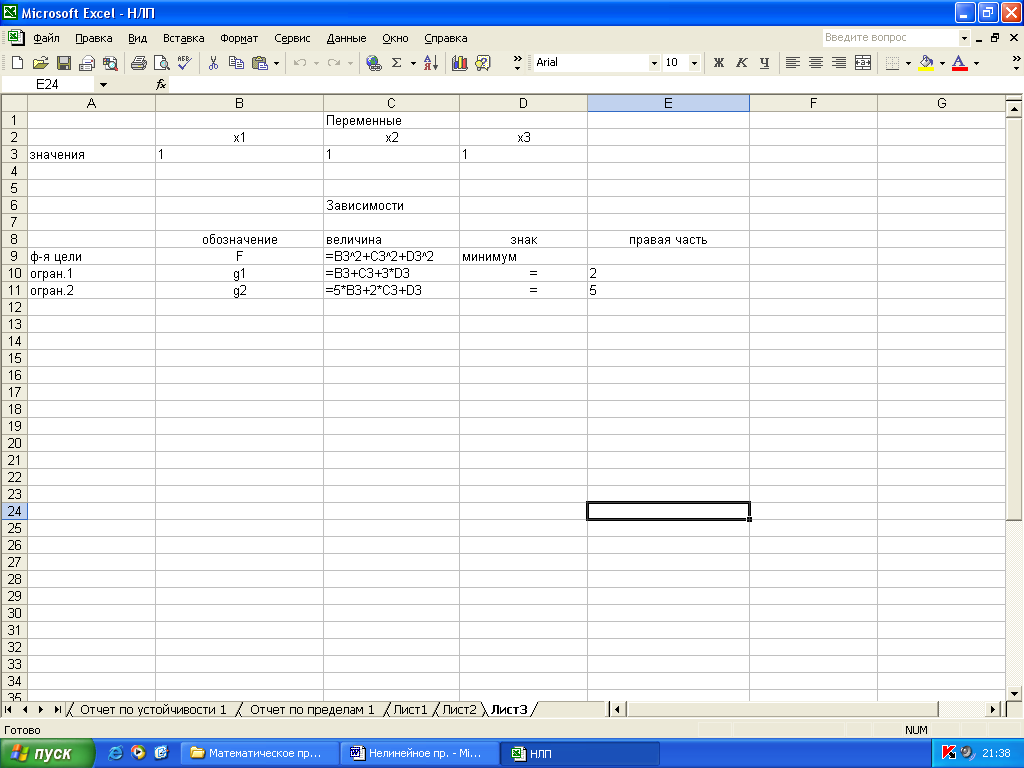
Рис. 2.1

2. Сервис, Поиск решения…

На экране: диалоговое окно Поиск решения (рис. 2.2).

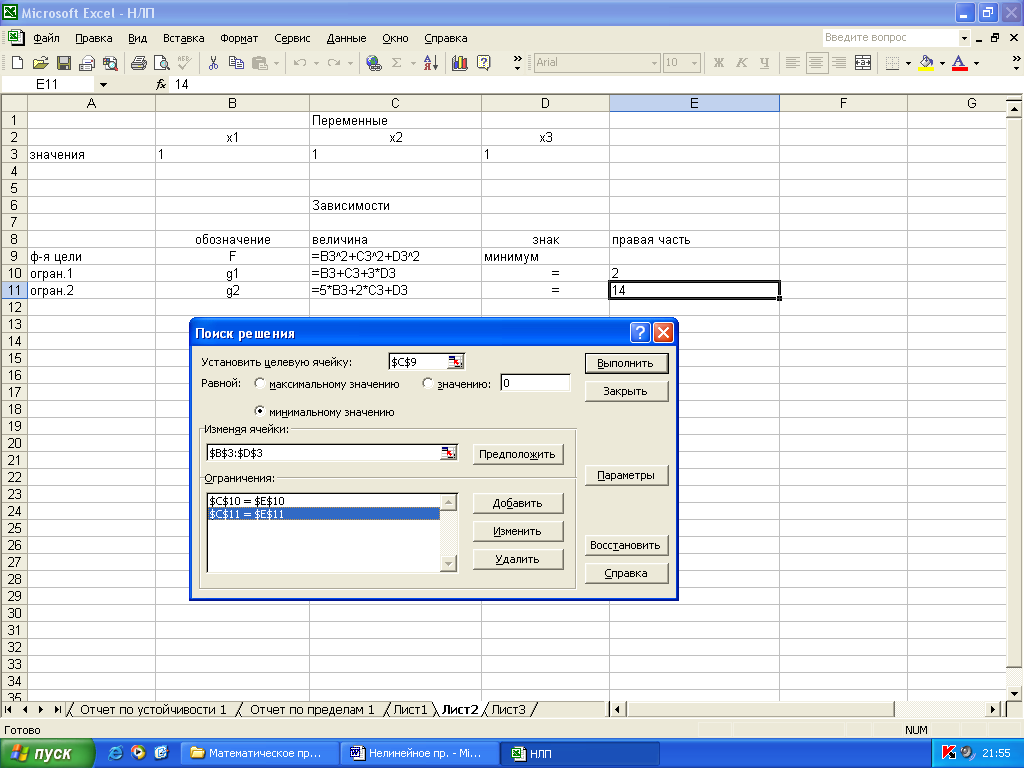
Рис. 2.2.

3. Введем:

• целевую функцию С9; минимизировать;

• изменяемые ячейки В3:D3;

• ограничения С10 = Е10; С11 = Е11.

4. Перейдем к решению задачи. Выполнить.

На экране: результат решения (рис. 2.3).

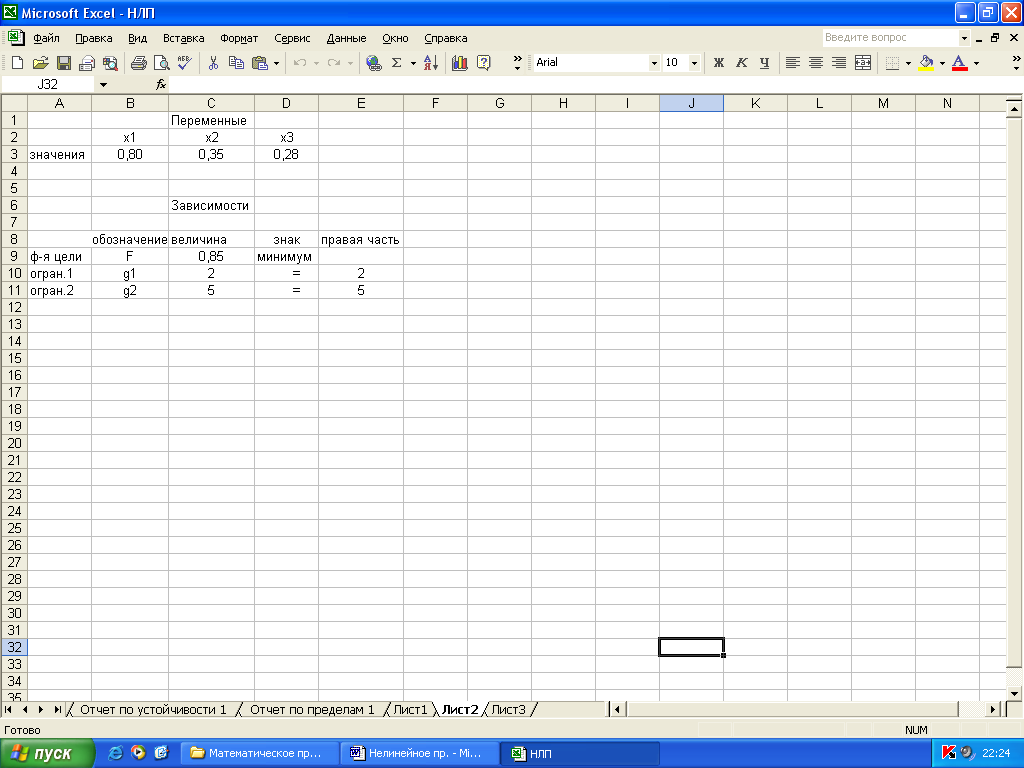
Рис. 2.3.

Получено решение: х₁ = 0,8; х₂ = 0,35; х₃ = 0,28; F_min = 0,85.

После успешного завершения поиска решения на экране появляется диалоговое окно Результаты поиска решения. С помощью этого диалогового окна можно вызвать отчеты трех типов:

• результаты;

• устойчивость;

• пределы.

Среди них только Отчет по устойчивости (рис. 2.4) отличается от аналогичных результатов для задачи линейного программирования.

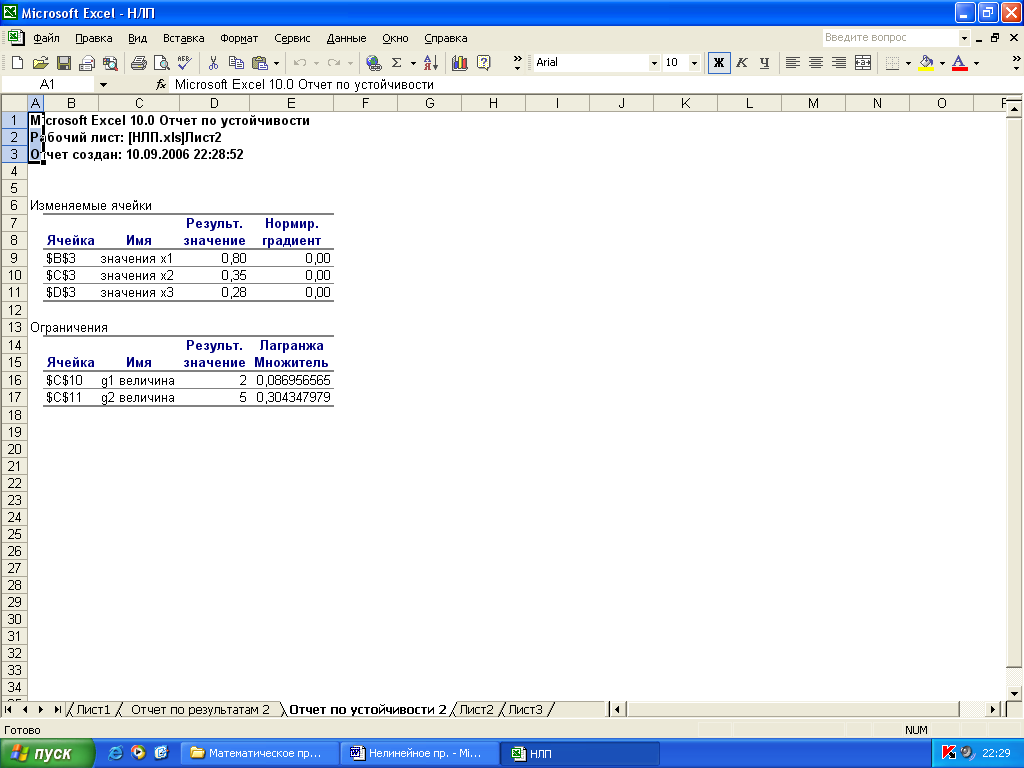
Рис. 2.4.

Отчет по устойчивости состоит из двух таблиц.

В таблице 1 приводятся значения для переменных:

• результат решения задачи;

• нормированный градиент – величина, приводимая при выборе некоторых методов в диалоговом окне Параметры поиска решения.

В таблице 2 приводятся значения для ограничений:

• величина правых левой части каждого ограничения (2 и 5 соответственно);

• множитель Лагранжа – аналог двойственной оценки в задаче линейного программирования, который показывает, как изменится целевая функция при изменении правой части ограничения на единицу.

Если решается задача НЛП с ограничениями – неравенствами следует при введении зависимостей по ограничениям ввести соответствующие знаки.

Пример 2. Минимизировать

f(X) = x₁² + x₂² + x₃²

при ограничениях:

g₁ (X) = 2x₁ + x₂ – 5 ≤ 0,

g₂ (X) = x₁ + x₃ – 2 ≤ 0,

g₃ (X) = 1 – x₁ ≤ 0,

g₄ (X) = 2 – x₂ ≤ 0,

g₅ (X) = –x₃ ≤ 0.

На листе Excel создадим форму, в которую введем исходные данные и формулы, определяющие зависимости (рис. 2.5).

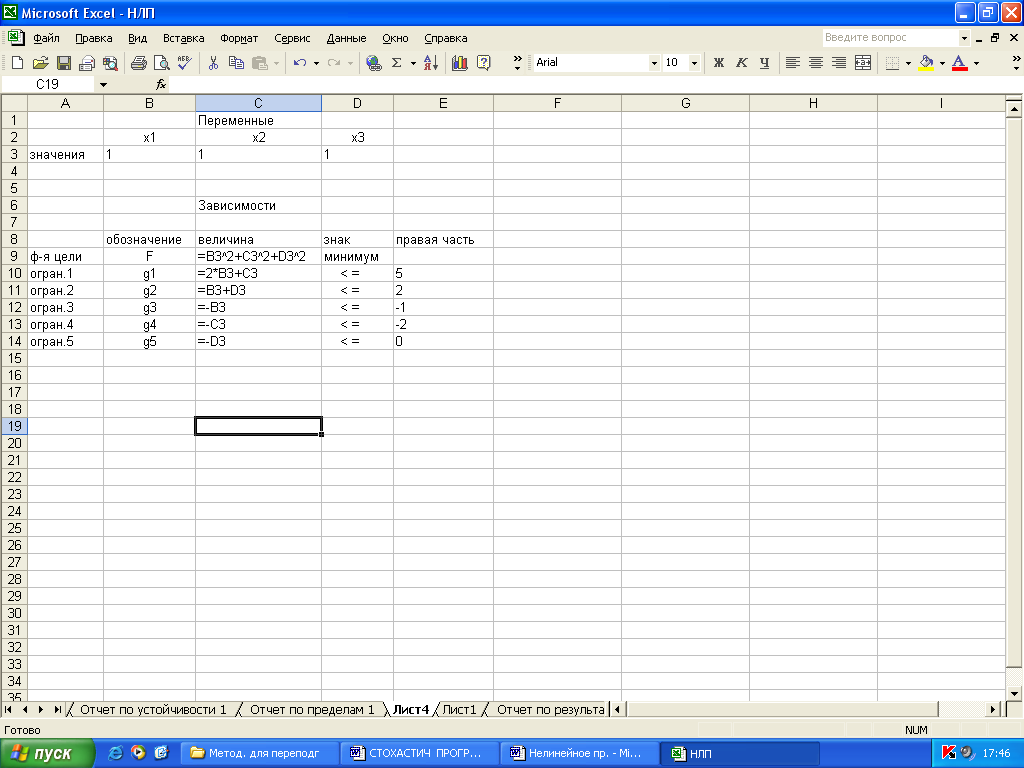
Рис. 2.5.

Обратимся к Поиску решения (рис. 2.6).

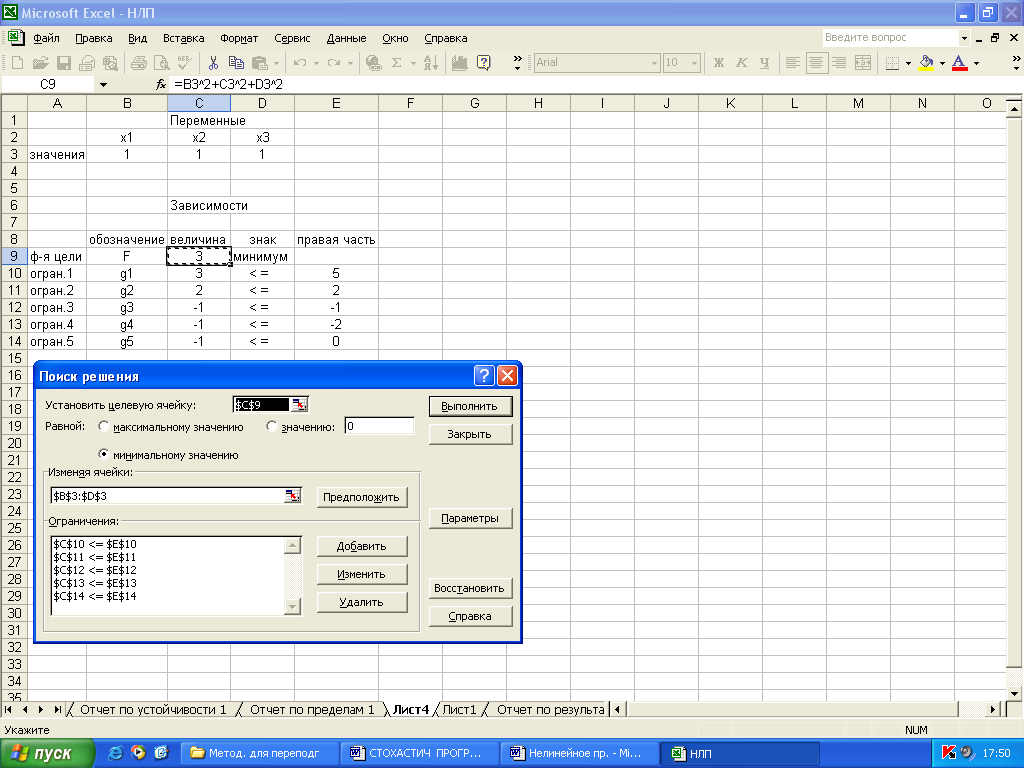
Рис. 2.6.

После команды Выполнить получим результат (рис. 2.7):

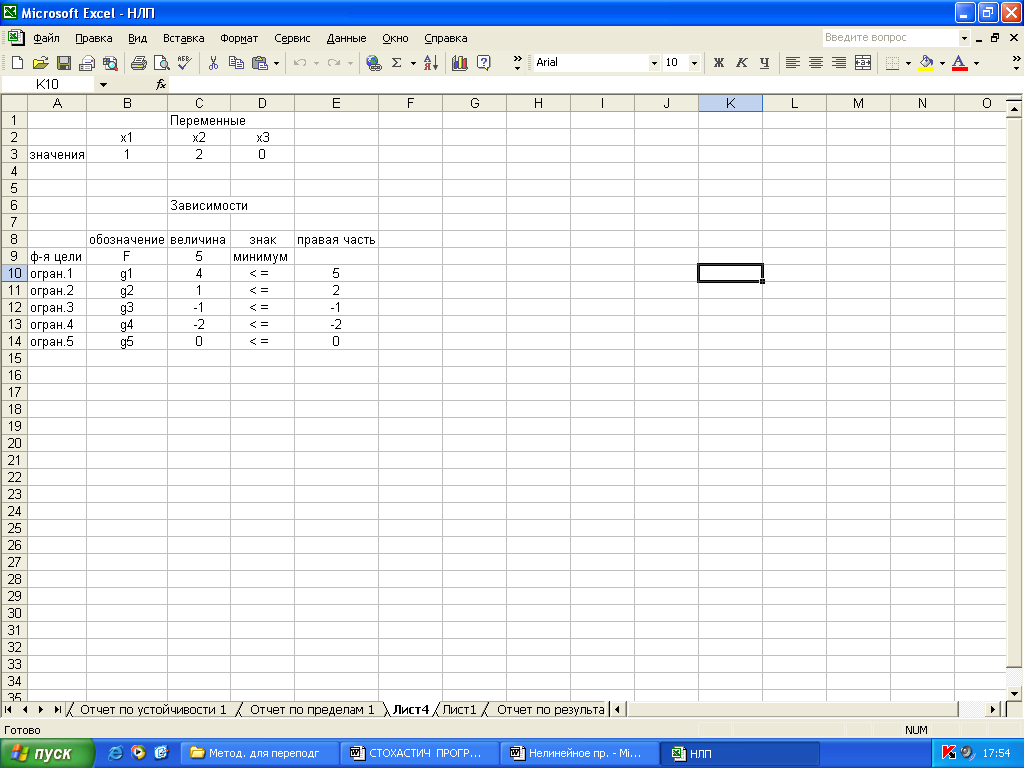
Рис. 2.7.

Оптимальное решение: х₁ = 1, х₂ = 1, х₃ = 1; F_min = 5.