4. Теория графов

Компьютерная сеть соединяет 2 компьютера: источник I со стоком S. Имеется несколько путей, по которым можно выполнить передачу данных из источника в сток. Вершины сети соответствуют пере­сечениям кабеля, а ребра и дуги - участкам сети между пересечения­ми. На сети указаны пропускные способности участков сети, т.е. максималь­ное количество информации, которое можно пропустить по трубам за 1 ч. Какой максимальный поток информации можно передать по данной сети?

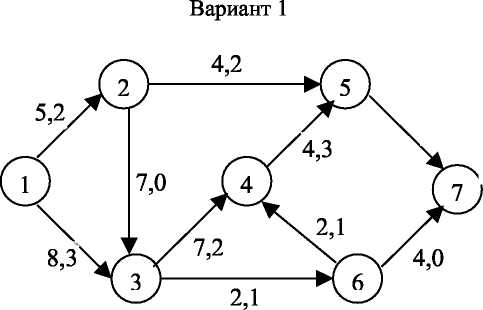
2,6

Рис. 4.1.

Занесенные данные в таблицу. В ячейке таблицы запишем пропускную способность дуги из Pi в Pj пункт. Элемент таблицы (i,j) это способность передачи от Pi к Pj. Элемент (i,j) пропускная способность дуги в обратном направлении.

Таблица 4.1

	1	2	3	4	5	6	7
1		5,2-	8,3
2	0+		7,0-		4,2
3	0	0+		7,2		2,1-
4			0		4,3	0
5		0		0			2,7
6			0+	2,1			4,0-
7					0	0+

Выберем произвольно один из возможных путей от Р0 к Р7

Р1:Р2:Р3:Р6:Р7

Элементы (1,2)(2,3)(3,6)(6,7) отметим в таблице знаком (-).

Элементы (2,1)(3,2)(6,3)(7,6) отметим в таблице знаком (+).

Определим пропускную способность выбранного пути:

Х1= min {(5,2),(7,0),(2,1),(4,0)}=2,1

Вычитаем Х1 из ячеек со знаком (-) и прибавляем со знаком (+).

Таблица 4.2

	1	2	3	4	5	6	7
1		3,1	8,3-
2	2,1		4,9		4,2
3	0+	2,1		7,2-		0
4			0+		4,3-	0
5		0		0+			2,7-
6			2,1	2,1			1,9
7					0+	2,1

Р1:Р3:Р4:Р5:Р7

Элементы (1,3)(3,4)(4,5)(5,7) отметим в таблице знаком (-).

Элементы (3,1)(4,3)(5,4)(7,5) отметим в таблице знаком (+).

Х1= min {(8,3),(7,2),(4,3),(2,7)}=2,7

Таблица 4.3

	1	2	3	4	5	6	7
1		3,1	5,6
2	2,1		4,9		4,2
3	2,7	2,1		4,5		0
4			2,7		1,6	0
5		0		2,7			0
6			2,1	2,1			1,9
7					2,7	2,1

Из первой таблицы нужно вычесть последнюю, отрицательные числа не записывать.

Таблица 4.4

	1	2	3	4	5	6	7
1		2,1	2,7
2	2,1		2,1		0
3				2,7		2,1
4					2,7	0
5		0					2,7
6				0			2,1
7

С= 2,1+2,7=4,8

Р1:Р2:Р3:Р6:Р7

2

7

1

3 6

рис. 4.2 Теория графов

Р1:Р3:Р4:Р5:Р7

5

1

4 7

3

рис. 4.3 Теория графов

Ответ: максимальный поток равен 4,8.