Знакочередующиеся ряды. Признак Лейбница. Примеры решений

Для того чтобы понять примеры данного урока необходимо хорошо ориентироваться в положительных числовых рядах: понимать, что такое ряд, знать необходимый признак сходимости ряда, уметь применять признаки сравнения, признак Даламбера, признаки Коши. Тему можно поднять практически с нуля, последовательно изучив статьи Ряды для чайникови Признак Даламбера. Признаки Коши. Логически этот урок является третьим по счёту, и он позволит не только разобраться в знакочередующихся рядах, но и закрепить уже пройденный материал! Какой-то новизны будет немного, и освоить знакочередующиеся ряды не составит большого труда. Всё просто и доступно.

Что такое знакочередующийся ряд? Это понятно или почти понятно уже из самого названия. Сразу простейший пример.

Рассмотрим ряд   и распишем его подробнее:

А сейчас будет убийственный комментарий. У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности. Знакочередование обеспечивает множитель  : если   чётное, то будет знак «плюс», если нечётное – знак «минус». На математическом жаргоне эта штуковина называется «мигалкой». Таким образом, знакочередующийся ряд «опознается» по минус единичке в степени «эн».

В практических примерах знакочередование членов ряда может обеспечивать не только множитель  , но и его родные братья:  ,  ,  , …. Например:

Подводным камнем являются «обманки»:  ,  ,   и т.п. – такие множители не обеспечивают смену знака. Совершенно понятно, что при любом натуральном  :  ,  ,  . Ряды с обманками подсовывают не только особо одаренным студентам, они время от времени возникают «сами собой» в ходе решенияфункциональных рядов.

Как исследовать знакочередующийся ряд на сходимость? Использовать признак Лейбница. Про немецкого гиганта мысли Готфрида Вильгельма Лейбница я рассказывать ничего не хочу, так как помимо математических трудов, он накатал несколько томов по философии. Опасно для мозга.

Признак Лейбница: Если члены знакочередующегося ряда убывают по модулю, то ряд сходится.

Или в два пункта:

1) Ряд является знакочередующимся.

2) Члены ряда убывают по модулю. То есть,  .

Если выполнены оба условия, то ряд сходится.

Справка для тех, кто забыл, что такое модуль:

Что значит «по модулю»? Модуль, как мы помним со школы, «съедает» знак «минус». Вернемся к ряду  . Мысленно сотрём все знаки и посмотрим только на числа. Мы увидим, что каждый следующий член ряда меньше, чем предыдущий. Таким образом, следующие фразы обозначает одно и то же:

– Члены ряда без учёта знака убывают. – Члены ряда убывают по модулю. – Члены ряда убывают по абсолютной величине. – Модуль общего члена ряда стремится к нулю: 

Конец справки

Пример 1

Исследовать ряд на сходимость 

В общий член ряда входит множитель  , а значит, нужно использовать признак Лейбница

1) Проверка ряда на знакочередование. Обычно в этом пункте решения ряд расписывают подробно    и выносят вердикт «Ряд является знакочередующимся».

2) Убывают ли члены ряда по модулю? Необходимо решить предел  , который чаще всего является очень простым.

 – члены ряда не убывают по модулю.

Вывод: ряд расходится.

Как разобраться, чему равно  ? Очень просто. Как известно, модуль уничтожает минусы, поэтому для того, чтобы составить  , нужно просто убрать с крыши проблесковый маячок. В данном случае общий член ряда  . Тупо убираем «мигалку»: 

Пример 2

Исследовать ряд на сходимость 

Используем признак Лейбница:

1)  Ряд является знакочередующимся.

2)   – члены ряда убывают по модулю.

Вывод: ряд сходится.

Всё бы было очень просто – но это еще не конец решения!

Если ряд сходится по признаку Лейбница, то также говорят, что ряд сходится условно.

Если сходится и ряд, составленный из модулей:  , то говорят, что ряд сходится абсолютно.

Поэтому на повестке дня второй этап решения типового задания – исследование знакочередующегося ряда на абсолютную сходимость.

Я не виноват – такая уж теория числовых рядов =)

Исследуем наш ряд на абсолютную сходимость. Составим ряд из модулей – опять просто убираем множитель, который обеспечивает знакочередование:   – расходится (гармонический ряд).

Таким образом, наш ряд не является абсолютно сходящимся. Исследуемый ряд    сходится только условно.

Заметьте, что в Примере №1 второй этап не нужен, поскольку еще на первом шаге сделан вывод о том, что ряд расходится.

Собираем ведёрки, лопатки, машинки и выходим из песочницы. Рассматривать более содержательные примеры из кабины экскаватора.

Пример 3

Исследовать ряд на сходимость 

Используем признак Лейбница:

1)  Данный ряд является знакочередующимся.

2)   – члены ряда убывают по модулю.

Вывод: Ряд сходится.

Исследуем ряд на абсолютную сходимость:

Анализируя начинку ряда, приходим к выводу, что здесь нужно использовать предельный признак сравнения. Скобки в знаменателе удобнее раскрыть:

Сравним данный ряд со сходящимся рядом  . Используем предельный признак сравнения.

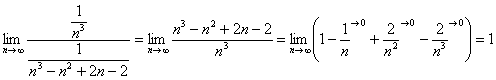
Получено конечное число, отличное от нуля, значит, ряд   сходится вместе с рядом  .

Исследуемый ряд сходится абсолютно.

Готово.

Пример 4

Исследовать ряд на сходимость 

Пример 5

Исследовать ряд на сходимость 

Это примеры для самостоятельного решения. Полное решение и образец оформления в конце урока.

Как видите, знакочередующиеся ряды – это просто и занудно! Но не спешите закрывать страницу, всего через пару экранов мы рассмотрим случай, которых многих ставит в тупик. А пока еще пара примеров для тренировки и повторения.

Пример 6

Исследовать ряд на сходимость 

Используем признак Лейбница.  1) Ряд является знакочередующимся. 2) 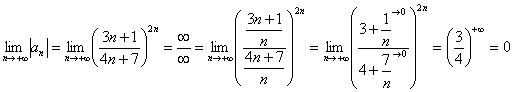   Члены ряда убывают по модулю. Вывод: ряд сходится.

Обратите внимание, что я не расписал подробно члены ряда. Их всегда желательно расписывать, но от непреодолимой лени в «тяжелых» случаях можно ограничиться фразой «Ряд является знакочередующимся». Кстати, не нужно относиться к этому пункту формально,всегда проверяем (хотя бы мысленно) что ряд действительно знакочередуется. Беглый взгляд подводит, и ошибка допускается «на автомате». Помните об «обманках»  ,  ,  , если они есть, то от них нужно избавиться, получив «обычный» ряд с положительными членами.

Исследуем ряд на абсолютную сходимость:

Очевидно, что нужно использовать радикальный признак Коши:

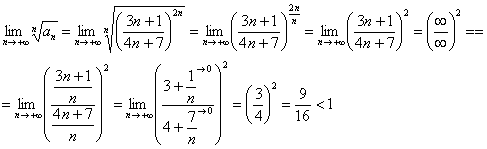
Таким образом, ряд   сходится.

Исследуемый ряд сходится абсолютно.

Пример 7

Исследовать ряд на сходимость 

Это пример для самостоятельного решения. Хммм… что-то я немного погорячился на счет простоты.

Нередко встречаются знакочередующиеся ряды, которые вызывают затруднения.

Пример 8

Исследовать ряд на сходимость 

Используем признак Лейбница: 1) Ряд является знакочередующимся.

2)   

Дело в том, что не существует стандартных обыденных приемов для решения подобных пределов. Куда стремится такой предел? К нулю, к бесконечности? Здесь важно, ЧТО на бесконечности растёт быстрее – числитель или знаменатель. Если числитель   при   растёт быстрее факториала, то  . Если, на бесконечности факториал растёт быстрее числителя, то он, наоборот – «утянет» предел на ноль:  . А может быть этот предел равен какому-нибудь отличному  от нуля числу?

Попробуем записать несколько первых членов ряда:

Создается стойкое впечатление, что  , но где гарантия, что при очень больших «эн» факториал не «обгонит» числитель и не утащит предел на ноль?

Обратимся к теории математического анализа, там давно всё доказано.

Справка

– Факториал растёт быстрее, чем любая показательная последовательность, иными словами:   или  . Да хоть миллион в степени «эн», это не меняет дела. Математики говорят, что факториал более высокого порядка роста, чем любая показательная последовательность.

– Факториал растёт быстрее, чем любая степенная последовательность или многочлен, иными словами:   или  . Вместо   можно подставить какой-нибудь многочлен тысячной степени, это опять же не изменит ситуацию – рано или поздно факториал всё равно «перегонит» и такой страшный многочлен. Факториал более высокого порядка роста, чем любая степенная последовательность.

– Факториал растёт быстрее, чем произведение любого количества показательных и степенных последовательностей (наш случай).

– Любая показательная последовательность растёт быстрее, чем любая степенная последовательность, например:  ,  . Показательная последовательность более высокого порядка роста, чем любая степенная последовательность. Аналогично факториалу, показательная последовательность «перетягивает» произведение любого количества любых степенных последовательностей или многочленов: 

Конец справки

Таким образом, второй пункт исследования (вы еще об этом помните? =)) можно записать так: 2)  , так как   более высокого порядка роста, чем  . Члены ряда убывают по модулю.

Вывод: ряд сходится.

Исследуем ряд на абсолютную сходимость:

А здесь уже работает старый добрый признак Даламбера:

Используем признак Даламбера:

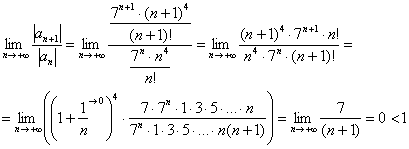
Таким образом, ряд   сходится.

Исследуемый ряд сходится абсолютно.

Разобранный пример можно решить другим способом.

Теорема: Если ряд сходится абсолютно, то он сходится и условно.

Наверное, вы уже заметили, что обратное неверно: если ряд сходится условно, то это еще не значит, что он сходится абсолютно.

Пример 8 «на бис» вторым способом.

Исследовать ряд на сходимость 

Решение: Исследуем ряд на абсолютную сходимость:

Используем признак Даламбера: … только что печатал … Таким образом, ряд   сходится. По соответствующей теореме из абсолютной сходимости ряда следует и условная сходимость ряда.

Вывод: Исследуемый ряд сходится абсолютно.

Правда, при втором способе решения есть риск, что преподаватель оценит хитро… смекалку студента и забракует задание. А может и не забракует.

И напоследок пара примеров для самостоятельного решения. Один из той же оперы (перечитайте справку), но попроще. Другой для гурманов – на закрепление интегрального признака сходимости. 

Пример 9

Исследовать ряд на сходимость 

Пример 10

Исследовать ряд на сходимость 

После качественной проработки числовых положительных и знакопеременных рядов с чистой совестью можно перейти к функциональным рядам, которые не менее монотонны и однообразны интересны.

Желаю успехов!

Решения и ответы:

Пример 4: Используем признак Лейбница:

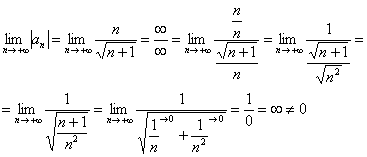1)  Данный ряд является знакочередующимся. 2)    Члены ряда не убывают по модулю. Вывод: Ряд расходится. Примечание: В данном примере неопределенность   устраняется стандартным способом: делением числителя и знаменателя на «эн» в старшей степени. Старшая степень числителя: 1, старшая степень знаменателя: 

Пример 5: Используем признак Лейбница.  1)  Ряд является знакочередующимся. 2)   – члены ряда убывают по модулю. Ряд сходится по признаку Лейбница. Исследуем ряд на абсолютную сходимость: Сравним данный ряд с расходящимся гармоническим рядом  . Используем предельный признак сравнения:  – конечное число, отличное от нуля,  значит, ряд   расходится вместе с гармоническим рядом. Исследуемый ряд сходится только условно.

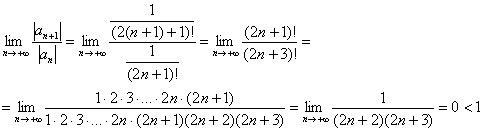Пример 7: Используем признак Лейбница.  1)  Ряд является знакочередующимся. 2)   – члены ряда убывают по модулю. Ряд сходится по признаку Лейбница. Исследуем ряд на абсолютную сходимость: Используем признак Даламбера: Таким образом, ряд  сходится. Исследуемый ряд сходится абсолютно.

Примечание: Возможно, не всем понятно, как разложены факториалы. Это всегда можно установить опытным путём, возьмём и сравним  какие-нибудь соседние члены ряда:   и  , следующий член ряда к предыдущему: 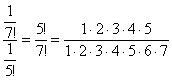    и  , следующий член ряда к предыдущему:   …

Пример 9: Используем признак Лейбница.  1)  Ряд является знакочередующимся. 2)  – так как   более высокого порядка роста, чем  Члены ряда убывают по модулю Вывод: Ряд сходится. Исследуем ряд на абсолютную сходимость: Используем признак Даламбера: Таким образом, ряд   – сходится. Исследуемый ряд сходится абсолютно.

Пример 10: Используем признак Лейбница.  1)  Ряд является знакочередующимся. 2)   – члены ряда убывают по модулю. Ряд сходится по признаку Лейбница. Исследуем ряд на абсолютную сходимость: Используем интегральный признак.   Подынтегральная функция непрерывна на  . Таким образом, ряд   расходится вместе с соответствующим несобственным интегралом.

Исследуемый ряд сходится только условно.