Хід заняття

І. Дайте відповіді на запитання:

1) За якою формулою складається рівняння площини, що проходить через точку перпендикулярно до вектора ?

________________________________________________________________

2. Як виглядає рівняння площини, що проходить через точку перпендикулярно до вектора ?

________________________________________________________________________________________________________________________________

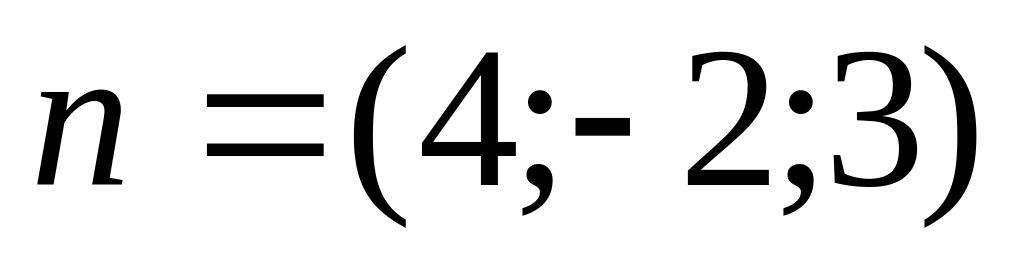3) За якою формулою складається рівняння площини, що проходить через три задані точки?

________________________________________________________________

4) Як виглядає рівняння площини, що проходить через точки , і ?

________________________________________________________________

________________________________________________________________________________________________________________________________________________________________________________________________

5) Як відносно системи координат розташовані площини?

А) ________________________________________________

Б) ________________________________________________

В) _______________________________________________

Г) _______________________________________________

6) За якою формулою складається загальне рівняння прямої у просторі?

________________________________________________________________

7) За якою формулою складається параметричне рівняння прямої у просторі?

________________________________________________________________

8) За якою формулою складається канонічне рівняння прямої у просторі?

________________________________________________________________

9) Як виглядає параметричне і канонічне рівняння прямої, що проходить через точку паралельно до вектора ?

________________________________________________________________

________________________________________________________________

10) Як виглядає загальне рівняння прямої ?

________________________________________________________________

________________________________________________________________

________________________________________________________________

11) За якою формулою складається рівняння прямої, що проходить через точки і ?

________________________________________________________________

12) Як виглядає рівняння прямої, що проходить через точки і ?

________________________________________________________________

________________________________________________________________

Дано дві прямі : і :

13) За якою формулою обчислюється кут між прямими і ?

________________________________________________________________

14) Як виглядає умова паралельності прямих і ?

________________________________________________________________

15) Як виглядає умова перпендикулярності прямих і ?

________________________________________________________________

16) При виконанні якої умови прямі і будуть лежати в одній площині?

________________________________________________________________

17) Як виглядає умова мимобіжності прямих і ?

________________________________________________________________

ІІ. Виконайте завдання:

Завдання 1

Приведіть рівняння прямої до канонічного виду.

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

________________________________________________________________________________________________________________________________

Завдання 2

Складіть рівняння прямої, що проходить через точку

А) паралельно до прямої

________________________________________________________________

Б) перпендикулярно до площини

________________________________________________________________

Завдання 3

Через точки і проведено пряму. Знайдіть точки перетину цієї прямої з координатними площинами.

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Завдання 4

Знайдіть кут між прямими:

А) і

________________________________________________________________________________________________________________________________

Б) і

________________________________________________________________

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Завдання 5

При якому значенні параметра прямі і будуть:

А) паралельні

________________________________________________________________________________________________________________________________

Б) перпендикулярні

________________________________________________________________________________________________________________________________

Завдання 6

З’ясуйте взаємне розташування прямих і

________________________________________________________________

________________________________________________________________

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

ІІІ. Виконайте завдання самостійно

Варіант _______

№ Завдання	1	2	3
Відповідь
Відмітка про виконання

Практичне заняття № 11 до змісту

Тема: Обчислення границь

Мета: навчитися обчислювати границі функцій в точці та на нескінченності, усувати невизначеності типа ; ; ;