8.5. Переходные процессы при некорректных коммутациях

Случаи, когда в цепи скачкообразно изменяется активное сопротивление, были подробно исследованы в предыдущих параграфах. При расчете переходных процессов при мгновенных изменениях индуктивностей или емкостей нужно учитывать особенности определения постоянных интегрирования. В этом случае постоянные интегрирования, как отмечалось ранее (п. 8.1.4), находят из условия неизменности потокосцеплений в замкнутом контуре и сохранения зарядов на емкостях, т.е.

, .

Особенности расчета в данном случае рассмотрим на примерах.

Пример 8.9

Цепь (рис. 8.35) подключена к источнику постоянного напряжения U₀. Параметры элементов цепи: R₁; R₂; C₁; C₂. Рассчитать переходный процесс в цепи.

Решение 1. В установившемся режиме до коммутации все токи и напряжения равны нулю. 2. Для установившегося режима после коммутации конденсаторы соответствуют разрывам цепи. Поэтому:

.

3. В рассматриваемом примере невозможно использовать закон коммутации для конденсатора в виде (8.4). До коммутации напряжения на конденсаторах равнялись нулю. В первый момент после замыкания ключа сумма напряжений на конденсаторах должна быть равной напряжению источника . Поэтому необходимо использовать закон постоянства зарядов (8.3):

или

.

Поскольку

и ,

то получим систему уравнений:

Решение этой системы имеет вид

 .

4. Характеристическое уравнение получим, исходя из системы уравнений, описывающих переходный режим:

   .

Используя соотношения , , преобразуем систему:

; ;

.

Тогда характеристическое уравнение получим в виде

, откуда .

5. Напряжение на первом конденсаторе ищем в виде суммы свободной и принужденной составляющих

,

где – электромагнитная постоянная времени.

Постоянную интегрирования определяем из начальных условий:

; .

Таким образом, окончательный вид временной зависимости напряжения на первом конденсаторе:

.

6. Напряжение на втором конденсаторе вычислим, исходя из второго закона Кирхгофа

.

Токи в сопротивлениях определим из уравнений по закону Ома:

;

.

Токи в конденсаторах из дифференциальных соотношений:

,

.

Когда токи в сопротивлениях и сравняются и прекратится зарядка конденсаторов, наступит установившийся режим.

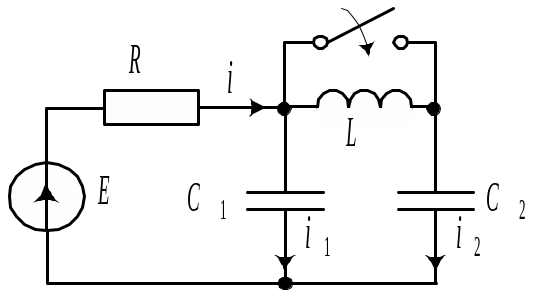
Пример 8.10

Цепь (рис. 8.36) подключена к источнику постоянного напряжения. Параметры элементов цепи: U0=100 В; R1=R2=R=10 Ом; L1=10 мГн; L2=30 мГн. Рассчитать переходный режим. Решение 1. В установившемся режиме до коммутации напряже-

ния на катушках равны нулю. Токи в ветвях в этом режиме:

A, .

2. В установившемся режиме после коммутации ток

A.

3. Используя закон коммутации (8.1) для замкнутого контура:

,

получаем:

; ;

 .

Таким образом, с учетом выражение закона коммутации получаем в виде

, откуда A.

4. Дифференциальное уравнение, описывающее процессы в рассматриваемой схеме после отключения ключа:

.

Из этого уравнения получим характеристическое уравнение для переходного процесса:

откуда .

5. Решение дифференциального уравнения (п.4) находим как сумму свободной и принужденной составляющих:

A.

Постоянную интегрирования определим по начальному значению тока после коммутации :

; A.

Тогда закон изменения тока в цепи после коммутации получим в виде

А.

Из полученного решения легко найти энергию, выделяемую в контакте при замыкании цепи: , где

.

Энергия, теряемая в контакте в момент коммутации

Дж.

Пример 8.11

Рассчитать переходный процесс в цепи, показанной на рис. 8.37. Параметры элементов цепи: А; Ом; Гн, Гн.

Решение В установившемся режиме до коммутации токи на катушках равны нулю. 2. В установившемся режиме после коммутации напряжения на катушках равны нулю, а токи:

А; А.

3. В цепи наблюдается ситуация, рассмотренная в предыдущем примере. Цепь не может в первый момент воспринять ток источника , так как . Но если пренебречь временем горения дуги, то токи к моменту скачком изменятся до начальных значений и .

Независимые начальные условия определяются из принципа непрерывности потокосцеплений, т.е. алгебраическая сумма потокосцеплений в замкнутом контуре в предположении мгновенной коммутации не может измениться скачком . Для заданной схемы:

; .

Таким образом, токи в момент времени :

А; A.

4. Уравнения по законам Кирхгофа:

Эту систему преобразуем к одному дифференциальному уравнению для свободных составляющих:

.

Характеристическое уравнение для переходного процесса имеет вид

, откуда .

5. Токи в цепи ищем в виде суммы свободной и принужденной составляющих:

; .

Постоянные интегрирования получим, используя начальные условия, рассчитанные в п.3:

A;

A.

Тогда искомые решения для токов:

А, А.

Графики токов показаны на рис. 8.38.

Пример 8.12

В цепи (рис. 8.39) действует источник синусоидальной э.д.с. В. Рассчитать переходный режим в цепи, если параметры элементов цепи: ; ; н.

Решение

1. В установившемся режиме до коммутации используем символический метод расчета. Комплекс действующего значения э.д.с. В. Комплексные сопротивления ветвей:

;

Ом.

Таким образом, во второй ветви наблюдается резонанс напряжений, поэтому и . Комплексы тока и напряжения на конденсаторе:

A; B.

Мгновенные значения тока во второй ветви и напряжений на конденсаторах:

В.

В момент коммутации: В.

2. В новом установившемся режиме Ом. Комплексы действующих значений тока и напряжений:

А; В.

Мгновенные значения принужденных составляющих тока и напряжений:

А; В.

3. Идеализация схемы приводит к скачкообразному изменению напряжения . До коммутации . Когда контакты в момент подойдут достаточно близко друг к другу, разность этих напряжений пробивает воздушный промежуток, и за время горения искры напряжения на конденсаторах к моменту выравниваются.

Начальные условия определяются из принципа непрерывности суммарного заряда. Алгебраическая сумма зарядов емкостей, подключенных к узлу, в предположении мгновенной коммутации не может измениться скачком .