8.4.5. Расчет переходного процесса в цепи с двумя реактивными элементами

Пример 8.7

Цепь (рис 8.30) подключена к источнику постоянного напряжения . Параметры элементов цепи: ; ; Гн. Рассчитать токи и напряжения в переходном режиме.

Решение 1. Установившийся режим до коммутации и независимые начальные условия     . 2. Установившийся режим после коммутации или принужденные составляющие:

   .

3. Характеристическое уравнение получим, заменяя на в комплексном входном сопротивлении цепи и приравнивая его к нулю:

;

.

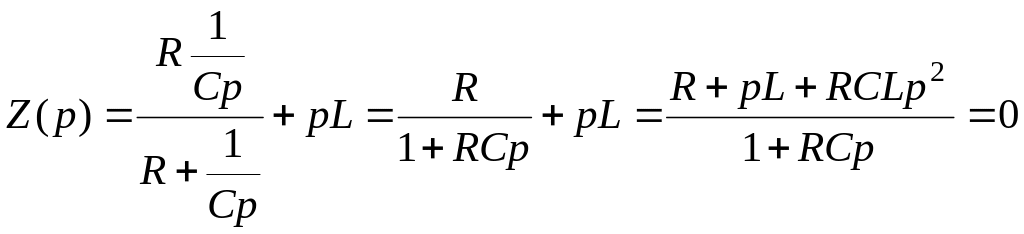Таким образом, характеристическое уравнение имеет вид

.

Корни характеристического уравнения:

4. Полное решение для тока при различных действительных корнях имеет вид

.

Используя второй закон Кирхгофа и уравнения элементов, получим общие выражения для напряжений:

;

.

Постоянные интегрирования определим из алгебраической системы уравнений, полученной в результате подстановки в общие выражения для и независимых начальных условий

; ; .

5. Ток и напряжение записываем на основании полученных общих решений с учетом найденных постоянных интегрирования

 .

Остальные величины определяем по законам Кирхгофа и уравнениям элементов:





a)		б)
Рис. 8.31

.

Временные зависимости токов и напряжений показаны на рис. 8.31.

Пример 8.8

Цепь (рис. 8.32) подключена к источнику синусоидального напряжения . Параметры элементов цепи:

, , . Найти закон изменения напряжения на конденсаторе, если до коммутации . Решение 1. Расчет электрической цепи в установившемся режиме до коммута-

ции выполним по схеме, показанной на рис. 8.33, символическим методом. Комплекс действующего значения приложенного напряжения . По закону Ома найдем ток

.

Мгновенное значение тока до коммутации . Таким образом, в момент коммутации ток в катушке и напряжение на конденсаторе , так как в момент замыкания ключа конденсатор не был заряжен.

2. Расчет установившегося режима после коммутации выполним по схеме, показанной на рис. 8.34, символическим методом. Комплекс действующего значения приложенного напряжения . Расчет напряжения на конденсаторе выполним для комплексов действующих значений:

;

; .

Таким образом, мгновенное значение принужденной составляющей напряжения на конденсаторе

.

3. Входное сопротивление цепи осталось тем же, что и в примере 8.7. Следовательно, не изменилось и характеристическое уравнение:

,

или, подставляя значения параметров цепи . Откуда

.

4. Для определения зависимых начальных условий составим систему уравнений Кирхгофа в момент времени :

С учетом законов коммутации и система имеет решение:

; .

5. Напряжение на конденсаторе может быть записано как сумма принужденной и свободной составляющих:

.

Для нахождения постоянных интегрирования и вычислим так же производную напряжения

При ; . Таким образом, получаем систему уравнений

Решение этой системы: В, В.

Окончательно закон изменения напряжения на конденсаторе имеет вид

.