1.3. Контрольные вопросы

1. Перечислите основные подразделы библиотеки Simulink и блоки, из которых может быть собрана модель линейной динамической системы.

2. Перечислите основные блоки, предназначенные для моделирования источников сигналов и блоки, предназначенные для наблюдения за выходными сигналами системы.

3. Какие элементарные блоки требуются для получения переходной характеристики системы, состоящей из последовательно включенных передаточной функции и интегратора?

4. Какие элементарные блоки требуются для получения переходной характеристики системы, состоящей из параллельно включенных передаточной функции и интегратора? Какие параметры блоков, установленные по умолчанию, следует изменить?

5. Какие элементарные блоки требуются для получения переходной характеристики системы, состоящей из передаточной функции в прямой цепи и усилительного звена в отрицательной обратной связи? Какие параметры блоков, установленные по умолчанию, следует изменить?

6. Для каких целей может быть использован блок мультиплексирования сигналов Mux?

7. В каких случаях следует применять объединение групп элементарных блоков в подсистемы?

8. Перечислите преимущества применения пакета Simulink при изучении теории автоматического управления.

Лабораторная работа 2 математические модели и типовые звенья линейных систем управления

Цель работы: изучение основных математических моделей во временной и комплексной областях отдельных звеньев и их соединений; получение аналитических выражений для амплитудно-фазовых и логарифмических характеристик; моделирование типовых звеньев и получение экспериментальных моделей.

2.1. Основные сведения

Моделью объекта, регулятора или системы управления называется математическое преобразование, позволяющее по известному входному воздействию определять или вычислять выходную переменную. Математические модели (ММ) или описания линейных непрерывных систем, их элементов и устройств разделяют на ММ во временной (или области действительного переменного)и комплексной областях. В первом случае – это дифференциальные уравнения, весовая и переходная функции, во втором – передаточные функции (ПФ) и частотные характеристики (ЧХ).

Основной ММ во временной области является обыкновенное дифференциальное уравнение (ОДУ) вида:

(2.1)

и при описании непрерывных систем должно выполняться требование n ≥ m или условие физической реализуемости.

ОДУ будет ММ, так как по известному входному сигналу x(t) и заданных начальных условиях

(2.2)

можно аналитически или численно решить уравнение (2.1) и определить выходную переменную y(t).

Импульсная или весовая функция w(t), получается на выходе системы, т.е. y(t)=w(t), если на ее вход подать дельта-функцию

(2.3)

а переходная функция h(t) получается, если x(t)=1(t), где

(2.4)

Собственно ММ является только w(t) и выходная переменная y(t) определяется на ее основе с помощью интеграла свертки вида:

(2.5)

Временные функции w(t) и h(t) связаны следующими эквивалентными соотношениями:

.

В комплексной области к ММ относится одностороннее непрерывное преобразование Лапласа (ОНПЛ) вида:

, (2.6)

где x(t) называют оригиналом, а X(s) – его изображением.

Аналогичное преобразование можно записать и для сигнала y(t). Широкое применение ОНПЛ связано с алгебраизацией дифференциальных уравнений и получением простых ММ.

При нулевых начальных условиях для сигнала x(t) и его производных справедливы следующие выражения:

Аналогично соотношения записываются и для переменных , поэтому, применяя к уравнению (2.1) ОНПЛ, получим:

(2.7)

Введем полиномы и вида:

тогда вместо выражения (2.7) можно записать:

(2.8)

Передаточной функцией по определению называется отношение преобразованных по Лапласу при нулевых начальных условиях выходного сигнала к входному

(2.9)

т.е. ПФ является ММ, так как по известному изображению входного сигнала X(s) можно достаточно просто определить Y(s) в виде следующего произведения:

(2.10)

Учитывая выражение (2.8) и полиномы , передаточную функцию записывают в дробно-рациональной форме

(2.11)

а также через нули s_j и полюса s_i передаточной функции следующим образом:

(2.12)

где нули s_j являются корнями уравнения числителя , а полюса s_i – знаменателя .

Аппарат ПФ позволяет ОДУ также записывать в операторной форме. Введем для производных, например, сигнала y(t) операторные обозначения:

тогда ОДУ запишется в виде:

(2.13)

или

(2.14)

где

Тогда по аналогии с выражением (2.10) ОДУ можно представить в операторной форме

, (2.15)

поэтому в силу схожести формул (2.15) и (2.10) преобразование W(p) называют передаточной функцией в операторной форме.

С помощью аппарата ПФ можно осуществить структурные преобразования при различных соединениях звеньев (рис. 2.1).

а

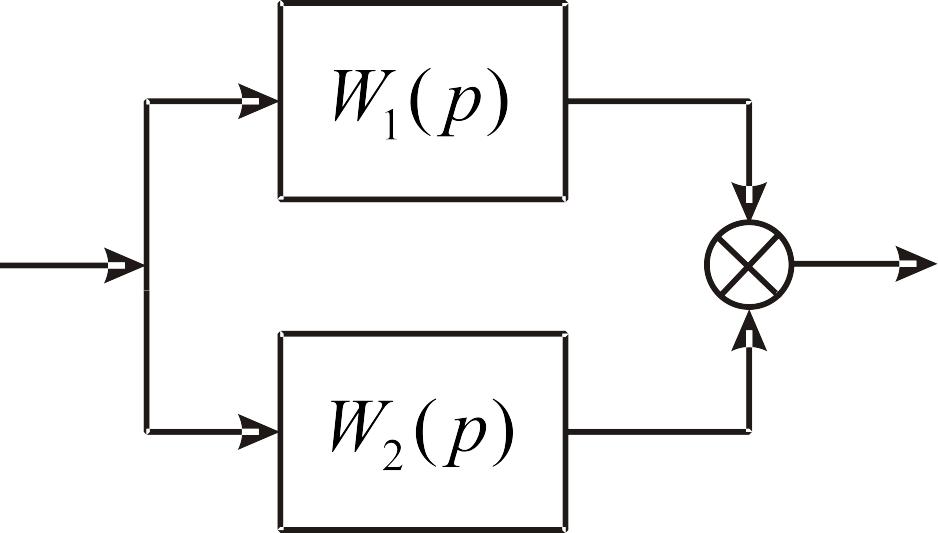
б в     

Рис. 2.1 Основные соединения звеньев в системах

При последовательном соединении (рис. 2.1, а)

, (2.16)

параллельном согласном (рис. 2.1, б)

, (2.17)

параллельном встречном (рис. 2.1, в)

. (2.18)

Передаточные функции как ММ линейных систем достаточно сложно получить экспериментально, поэтому используют одностороннее непрерывное преобразование Фурье (ОНПФ) вида:

, (2.19)

которое является частным случаем ОНПЛ при .

Основная ММ системы определяется следующим образом:

(2.20)

и называется амплитудно-фазовой (частотной) характеристикой или АФХ (АФЧХ) системы.

Для частотных характеристик или спектров выходного и входного сигналов по аналогии с моделью (2.10) можно записать

. (2.21)

АФХ системы является комплексной функцией, поэтому используют две формы. В первом случае

, (2.22)

где называют вещественной частотной характеристикой, а – мнимой.

При изменении частоты геометрическое место точек конца вектора называют годографом АФХ.

Другой формой записи является:

, (2.23)

где – амплитудная; – фазовая частотные характеристики, которые связаны с и следующим образом:

.

На практике строят логарифмические характеристики, когда по оси абсцисс частота изменяется в логарифмическом масштабе. Логарифмическая амплитудная частотная характеристика (ЛАХ) получается из по формуле

(2.24)

и измеряется в децибелах (дБ), а логарифмическая фазовая частотная характеристика (ЛФХ) совпадает с и откладывается в градусах или радианах.

В теории автоматического управления отдельные элементы, блоки или устройства, описываемые одинаковыми математическими моделями принято называть звеньями, которые в свою очередь разделяются на типовые, особые и неустойчивые. К типовым относятся звенья, обладающие условиями устойчивости и минимально-фазовости (все полюса s_i и нули s_j передаточной функции (2.12) имеют отрицательные вещественные части). К простейшим типовым звеньям относят усилительное, интегрирующее и идеальное дифференцирующее.

Усилительное (пропорциональное, статическое) звено описывается уравнением вида

, (2.25)

где k – коэффициент передачи (усиления).

Передаточная функция , такой же вид имеет . Логарифмические характеристики:

. (2.26)

Дифференциальное уравнение для интегрирующего звена имеет вид:

, (2.27)

или в форме, которая дала наименование звену, –

, (2.28)

где k – коэффициент передачи.

Применяя к формуле (2.28) преобразование Лапласа, запишем выражение для передаточной функции:

, (2.29)

при из модели (2.29) получим АФХ:

, (2.30)

и логарифмические характеристики

; (2.31)

, (2.32)

которые приведены на рис. 2.2, а.

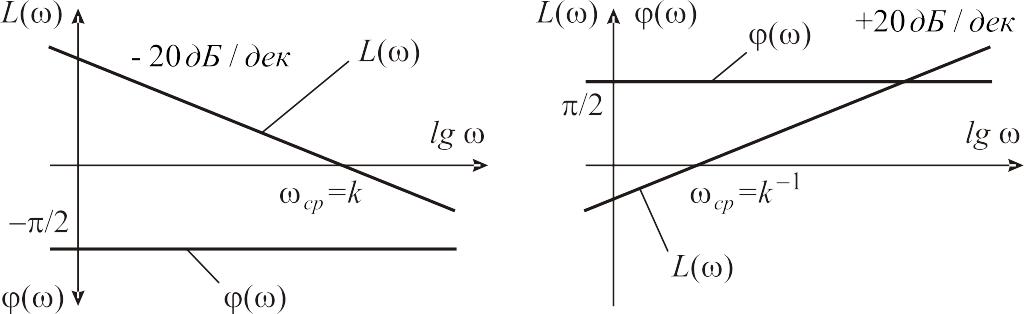
а б Рис. 2.2. Логарифмические частотные характеристики интегрирующего и идеального дифференцирующего звеньев

В соответствии с формулой (2.31) зависимость при логарифмическом масштабе оси частот является прямой линией. При некоторой фиксированной частоте ЛАХ определяется следующим образом:

. (2.33)

Увеличим частоту в десять раз, тогда

(2.34)

или

. (2.35)

Из сравнения выражений (2.33) и (2.35) следует, что при увеличении частоты в десять раз, т.е. на декаду, ЛАХ уменьшится на 20 дБ, поэтому говорят, что характеристика является прямой с наклоном –20дБ/дек, который указывается на графике ЛАХ (см. рис. 2.2, а). Так же можно показать частоту среза , когда выполняется

(2.36)

Подставляя в выражение (2.31) и учитывая равенство (2.36), получим

(2.37)

откуда следует, что .

Звено идеального дифференцирования описывается уравнением

, (2.38)

где k – коэффициент передачи.

Запишем ПФ и АФХ звена

. (2.39)

Логарифмические характеристики будут иметь вид:

; (2.40)

, (2.41)

графики которых приведены на рис. 2.2, б.

По аналогии с выражением (2.31) интегрирующего звена можно на основе формулы (2.40) заключить, что, во-первых, зависимость является прямой линией с наклоном +20дБ/дек и, во-вторых, частота среза .

Используя параллельное встречное соединение интегрирующего и усилительного блоков, можно получить апериодическое звено с ПФ вида

, (2.42)

где k – коэффициент передачи; Т – постоянная времени.

Звено описывается следующим дифференциальным уравнением:

. (2.43)

Подставляя в формулу (2.42), после несложных преобразований получают АФХ:

(2.44)

и логарифмические характеристики –

; (2.45)

. (2.46)

Графики зависимостей для ЛАХ и ЛФХ, построенные по выражениям (2.45) и (2.46), приведены на рис. 2.3, а.

а б Рис. 2.3. Логарифмические характеристики апериодического звена

Реальная ЛАХ может быть аппроксимирована кусочно-линейной зависимостью или асимптотической . Для этого область изменения разделяют на два диапазона. При из формулы (2.45) получается низкочастотная асимптота:

, (2.47)

при – высокочастотная –

. (2.48)

Если сравнить выражение (2.48) с формулой (2.31) интегрирующего звена, то асимптота представляет собой прямую с наклоном –20дБ/дек, а асимптота не зависят от , поэтому она параллельна оси частот или имеет наклон 0дБ/дек (см. рис. 2.3, а).

При частоте сопряжения

(2.49)

обе асимптоты совпадают, поэтому выражение (2.49) определяет частоту сопряжения и ЛФХ равна . Вид асимптотической ЛАХ апериодического звена приведен на рис. 2.3, б.

Рассмотрим математические модели для форсирующего звена. Дифференциальное уравнение имеет вид

. (2.50)

Передаточную функцию после применения к модели (2.50) преобразования Лапласа записывают следующим образом:

, (2.51)

а на основе выражения (2.51) частотные характеристики:

; (2.52)

; (2.53)

. (2.54)

К типовым относят еще ряд звеньев. Приведем ОДУ и ПФ для некоторых звеньев первого порядка:

для звена реального дифференцирования –

; (2.55)

; (2.56)

для изодромного звена –

; (2.57)

. (2.58)

Из звеньев второго порядка приведем основные ММ для инерционно-интегрирующего звена:

; (2.59)

. (2.60)

Колебательное звено также относится к звеньям второго порядка, описывается дифференциальным уравнением:

, (2.61)

где k – коэффициент передачи; Т – постоянная времени; – степень затухания и имеет передаточную функцию

. (2.62)

Тип звеньев зависит от степени затухания , так, если , то модели (2.61) и (2.62) описывают консервативное звено, если , то – инерционное звено второго порядка. Собственно колебательное звено будет при .

Заменяя в выражении (2.62) величину на , получим АФХ колебательного звена

. (2.63)

и логарифмические характеристики

. (2.64)

. (2.65)

Как звено второго порядка колебательное имеет наклон высокочастотной асимптоты –40дБ/дек, а логарифмическая фазовая характеристика изменяется от нуля до , а на частоте сопряжения значение .