Основные положения

Р

Система работоспособна до тех пор, пока число исправных элементов не меньше n, т.е. пока . Схема функционирования такой системы представлена на рис.2, где двойными стрелками показаны перемещения исправных элементов, а одинарными - отказавших элементов.

На рис. 2 обозначены интенсивности потоков отказавших и восстановленных элементов.

ассматривается система, состоящая из n основных (рабочих) элементов и m резервных, однотипных с основными. При отказе основной элемент мгновенно заменяется резервным, при этом переключатель (т.е. устройство, осуществляющее обнаружение отказавшего элемента и подключение резервного) считается абсолютно надежным. Отказавший элемент направляется на восстановление, которое начинается сразу же с момента его отказа. Одновременно восстанавливаться может не более S элементов. Если число k отказавших элементов превышает S, то (k-S) элементов ожидают своей очереди.

Здесь - интенсивность отказа элемента в рабочем (загруженном) режиме; - в режиме резервирования, - интенсивность восстановления. При этом под интенсивностью понимается число отказов (восстановлений) в единицу времени.

Нетрудно убедиться, что если систему восстановления рассматривать как систему массового обслуживания (СМО), то на рис. 1 изображена схема замкнутой СМО (с ограниченным входящим потоком требований).

В зависимости от того, какому закону распределения подчиняются случайные времена

безотказной работы основных и резервных элементов и их восстановления, эта СМО может принадлежать классу марковских или немарковских и соответственно исследоваться аналитически либо путем имитационного моделирования.

Если предположить, что все вышеперечисленные случайные величины подчинены экспоненциальному закону с параметрами соответственно, то вероятности того, что в момент t на восстановлении находится ровно k элементов, определяются из уравнений:

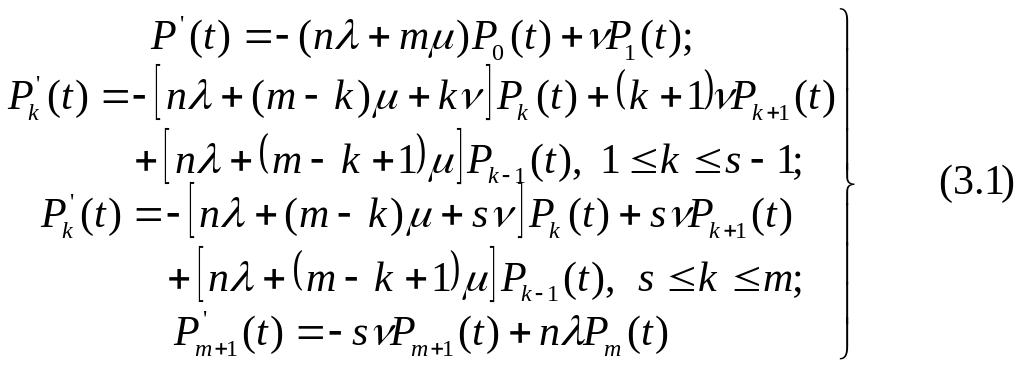
Эти уравнения написаны в предположении, что когда в работоспособном состоянии окажется меньше n элементов, то в системе наступает отказ и ее функционирование прекращается до тех пор, пока число исправных элементов за счет восстановления не станет снова не меньше n. При этом подразумевается также, что s<m (т.е. возможна очередь на восстановление), и если система в целом неисправна, то ее элементы уже не отказывают.

Так как множество состояний системы конечно, то при достаточно длительном функционировании ее можно рассматривать как находящуюся в режиме статистического равновесия (P_k(t)=P_k).В этом случае система уравнений (3.1) сводится к системе алгебраических уравнений:

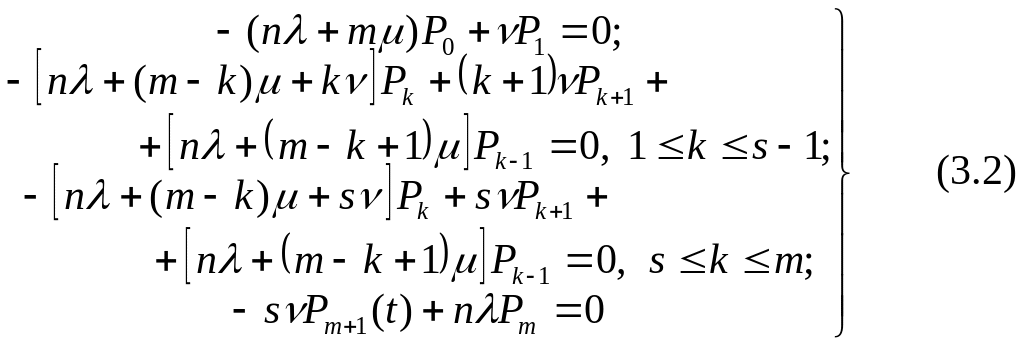
Решение системы (3.2) имеет вид (1):

Получив решения системы (3.1) (см. работу №1) или произведя вычисления по формулам (3.3), можно на базе распределения P_k(t) или P_k находить показатели надежности системы как в нестационарном (начальном) режиме ее функционирования, так и в стационарном, т.е. в режиме длительного функционирования.

Решения, полученные на основе уравнений (3.1) или (3.2) и (3.3), относятся, как уже указывалось, к случаю, когда времена безотказной работы основных и резервных элементов, а также время их восстановления подчинены экспоненциальному распределению. Если это условие нарушено, процесс K(t) перестает быть марковским, и для изучения надежности системы в таком (произвольном) случае используется метод имитационного моделирования СМО (см. работу № 2).

Инструкцию по работе с программой и варианты заданий получить у преподавателя.