Решение.
1-й вариант. Вычисления по формулам с помощью подручных вычислительных средств проводим по формуле (15):
i э = (1 + j / m)m -1= (1+ 0,16 /4)4 - 1 = 0,170, или 17,0%.
2-й вариант. Расчет эффективной ставки выполним в Excel по формуле (15), результаты расчета представлены на рис. 15.
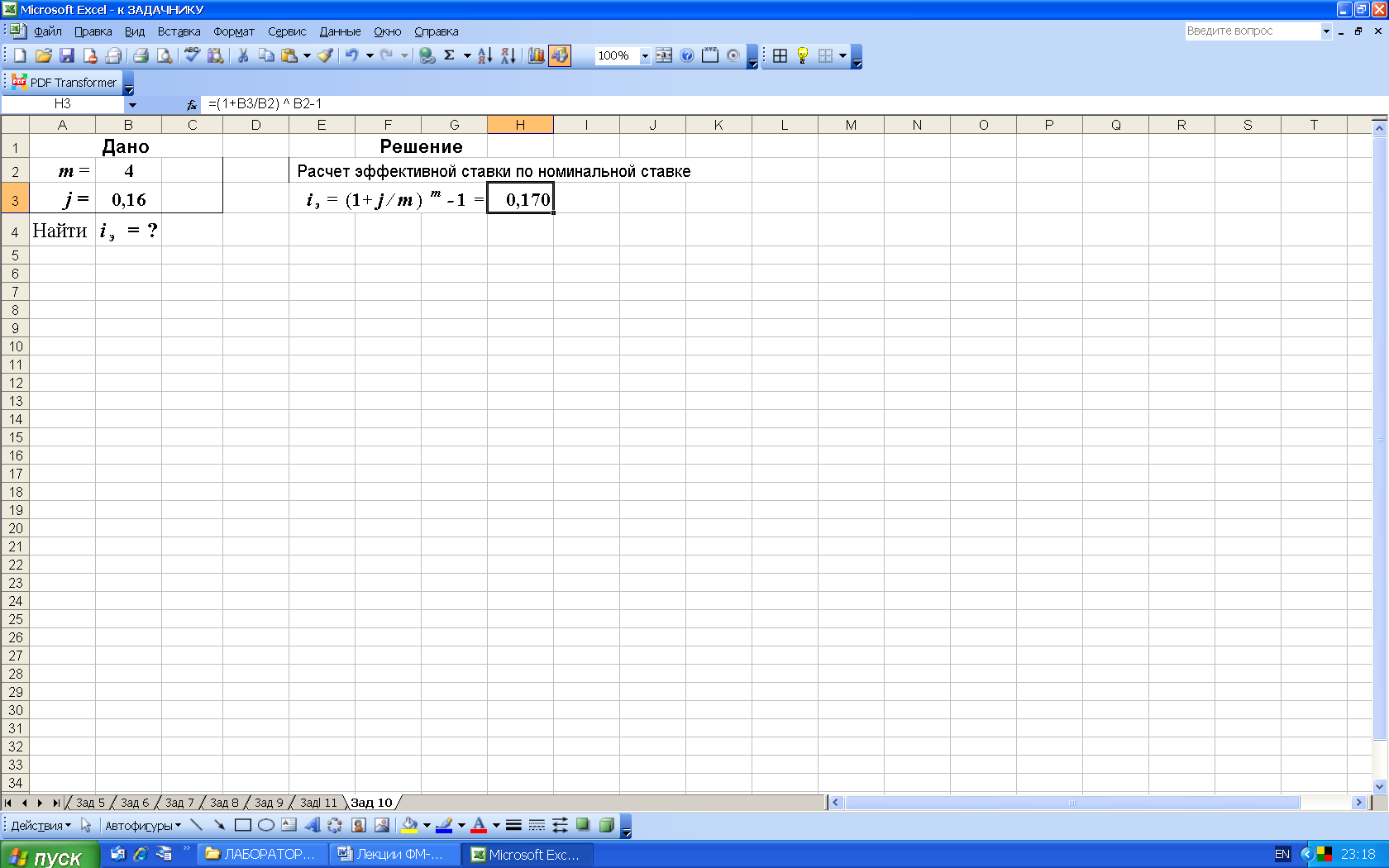
Рис. 15. Результаты расчета эффективной ставки в среде Excel. В ячейку H3 введена формула =(1+B3/B2) ^ B2-1
3-й вариант. Расчет эффективной ставки выполним в среде Excel с использованием функции ЭФФЕКТ (из категории Финансовые). Данная функция возвращает эффективную (фактическую) процентную ставку, при заданной номинальной процентной ставке и количестве периодов, за которые начисляются сложные проценты, рис.16.
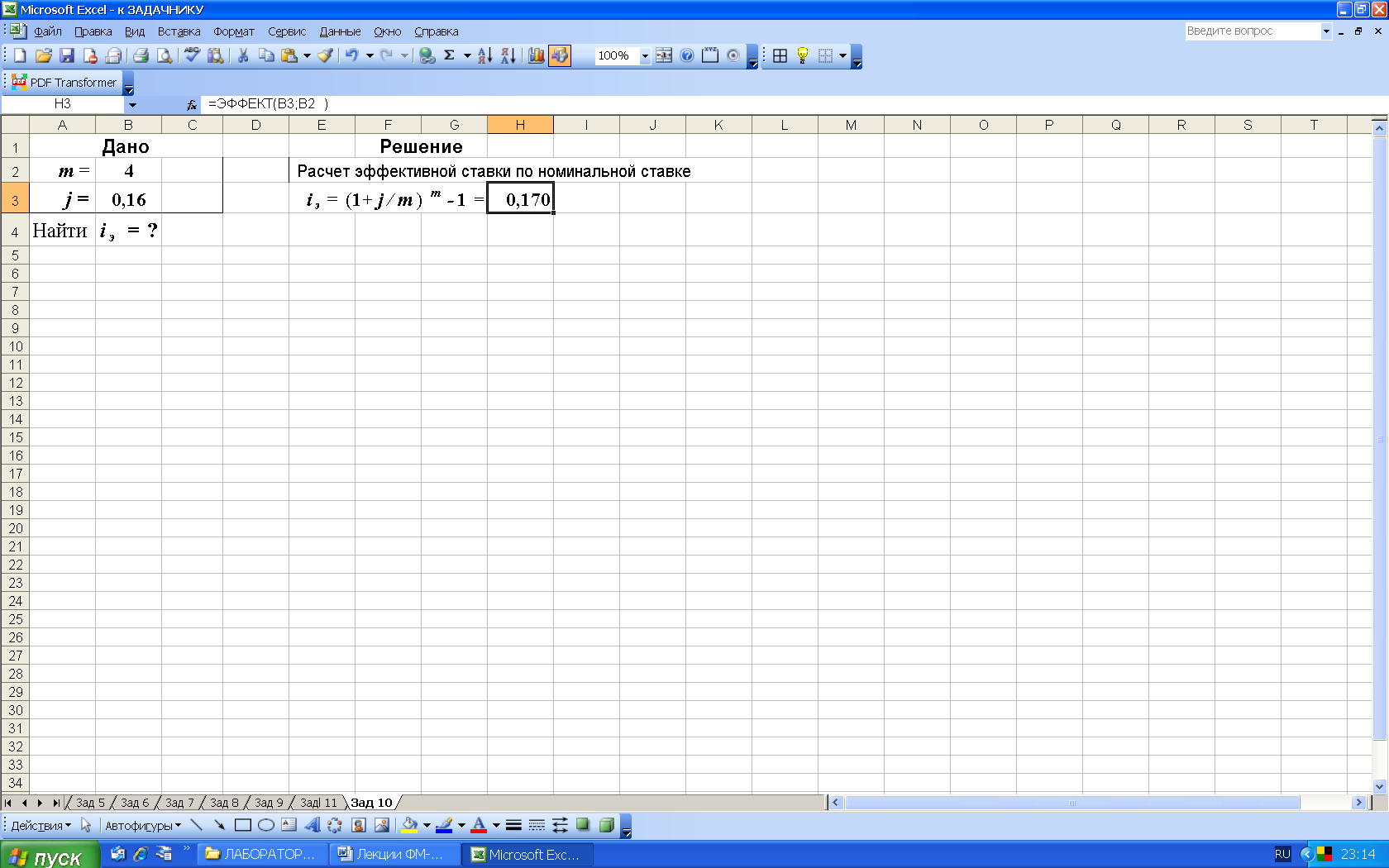
а)
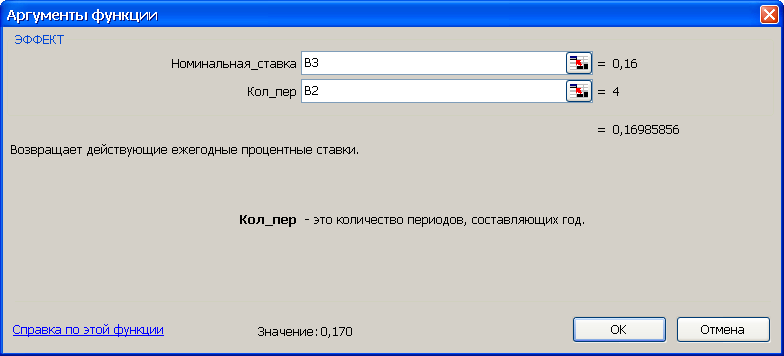
б)
Рис. 16. Результаты расчета эффективной ставки (рис. а) и вид диалогового окна ЭФФЕКТ с введенными данными (рис. б). В ячейку H3 введена формула =ЭФФЕКТ(B3;B2)
Синтаксис функции ЭФФЕКТ (номинальная_ставка;кол_периодов). Аргументы функции:
номинальная_ставка – значение номинальной процентной ставки,
кол_периодов – количество периодов начисления.
Обратная зависимость между номинальной и эффективной ставкой выражена следующей формулой:
j = m [(1+ iэ )1/m-1]. ( 16)
Пример 10. Определить, какой должна быть номинальная ставка при ежеквартальном начислении процентов, чтобы обеспечить эффективную ставку в 12% годовых.
Известно:
iэ = 0,12 или 12% .
Найти j = ?
Решение.
1-й вариант. Вычисления по формулам с помощью подручных вычислительных средств произведем по формуле (16):
j = m [(1+ iэ )1/m-1] = 4*[ (1+0,12) (1/4) - 1 ] = 0,11495, или 11,495%.
2-й вариант. Для выполнения расчетов по формулам в среде Excel воспользуемся математической функцией СТЕПЕНЬ, рис. 17.
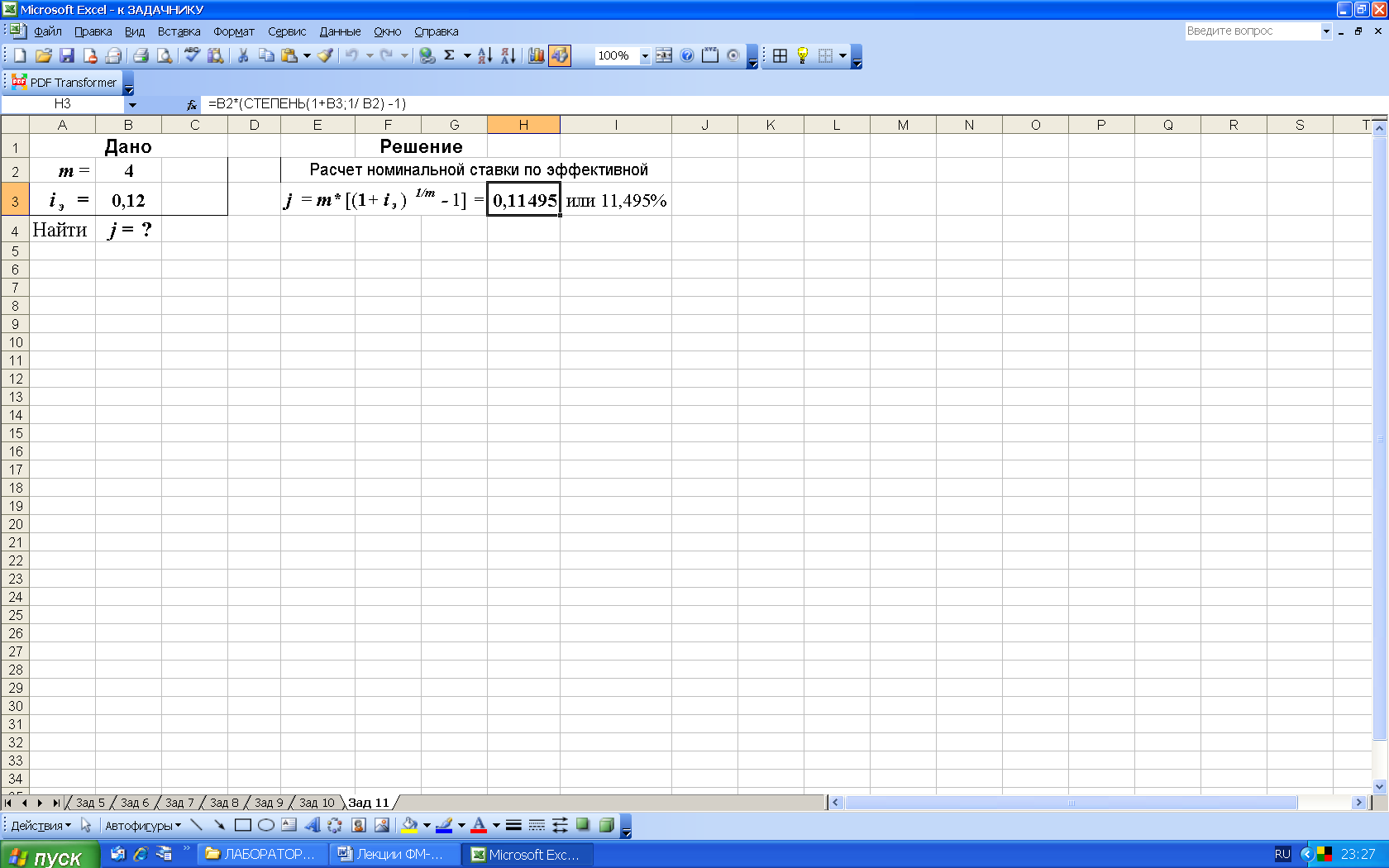
Рис. 17. Результаты расчета эффективной ставки в среде Excel. В ячейку H3 введена формула =B2*(СТЕПЕНЬ(1+B3;1/B2)-1)
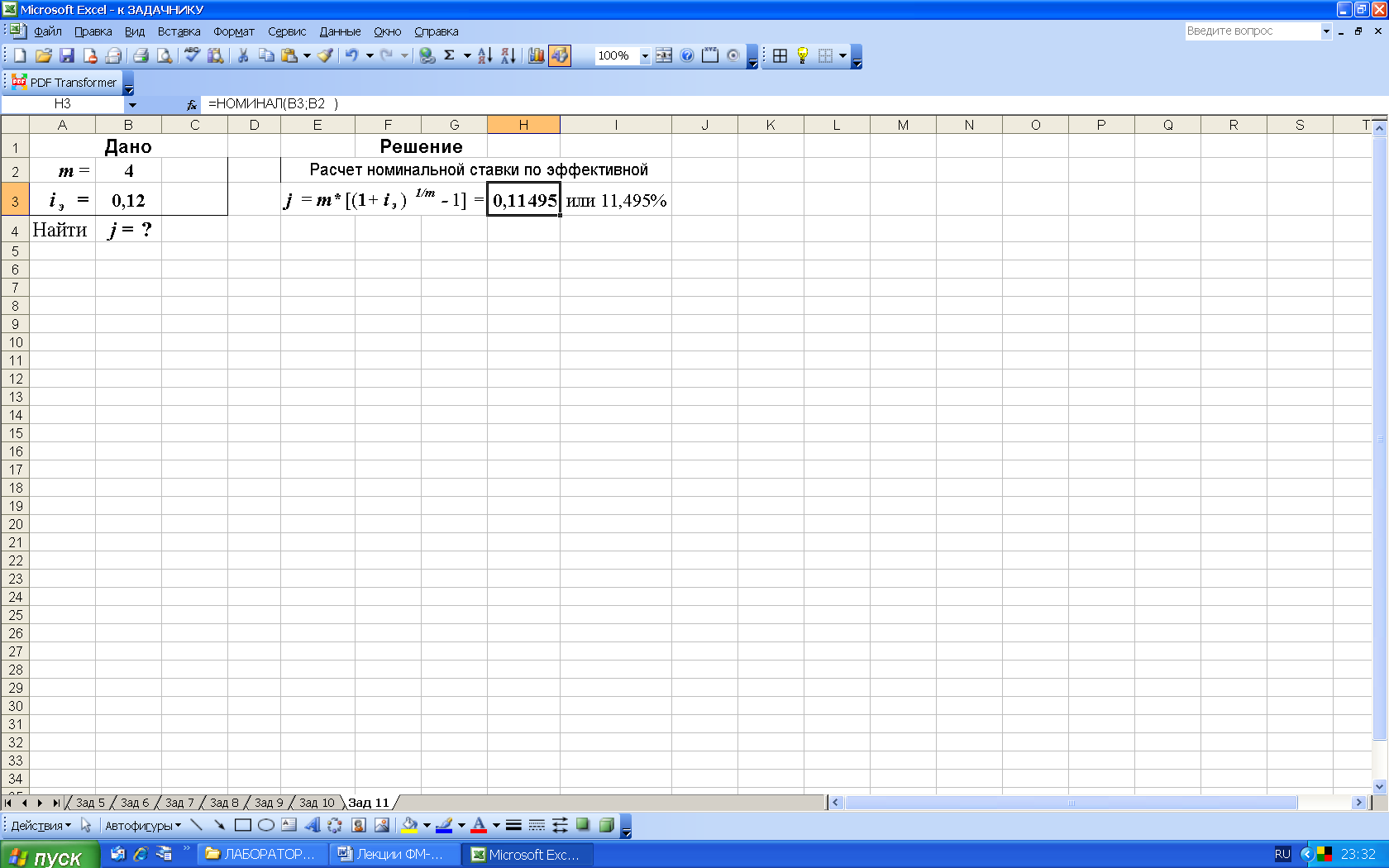
3-й вариант. Для выполнения расчетов номинальной ставки воспользуемся функцией НОМИНАЛ (из категории Финансовые). Данная функция возвращает номинальную годичную ставку при заданной эффективной ставке и числе периодов, за которые начисляются проценты. Результат расчета приведен на 18.
а)
б)
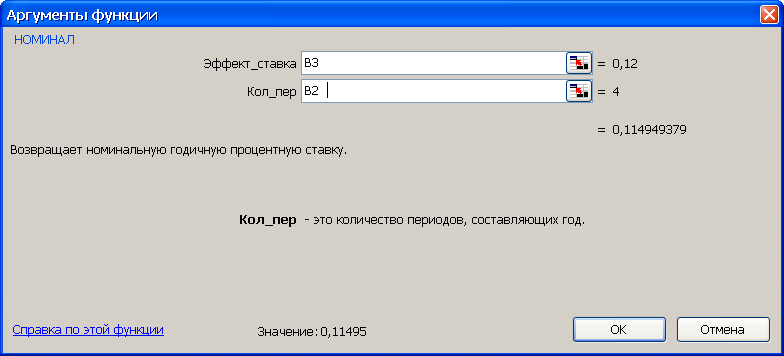
Рис. 18. Результаты расчета номинальной ставки (рис. а) и вид диалогового окна НОМИНАЛ с введенными данными (рис. б). В ячейку H3 введена формула =НОМИНАЛ(B3;B2)
Синтаксис функции НОМИНАЛ (эффект_ставка;кол_пер). Аргументы функции:
эффект_ставка – значение эффективной процентной ставки,
кол_пер – количество периодов начисления.
2.4.Учет (дисконтирование) по сложной ставке процентов
Математический учет. В этом случае решается задача обратная наращению по сложным процентам. Запишем формулу S = P(1 + i )n для наращения по сложной ставке с начислением процентов один раз в год и перепишем ее относительно Р:
P = S/(1 + i ) n = Sν n , (17)
где дробь ν n = 1/(1 + i ) n (18)
является учетным, или дисконтным множителем.
Пример 11. Через 5 лет предприятию будет выплачена сумма 1 000 000 руб. Определить его современную стоимость при условии, что применяется ставка сложных процентов в 14% годовых.
Известно:
n = 5 лет,
S = 1 000 000 руб.,
i = 0,14 или 14% .
Найти P = ?