1. Теорема о конечном перемещении твердого тела, имеющего одну неподвижную точку

Тело, имеющее одну неподвижную точку, из одного положения в любое другое можно перевести одним поворотом вокруг оси, проходя щей через неподвижную точку. Эту ось называют осью конечного вращения.

2. Мгновенная ось вращения. Аксоиды

Ось, вокруг которой следует вращать тело, имеющее одну неподвижную точку, для перевода его из одного положения в другое, бесконечно близкое первому, называют мгновенной осью вращения (или мгновенной осью) для данного момента времени.

Геометрическое место мгновенных осей относительно неподвижных осей координат, по отношению к которым рассматривается движение тела, называется неподвижным аксоидом.

Геометрическое место мгновенных осей в движущемся теле представляет подвижный аксоид, являющийся также конической поверхностью.

3. Угловая скорость и угловое ускорение при вращении тела вокруг неподвижной точки

В водимая угловая скорость является векторной величиной, направленной в каждый момент времени по соответствующей мгновенной оси, и при использовании правой системы координат вектор угловой скорости направлен по мгновенной оси так, что с направления этого вектора видно вращение тела вокруг мгновенной оси против часовой стрелки. Модуль вектора угловой скорости можно выразить через элементарный угол поворота вокруг мгновенной оси за время :

Рис. 40

.

Вектор угловой скорости можно прикладывать в любой точке мгновенной оси (рис. 40). Вектор углового ускорения является производная по времени от вектора угловой скорости . Таким образом, угловое ускорение

.

4. Скорости точек тела при вращательном движении вокруг неподвижной точки

С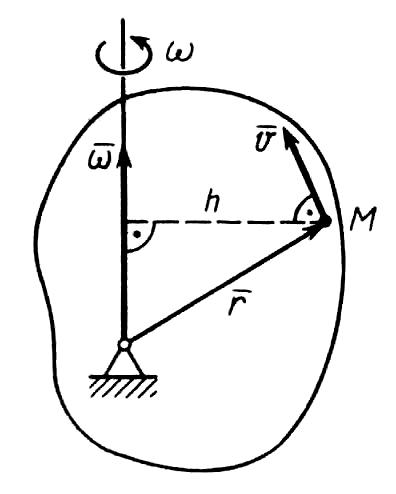 корость какой-либо точки М тела (рис. 41), по векторной формуле Эйлера,

(*)

Модуль скорости

где h-кратчайшее расстояние от рассматриваемой точки до мгновенной оси.

Таким образом, скорости точек тела пропорциональны расстояниям от этих точек до мгновенной оси. Направление скорости какой-либо точки тела перпендикулярно плоскости, в которой находятся векторы и , а следовательно, перпендикулярно отрезку h.

Е

Рис. 41

сли спроецировать правую и левую части (*) на координат­ные оси, то получим формулы Эйлера для проекций скоростей v_x, v_y и v_z:

; ; .

где х, у, z - координаты точек тела, скорости которых опре­деляются.

Если взять точки тела, лежащие на мгновенной оси, то получим следующие уравнения для координат этих точек:

; ; .

Эти уравнения можно представить в виде

( **)

Если х, у, z являются текущими координатами точки мгновенной оси относительно подвижных осей, скрепленных с движущимся телом, а , , проекции угловой скорости тела на эти оси, то формула (**) является уравнением подвижного аксоида.

Если взять подвижную систему координат Oxyz, скреплен­ную с телом, которое вращается вокруг неподвижной точки с угловой скоростью , то для единичных векторов , , , направленных по этим осям координат, как для векторов, модули которых постоянны, имеем:

; ;

Эти формулы называют формулами Пуассона.

5. Ускорения точек тела при вращении вокруг неподвижной точки

Формулу для ускорения какой-либо точки тела М можно получить путем дифференцирования по времени вектора скоро­сти, учитывая, что скорость вычисляют по формуле . Выполняя это дифференцирование, получаем

Так как

, ,

то

(1)

Формулу (1) часто называют формулой Ривальса.

Часть общего ускорения точки

(2)

называют вращательным ускорением, а другую часть

(~) - осестремительным ускорением. Следовательно, формула (1) примет вид

т. е. ускорение точки тела, вращающегося вокруг неподвижной точки, равно векторной сумме вращательного и осестремительного.­

Модуль вращательного ускорения определяют аналогично модулю скорости v :

, (3)

г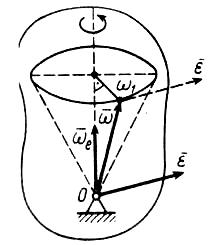 де h₁ – кратчайшее расстояние от точки тела до линии, по которой направлено угловое ускорение (рис. 42).

Формула (3) для получается из (2):

,

где .

Модуль осестремительного ускорения можно получить из формулы (~):

Рис. 42