МО РБ

УО «Полоцкий государственный университет»

Кафедра КиТРЭС

Лабораторная работа № 1 «представление и запись двоичных чисел» Группа 10вс

Выполнил _____________ Лейченок Д.В.

Проверила _____________ Бульбенкова Т.А.

Новополоцк 2012 г.

Цель работы: Изучить правила перевода чисел из одной системы исчисления в другую. Изучить способы кодирования двоичных чисел. Изучить формы представления двоичных чисел, а также способы перевода одной формы записи в другую.

Краткие теоретические сведения

Системой исчисления называют систему приемов и правил, которые позволяют устанавливать взаимно однозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов.

представлением в виде совокупности конечного числа символов.

Любая позиционная система исчисления с основой может быть представлена в виде полинома:

, (1)

где – число в позиционной системе исчисления с основой ;

– коэффициент;

– степень и индекс.

Вес каждого символа определяется его позицией в записи числа.

В двоичной системе исчисления основанием системы является число 2, а коэффициенты могут принимать значения или . Эти двоичные цифры называются битами. В общем виде число в двоичной системе исчисления будет записано как

(2)

1. Правила перевода чисел из одной системы исчисления в другую

1. Преобразование десятичных чисел в двоичные

Пусть имеем целое десятичное число . Преобразовать его в двоичное число – это значит представить в виде

, (1.1)

где – двоичные цифры, равные или .

Цифры двоичного числа можно определить последовательно, начиная с и кончая , следующим образом:

а) делим заданное число на 2. В результате получаем целую часть частного

(1.2)

и остаток .

б) делим число на 2. В результате получаем в частном

(1.3)

и в остатке и т.д.

Процесс деления продолжается до тех пор, пока мы не получим в частном и в остатке . Это означает, что мы определили старший разряд двоичного числа.

Пусть имеем дробное десятичное число < . Требуется определить двоичную дробь

, (1.4)

где – двоичные цифры, равные или .

Цифры двоичного числа можно определить последовательно, начиная с , следующим образом:

а) умножаем заданное число на 2:

(1.5)

Отделяем целую часть числа , равную и дробную часть

(1.6)

б) умножаем на 2:

(1.7)

Целая часть от равна , а дробная часть

(1.8)

используется для дальнейшего преобразования.

Преобразование продолжается до тех пор, пока после очередного умножения на 2 дробная часто не окажется равной нулю (что означает точное преобразование в двоичную дробь) или пока мы не получим достаточное количество двоичных разрядов, удовлетворяющее нас с точки зрения точности преобразования.

Рассмотрим процесс преобразования десятичного числа в соответствующее двоичное (см. рисунок 1).

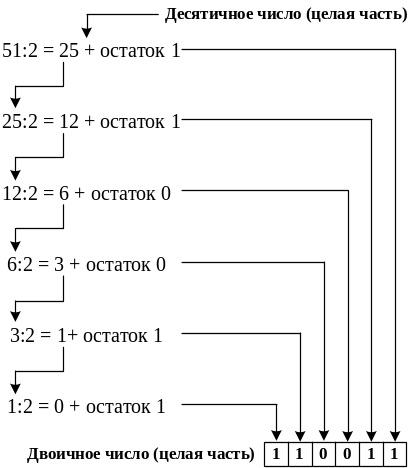
а)

б)

Рисунок 1 – Процесс преобразования десятичного числа в двоичное:

а) целая часть; б) дробная часть

Итак,

2. Преобразование двоичных чисел в десятичные

Для этого надо двоичное число

(1.9)

представить в виде

(1.10)

и непосредственно выполнить все указанные в этой формуле действия.

2. Кодирование двоичных чисел

2.1. Прямой код числа

Простейшим машинным кодом является прямой код , получаемый при кодировании в числе только знаковой информации, причем знак «+» кодируется нулем, а знак «–» – единицей. Поэтому прямой код положительного числа совпадает с его записью, а прямой код отрицательного числа отличается от обычной записи числа знаковым разрядом, в который заносится единица.

2.2. Обратный код числа

Для образования обратного кода отрицательного числа необходимо в знаковом разряде поставить единицу, а все цифровые разряды инвертировать (заменить на , а – на ). Очевидно, что

2.3. Дополнительный код числа

Дополнительный код отрицательного числа образуется из обратного кода путем увеличения на единицу младшего разряда.

Пример:

Число Прямой код Обратный код Дополнительный код

3. Формы представления чисел

1. Представление чисел в форме с фиксированной запятой

Для сокращения длины разрядной сетки и упрощения обработки данных положение запятой может быть зафиксировано схемотехнически. При этом формат машинного представления чисел с фиксированной запятой состоит только из двух структурных компонент: поле знака и поле цифр.

Диапазон представления чисел для этого формата .

В зависимости от размеров целой и дробной частей возможны следующие случаи:

1) Если , , то

2) Если , , то

3) Если , , то

4) Если , , то

Очевидно, что ограничение длины разрядной сетки приводит к ограничению диапазона хранимых чисел и потере точности их представления. Поэтому на практике широко используется и другая форма представления чисел.