13.4. Движение дислокации с порогами

Пороги на дислокациях в зависимости от их высоты подраз­деляют на короткие (элементарные) и длинные (составные). Вы­сота элементарного порога равна вектору Бюргерса пересекающей дислокации. Пороги на рис. 1—4 элементарные.

Если же дислокацию последовательно пересекает ряд дисло­каций, скользящих в одной плоскости, то возникает длинный (со­ставной) порог размером в несколько векторов Бюргерса.

Порог РР' краевой дислокации на рис. 13.1,б имеет краевую ориентацию и лежит в плоскости klтп, являющейся одной из плоскостей скольжения в кристалле. Поэтому порог РР' может скользить вместе со своей краевой дислокацией ЕР, которая сколь­зит в плоскости rstv.

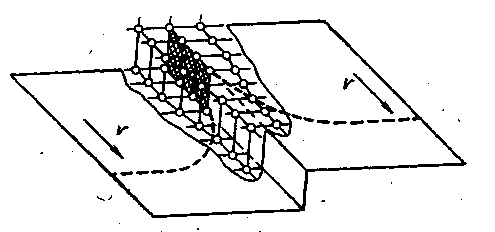
Рис. 13.5 Скользящая винто­вая дислокация с элементар­ным порогом, имеющим краевую ориентацию: v – направления скольжения

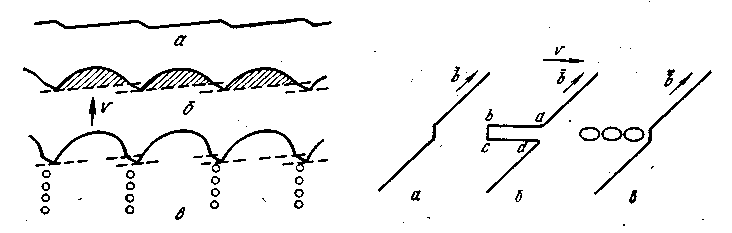
Значительно многообразнее и важнее поведение порогов на винтовых дислокациях. Эти пороги (см, рис. 13.3, б и 13.4,6) имеют краевую ориентацию способны скользить, только вдоль линии винтовой дислокации в направлении вектора Бюргерса, Напри­мер, на рис. 4,5 элементарный порог РР' может скользить только вдоль линии СD. Винтовая же дислокация СD на рис.4 скользит справа налево. Ее порог РР' в этом направлении может перемещаться нормальным способом только переползанием — медленной диффузионной достройкой экстраплоскости, находя­щейся справа от порога РР'.

Быстро скользя, справа налево, дислокация как бы протаски­вает за собой порог РР', оставляя на его пути (заштрихован на рис. 13.4,б) дорожку вакансий. Протаскивание элементарного порога на одно межатомное расстояние влево означает образова­ние позади него вакансии. Рис. 13.5 более наглядно иллюстрирует образование дорожки из вакансий (пустоты перед заштрихован­ной экстраплоскостью) при протаскивании порога. Если порог будет протаскиваться в обратном направлении, то возникает цепочка из межузельных атомов. Следовательно, один и тот же порог на винтовой дислокации в зависимости от направления его. протаскивания генерирует или вакансии, или межузельные атомы и соответственно называется вакансионным или межузельным порозом.

Цепочка точечных дефектов, образующихся в хвосте за про­таскиваемым порогом, быстро рассасывается диффузионным пу­тем в разные стороны, и с этой точки зрения передвижение вин­товой дислокации с порогом — необратимый процесс.

Процесс образования точечных дефектов при скольжении вин­товых дислокаций с элементарными порогами изучен недостаточно. Многие авторы придают ему большое значение, считая, что это основной механизм генерирования вакансий при пластической де­формации. Сам факт увеличения числа вакансий при пластической деформации сомнений не вызывает. В частности, именно им объяс­няется увеличение электропроводности хлористого натрия при­мерно в 100 раз после пластической деформации на 10 % (увеличение числа вакансий облегчает диффузию, а перенос электриче­ства в ионных кристаллах происходит путем диффузионного пере­мещения ионов).

Рис. 13.6 Образование цепочек вакансий при скольжении винтовой дислокации с элементарными порогами: а —дислокация с порогами до приложения напряжений; б — изгибание дислокации между порогами под действием приложен­ных напряжений; в — скользящая дислокация оставляет позади порогов цепочки вакансий: v — направление скольжения	Рис. 13.7 Образование диполя и призмати­ческих петель при скольжении винтовой дислокации с длинным порогом: v— направление скольжения

Однако до сих пор не известно число вакансий, образующихся по схеме, изображенной на рис. 13.4,6 и 13.5. Поло­жение осложняется еще и тем, что пороги могут скользить вдоль винтовой дислокации и, встречаясь, могут аннигилировать.

Образование точечных дефектов при протаскивании порогов требует затраты энергии. Пороги на дислокации затрудняют ее скольжение, и линия дислокации выгибается между порогами (ср. рис. 13.6,а и б) под действием приложенных напряжений в соответствии с формулой (11.10).

τ=αGb/r.

Когда напряжение становится больше, чем то, которое требуется для генерирования вакансий, дальнейшее выгибание линии дислокации между порогами пре­кращается, и дислокация как единое целое скользит, оставляя позади элементарных порогов цепочку вакансий (рис. 13.6,в). По-другому проявляют себя длинные пороги. При скольжении вин­товой дислокации порог сразу же отстает от нее, а так как дис­локация не может оборваться внутри кристалла, то около порога возникает петля abcd (рис. 13.7, а, б). Параллельные отрезки петли аb и cd имеют краевую ориентацию и противоположные знаки. В предельном случае, когда между этими отрезками одно межатомное расстояние, при их взаимном упругом притяжении они аннигилируют в соответствии с рис. 11.5, б и возникает цепочка вакансий. Это и есть только что рассмотренный случай протаскивания элементарного порога.

Если же на дислокации образовался длинный порог, то крае­вые дислокации аЬ и ей не аннигилируют, а стремятся вследствие упругого взаимодействия образовать в параллельных плоскостях скольжения устойчивую конфигурацию (0В на рис. 11.4,6). В ре­зультате скольжение винтовой дислокации с длинным порогом приводит к образованию довольно устойчивой петли— дислокационного диполя, состоящего из связанных длинным порогом краевых дислокаций разного знака в параллельных плоскостях скольжения (см. рис. 13.7,6). Если порог больше некоторой критиче­ской длины, то диполь не образуется, так как отрезки дислокации аb и сd могут под действием приложенных напряжений легко про­ходить один мимо другого.

Дипольная петля способна понизить свою упругую энергию, разбиваясь на вытянутые или круглые замкнутые призматические дислокационные петли (рис. 13.7,е).

Другой механизм образования дислокационных диполей—двой­ное поперечное скольжение. В плоскости поперечного скольже­ния (111) на рис. 9.18, в параллельные участки дислокаций имеют краевую ориентацию и разный знак, т. е. могут образовать устой­чивый диполь.