11.2. Силы, действующие на дислокацию

Движение дислокации вызывает пластическую деформацию кристалла, т.е. дислокация совершает работу. Учитывая это, можно оперировать представлением о действии некоторой силы на линию дислокации как на самостоятельный физический объект. Фактически же дислокация - не частица, не тело, а особая конфигурация в расположении атомов. Следовательно, ниже речь идет о силе, действующей на эту конфигурацию, и такую силу не следует смешивать с силами, действующими на атомы. Это наглядно видно из рассмотрения атомного механизма перемеще­ния винтовой дислокации на рис. 9.11. Выше уже отмечалось, что в области ядра дислокации атомы смещаются вниз и вверх в направлении действующих на них сил, а сама конфигурация называемая винтовой дислокацией, перемешается вправо перпен­дикулярно этому направлению. В рассматриваемом случае можно говорить о силе, действующей на дислокацию и направленной перпендикулярно приложенным касательным напряжениям.

В общем случае на дислокацию действуют силы разного про­исхождения: внешние силы, приложенные к поверхности кристалла, внутренние силы от действия поля напряжений вокруг соседних дислокаций, инородных атомов и других несовершенств.

Ниже рассматривается случай действия только внешних сил (внутренние напряжения от других дефектов отсутствуют). Основ­ная идея расчета состоит в следующем. Кристалл от внешнего источника получает дополнительную энергию в виде механической работы А. Вся эта энергия переходит в работу Ад, совершаемую силой Fд, действующей на дислокацию (Ад=А).

Рассмотрим краевую дислокацию на рис. 11.1 и 11.2. Однородные касательные напряжения τ от внешней силы F, совершив сквозной сдвиг верхней части кристалла относительно нижней на вели­чину b, произведут работу A=Fb. Так как касательные напря­жения действуют нa площади l₁l₂ где 1₁—длина и l₂—ширина кристалла, то сила, действующая в этой плоскости, F= τl₁l₂ и A=bτl₁l₂.

Нашей целью является вычисление силы f, действующей на единицу длины дислокации. Сила, действующая на всю дислока­цию, Fд=f l₂.

При перемещении дислокации через всю длину кристалла l₁ работа этой силы Aд=Fдl₁=f l₁l₂. Она, как уже указывалось, равна затраченной работе А.

Следовательно, fl₁l₂=bτl₁l_2.Откуда

f =bτ. (11.8)

Рис.11.1. Сдвиг, создавший краевую дислокацию А В. Стрелка — вектор сдвига (l1 и l2— длина и ширина кристалла соответственно)

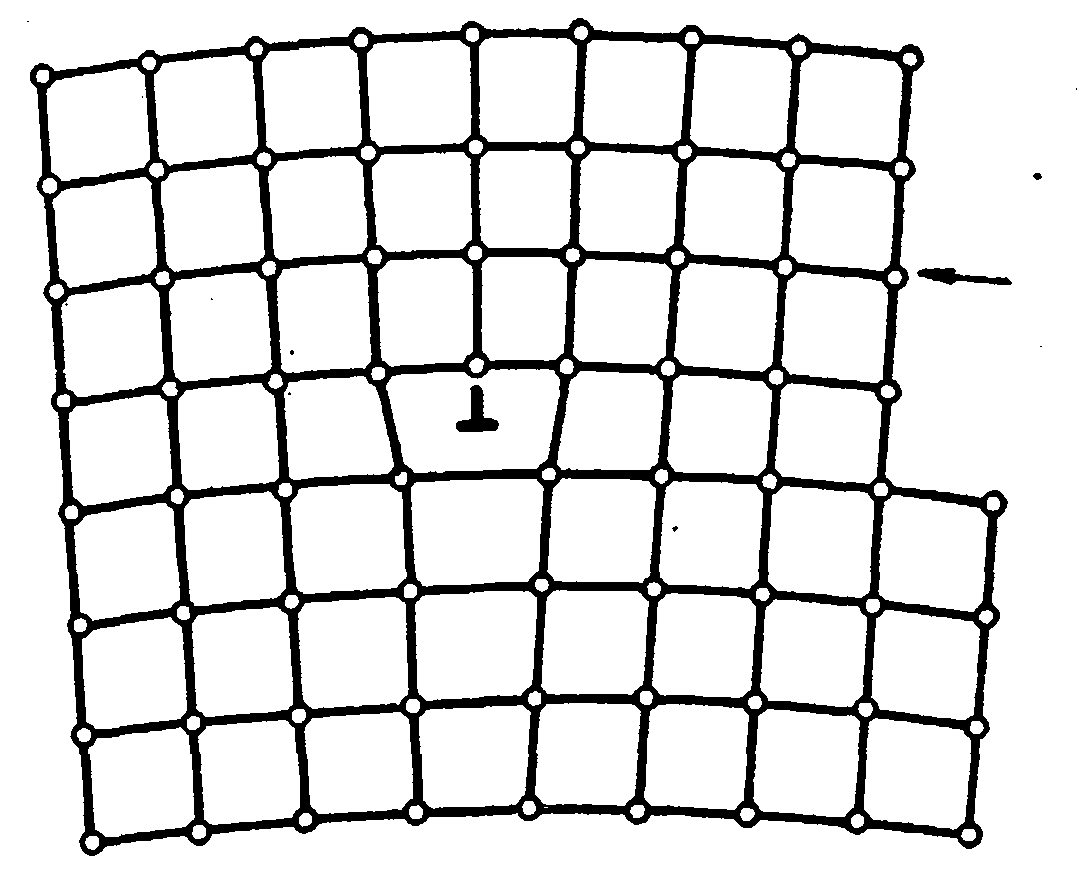
Рис. 11.2. Краевая дислокация в примитивной кубической решетке: cтрелка — вектор сдвига

Сила, действующая на единицу длины дислокации, равна про­изведению вектора Бюргерса на касательное напряжение в плос­кости скольжения. Эта сила перпендикулярна линии дислокации и направлена к той части плоскости скольжения, где скольжение еще не происходило.

Аналогичные расчеты легко выполнить для случая движения винтовой дислокации под действием однородных касательных напряжений . Здесь на сквозной сдвиг величиной b ,через всю ширину кристалла l₂ затрачивается работа внешних сил А=Fb=bτl₁l_2. На линию винтовой дислокации действует пер­пендикулярная ей сила Fд=f l₁. Работа этой силы при продвижении дислокации через всю ширину кристалла Ад=Fдl_1. Так как А=Ад, то fl₁l₂=l₁l₂ и f=b.

Доказывается, что и в случае смешанной дислокации сила, действующая на единицу ее длины, равна произведению вектора. Бюргерса на касательное напряжение и направлена перпендику­лярно линии дислокации в любой ее точке в сторону участка плоскости скольжения, еще не охваченного сдвигом. Так как вектор Бюргерса является инвариантом дислокации, а при однородных касательных напряжениях величина τ на всей плоскости скольжения одна и та же, то сила, действующая на единицу длины дислокации, по своей величине (но не по направлению) одна и та же в любом участке криволинейной дислокации, нахо­дящейся в плоскости скольжения.

Если направление приложенных касательных напряжений не совпадает с направлением вектора Бюргерса, то в формуле (11.8) величина τ представляет собой проекцию касательного напряже­ния на направление вектора Бюргерса.

Когда разные участки дислокации лежат в не параллельных плоскостях, то проекция касательного напряжения на направле­ние вектора Бюргерса в разных плоскостях может быть неодина­ковой и соответственно разной будет сила f.

Например, сила, действующая на единицу длины дислокации в плоскости (111), в общем случае должна отли­чаться от силы, действующей в плоскости (111).

Весьма важно выгибание линии дислокации под действием касательных напряжений. Выгибанию дислокации препятствует ее линейное натяжение. Найдем напряжение τ, необходимое для выгибания линии дислокации в дугу с радиусом r (рис. 11.3).

Рис. 11.3. Схема к расчету напряжения, выгибаю­щего дислокацию в дугу

На элемент дуги δl действует сила от внешних напряжений bτδl, направленная вдоль ОА. Противодействующая ей восстанав­ливающая сила F (результат линейного натяжения) направлена к центру кривизны вдоль АО. Силу F можно определить, считая, что линейное натяжение создается силами Т, приложенными по концам дуги. Тогда F = 2Tsin ¹/₂.

При малых углах sin¹/₂δθ≈¹/₂δθ и F=T δθ. Так как δθ=δl/r, то F=Tδl/r. Подставляя сюда значение Т из выражения (3), получаем для восстанавливающей силы

F=αGb²δl/r. (11.9)

Для стабильной дуги bτδ1 = F, т. е. bτδl =αGb²δl/r. Отсюда напряжение, необходимое для изгиба линии дислокации в дугу с радиусом r:

τ=αGb/r. (11.10)