9.3.Переползание краевой дислокации

При перемещении по нормали к плоскости скольже­ния краевая дислокация попадает в новые атомные плоскости, параллельные той, в которой она ранее находилась. Механизм такого перемещения, называемого переползанием, принципиально отличается от механизма скольжения. Рассмотрим перемещение положительной краевой дислокации, показанной на рис. 9.2, из своей плоскости скольжения в выше­лежащую соседнюю плоскость. Для этого необходимо, чтобы цепочка атомов на самой кромке экстраплоскости отделилась от экстраплоскости и ушла в глубь кристалла. Такое «растворение» кромки экстраплоскости (положительное переползание) является диффузионным процессом. Здесь возможны два варианта: 1) при подходе вакансий к краевой дислокации атомы с кромки экстраплоскоскости перемещаются в соседние вакантные места и 2) атомы с кромки переходят в соседние междоузлия и диффундируют от .дислокации. Первый вариант более вероятен, если учесть, что в металле часто появляется избыточная концентрация вакансии (в результате закалки, пластической деформации), а энергия образования межузельных атомов относительно велика.

Перемещение положительной дислокации вниз в соседнюю плоскость скольжения означает, что к краю экстраплоскости при­соединился один атомный ряд. Такая достройка экстраплоскости (отрицательное переползание) может проходить двумя путями: 1) присоединением межузельных атомов, диффундирующих к дислокации, и 2) присоединением соседних атомов, находящихся в регулярных положениях, с одновременным образованием вакан­сий, которые затем мигрируют в глубь кристалла.

Таким образом, перемещение краевой дислокации по нормали к своей плоскости скольжения осуществляется путем диффузион­ного перемещения атомов (к дислокации или от нее), и именно этим оно принципиально отличается от скользящего движения дислокации. В отличие от скольжения — консервативного движения, не связанного с переносом массы, переползание — неконсервативное движение происходит путем переноса массы.

Диффузия—термически активируемый процесс, и, следовательно, переползание также термически активируемый процесс, скорость которого сильно зависит от температуры. В то время как скольжение дислокации легко протекает при любых темпера­турах (вплоть до абсолютного нуля), переползание происходит с заметной скоростью лишь при сравнительно высоких темпе­ратурах.

Скорость переползания зависит не только от температуры, но и от концентрации точечных дефектов, направленное перемеще­ние которых, по существу, и обеспечивает акт переползания.

Переползание дислокации вызывает деформацию кристаллов. Когда атомы уходят с кромки экстраплоскости, происходит местное сжатие, а когда «осаждаются» на этой кромке,— местное растяжение кристалла. «Прорастание» экстраплоскости внутрь кристалла (перемещение положительной дислокации вниз или отрицательной вверх) приводит к изгибу кристалла. Приложенные сжимающие напряжения стремятся уменьшить экстраплоскость, а растягивающие способствуют ее росту.

Выше рассматривались идеализированные случаи отделения цепочки атомов вдоль всей кромки экстраплоскости или присоеди­нения ряда атомов к экстраплоскости одновременно по всей ее длине, в результате чего дислокация целиком и одновременно переползает в соседнюю параллельную плоскость скольжения. В действительности же перенос массы к кромке экстраплоскости или от нее происходит путем миграции отдельных вакансий (межузельных атомов) или небольших их комплексов, и дислока­ция переползает в новую плоскость скольжения не одновременно по всей своей длине, а по частям. Например, когда комплекс вакансий «осядет» на кромке экстраплоскости, здесь образуются две ступеньки (пороги) на дислокации. Такой процесс образования порогов — термически активируе­мый. Так как дислокация со ступеньками обладает большей энтропией, то определенное число ступенек соответствует мини­муму свободной энергии системы (при большей внутренней энергии).

В условиях термодинамического равновесия при данной тем­пературе Т число порогов на единице длины дислокации

п = п₀ exp (-Eп/kT), (9.4)

где Eп —энергия образования порога (1 эВ для порога высотой в одно межатомное расстояние); п₀ — число атомов на единице длины дислокации.

Переползание дислокации состоит в зарождении порогов и дви­жении их вдоль линии дислокации. Когда, например, к образовав­шемуся порогу присоединяется вакансия, порог смещается вдоль кромки экстраплоскости.

Энергия активации переползания

Е=Е_П+Е_Д , (9.5)

где Ед—энергия активации самодиффузии.

Если на дислокации уже имеется большое число порогов, например, в результате пересечения с другими дислокациями, то Е = Ед.

9.4. Винтовая дислокация

Понятие о винтовой дислокации в физику твердого тела ввел в 1939 г. Бюргерс.

Рис. 9.8. Сдвиг, создавший винтовую дислокацию: а — кристалл до сдвига надрезан по ABCD; б — кристалл после сдвига; ABCD — зона сдвига

Сделаем в кристалле надрез по плоскости ABCD (рис. 9.8, а) и сдвинем правую (переднюю) часть кристалла вниз на один период решетки (рис. 9.8, б). Образовавшаяся при таком сдвиге ступенька на верхней грани не проходит через всю ширину кри­сталла, оканчиваясь в точке b. Простая кубическая решетка в рассматриваемом случае выглядит так, как показано на рис. 9.9. У переднего края кристалла (вблизи точки А) сдвиг произошел ровно на один период решетки так, что верхняя атомная плос­кость справа от точки А сливается в единое целое со второй сверху плоскостью слева от точки А. Так как надрез ABCD дошел только до середины кристалла, то правая часть кристалла не может целиком сдвинуться по отношению к левой на один период решетки. Величина смещения правой части по отношению к левой уменьшается по направлению от точки А к точке В.

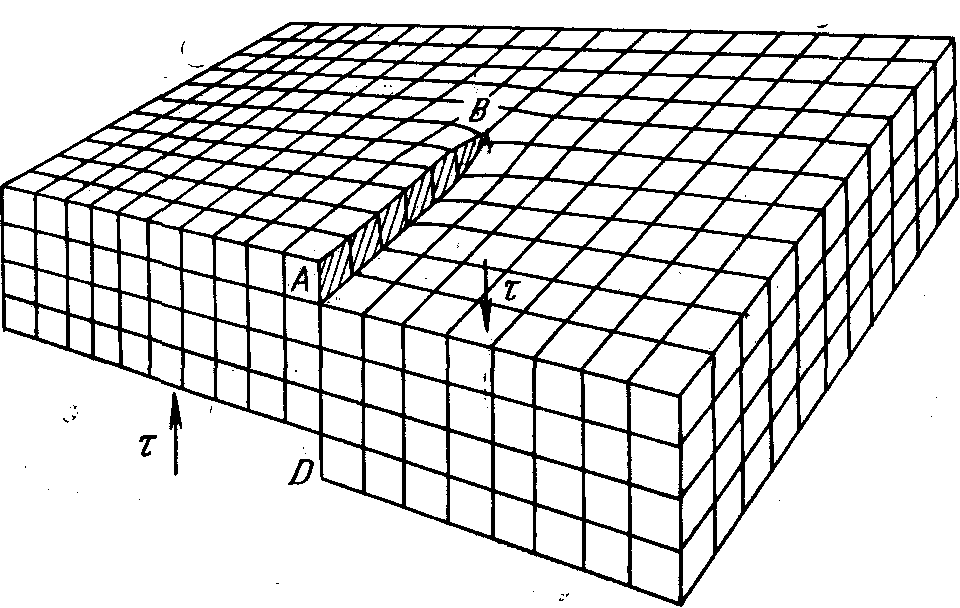
Рис. 9.9. Кристалл с винтовой дислокацией, представляющий со­бой атомную плоскость, закрученную в виде геликоида

Верхняя атомная плоскость оказывается изогнутой (см. рис. 9.9). Точно так же деформируется вторая сверху атомная плоскость; правая часть ее у передней грани кристалла смещается на один период решетки и сливается в единое целое с третьей сверху атомной плоскостью. Эта плоскость в своей правой части смещается вниз и сливается с четвертой сверху плоскостью и т. д. Если до сдвига кристалл состоял из параллельных горизонтальных атомных слоев, то после несквозного сдвига по плоскости ABCD он превратился в одну атомную плоскость, закрученную в виде геликоида (винтовой лестницы).

На рис. 9.10, а показано расположение атомов в двух вертикаль­ных плоскостях, проходящих непосредственно по обе стороны от плоскости сдвига ABCD на рис. 9.9. Если смотреть на них со стороны правой грани кристалла, то черные кружки обозначают атомы на вертикальной плоскости слева от плоскости сдвига, а светлые кружки — атомы на вертикальной плоскости справа от плоскости сдвига. Заштрихована образовавшаяся при сдвиге ступенька на верхней грани кристалла. На рис. 9.10, а плоскость скольжения ABCD совпадает с плоскостью чертежа; атомы, обозначенные черными кружками, находятся под плоскостью чертежа, а обозначенные светлыми кружками — над ней. Стрелка, направ­ленная сверху вниз, обозначает сдвигающие напряжения, прило­женные к той части кристалла, которая находится над плоскостью чертежа на рис 9.10, а, т. е. правее плоскости ABCD на рис. 9.8,б и 9.9. Стрелка, направленная снизу вверх, обозначает сдвигающие напряжения, приложенные к той части кристалла, которая нахо­дится под плоскостью чертежа на рис 9.10, а, т. е. левее плоскости ABCD на рис 9.8,б, и 9.9.

Правее линии ВС (рис 9.8,6), между атомными рядами 9 и 14 (рис. 9.10, а), положения белых и черных кружков совпа­дают, т. е. соответствующие атомы находятся на одном горизонте. Та же картина наблюдается на некотором расстоянии слева от линии ВС, между атомными рядами 1 и 5. Вокруг же линии ВС, между атомными рядами 5 и 9, атомы, обозначенные черными и белыми кружками, т. е. находящиеся под плоскостью чертежа и над ней, образуют винтовую лестницу.

Рис. 9.10 Расположение атомов в области винтовой дислокации

Таким образом, после рассмотренного сдвига по плоскости ABCD вдали от линии ВС решетка остается совершенной, а вблизи от линии ВС вдоль нее тянется область несовершенства. В одном измерении—вдоль линии ВС область несовершенства имеет макроскопический размер, а в двух других она очень мала (ее размеры по нормали к линии ВС составляют несколько периодов решетки—четыре на рис 9.10, а). Следовательно, при сдвиге по плоскости ABCD вокруг линии ВС возникло линейное несовер­шенство. Сама линия ВС представляет собой границу зоны сдвига внутри кристалла, отделяющую ту часть плоскости скольжения, где сдвиг уже прошел, от той части, где сдвиг еще не начинался. Следовательно, по определению, несовершенная область вокруг линии ВС является дислокацией. Так как после появления такой дислокации в кристалле он состоит из атомной плоскости, закрученной в винтовую лестницу, то эта дислокация называется винтовой.

Точное расположение атомов в ядре винтовой дислокации неизвестно. Схематично можно себе представить, что оно близко к расположению их по винтовой линии (рис 9.10, а и 6).

Дислокация, как и резьба винта, может быть правой или левой. На рис. 9.8 и 9.9 изображены кристаллы с правой винтовой дислокацией: линию дислокации от верхнего горизонта к нижнему следует обходить по часовой стрелке. Если же на рис 9.8, а сдвинуть вниз по плоскости ABCD левую часть кристалла, то образуется левая винтовая дислокация ВС, которую обойти по спирали с верхнего горизонта на нижний можно только против часовой стрелки. Правая дислокация превращается в левую (и наоборот) зеркальным отражением.

В отличие от краевой дислокации, которая всегда перпендикулярна вектору сдвига, винтовая дислокация параллельна вектору сдвига (сравните рис. 9.8, рис 9.9 ).

Другое принципиальное отличие винтовой дислокации от краевой состоит в следующем. Краевая дислокация в определенной кристаллографической плоскости может быть образована сдвигом только по этой плоскости. Винтовая же дислокация может образоваться при сдвиге по любой кристаллографической плоскости, содержащей линию дислокации, по любой поверхности, оканчивающейся на этой линии. Если на рис. 9.8, а сделать надрез по плоскости, находящейся под любым углом к ABCD, но так, чтобы этот надрез оканчивался в кристалле на линии ВС, то после сдвига мы получим ту же винтовую дислокацию ВС. Таким образом, винтовая дислокация в отличие от краевой не опреде­ляет однозначно плоскость сдвига.

9.5. Скольжение винтовой дислокации

Схема атомного механизма перемещения винтовой дислокации показана на рис.9.11. Расположение атомов, соединенных сплошными линиями на рис.9.11, а, такое же, как и на рис.9.10,а.

Плоскость скольжения ABCD совпадает с плоскостью чертежа, черные кружки обозначают атомы под плоскостью чертежа, а белые — над ней Верхняя стрелка обозначает сдвигающие напря­жения, действующие на ту часть кристалла, которая находится над плоскостью чертежа, а нижняя стрелка — напряжения, дейст­вующие на часть кристалла под этой плоскостью. Заштрихована ступенька, возникшая при сдвиге на верхней грани кристалла (рис. 9.9). Область несовершенства, внутри которой атомы образуют винтовую лестницу, находится между атомными ря­дами 5 и 7.

Пунктирные линии соединяют атомы после перемещения (скольжения) винтовой дислокации на один период решетки вправо. Если в исходном положении область несовершенства находилась между атомными рядами 5 и 7, то после смещения на один период решетки вправо она находится между атомными рядами 6 и 8.

Рис. 9.11. Смещения атомов при скольжении узкой (а) и широкой (б) винтовой дислокации слева направо на одно межатомное расстояние

Атомы над плоскостью чертежа (белые кружки) под действием сдвигающих напряжений, обозначенных верхней стрелкой, смещаются вниз. Атомы под плоскостью чертежа (чер­ные кружки) под действием сдвигающих напряжений, обозначен­ных нижней стрелкой, смещаются вверх. Необходимо обратить внимание на три важных обстоятельства. Во-первых, дислокация перемещается на один период решетки вправо в результате пере­движений атомов только внутри области несовершенства; атомы вне области несовершенства остаются на своих местах. Во-вторых, дислокация перемещается на один период решетки вслед­ствие передвижения атомов внутри ядра дислокации всего лишь на доли периода решетки. В этом отношении скольжение винто­вой дислокации аналогично скольжению краевой дислокации. В-третьих, в области ядра винтовой дислокации атомы смещаются в направлении действующих на них сил (вниз и вверх на рис. 11), а сама дислокация перемещается перпендикулярно этому направ­лению (вправо на рис. 9.11). Последнее отличает винтовую дисло­кацию от краевой; при скольжении краевой дислокации экстра­плоскость изменяет свое положение в направлении действующих касательных напряжений.

Перемещение винтовой дислокации увеличило площадь сту­пеньки и площадь зоны сдвига. В исходном состоянии на рис. 9.11 зона сдвига, т. е. часть плоскости скольжения, где сдвиг уже совершился, находится между атомными рядами 1 и 5, а после перемещения дислокации вправо на один период решетки зона сдвига находится между атомными рядами 1 и 6. При продвиже­нии винтовой дислокации слева направо на рис. 9.11 область сдвига постепенно распространяется на всю ширину кристалла.

Как видно на рис.9.12, под действием одинаковых сдвигающих напряжений винтовые дислокации разного знака скользят в прямо противоположных направлениях.

Винтовая дислокация не определяет однозначно плоскость сдвига. Действительно, вокруг линии ВС на рис. 9.8, 9.10 наблюдается цилиндрическая симметрия искажения решетки. Схемы атомного строения в области дисло­кации, аналогичные изображенным на рис. 9.10, а и 9.11, справедливы не только для плоскостей, параллельных ABCD (рис. 9.8, б), но и для любых вертикальных плоскостей, проходящих через линию ВС на рис. 9.8, б. Соответственно схема перемещений атомов на рис. 9.11, обеспечивающих скольжение винтовой дислокации, также справедлива для любых плоскостей, проходящих через линию ВС на рис. 9.8, б. Винтовая дислокация в принципе может скользить в любой кристаллографической, плоскости, кото­рая содержит линию дислокации и вектор сдвига.

В отличие от краевой винтовая дислокация может переходить из одной атомной плоскости в другую без переноса массы — скольжением. Если на пути движения винтовой дислокации в плоскости Р встречается какой-то барьер , то дисло­кация начинает скользить в другой атомной плоскости R, нахо­дящейся под углом к первоначальной плоскости скольжения Р (рис. 9.13). Этот процесс называют поперечным скольжением.

Рис. 9.12. Кристалл с правой (П) и левой (Л) винтовыми дислокация­ми, скользящими в плоскости ABCD: VП и VЛ ---направления скольжения правой и левой дислокаций под дей ствием напряжений τ

Рис. 9.13. Двойное поперечное скольжение винтовой дислокации ВС

Пройдя некоторый путь в плоскости поперечного скольжения и удалившись от барьера, винтовая дислокация может перейти в атомную плоскость S, параллельную первоначальной плоскости скольжения Р. Этот процесс называют двойным поперечным скольжением. Многократное его повторение называют множест­венным поперечным скольжением. Например, в г. ц. к. решетке винтовая дислокация, скользившая в плоскости (111), легко пере­ходит в плоскость поперечного скольжения (111), затем вновь скользит в одной из параллельных плоскостей (111), снова совер­шает поперечное скольжение по плоскости (111) и т. д.

Кроме барьеров, одна из причин поперечного скольжения - изменение вектора приложенных напряжений.

В отличие от краевой, винтовая дислокация не может пере­мещаться с помощью диффузионного механизма.