7.1 Координационное число, координационный полиэдр, число формульных единиц

Зная модель кристаллической структуры, т. е. пространственное рас­положение атомов относительно элементов симметрии в элементарной ячейке — их координаты, а, следовательно, и характеристики правильных систем точек, которые занимают атомы, можно сделать ряд кристаллохимических выводов, используя достаточно простые приемы описания струк­тур. Поскольку 14 выведенных решеток Браве не могут отразить все многообразие известных к настоящему времени кристаллических струк­тур, необходимы характеристики, позволяющие однозначно описать ин­дивидуальные особенности каждой кристаллической структуры. К таким характеристикам, дающим представление о геометрическом характере структуры, относятся: координационные числа (КЧ), координационные многогранники (КМ), или полиэдры (КП), и число формульных единиц (Z). Прежде всего по модели можно решить вопрос о типе химической формулы рассматриваемого соединения, т. е. установить количественное соотношение атомов в структуре. Это нетрудно сделать на основе ана­лиза взаимного окружения — взаимной координации — атомов разных (или одинаковых) элементов.

Термин «координация атома» был введен в химии в конце XIX в. в процессе формирования ее новой области — химии координационных (комплексных) соединений. И уже в 1893 г. А. Вернер ввел понятие коор­динационное число (КЧ) как число атомов (лигандов - ионы, непосредственно связанные с центральными атомами (катионами)), непосредствен­но связанных с центральным. Химики в свое время столкнулись с тем фактом, что число связей, образуемых атомом, может отличаться от его формальной валентности и даже превышать ее. Например, в ионном со­единении NaCl каждый ион окружен шестью ионами противоположного заряда (KЧ_Na/Cl = 6, KЧ_Cl/Na = 6), хотя формальная валентность атомов Na и С1 равна 1. Таким образом, согласно современному представлению, КЧ — это число ближайших к данному атому (иону) соседних атомов (ионов) в структуре кристалла независимо от того, являются они атомами того же сорта, что и центральный, или иного. При этом межатомные расстоя­ния являются основным критерием, используемым при подсчете КЧ.

Например, в кубических структурах модификации a-Fe (рис. 7.2.а) и CsCl (рис. 7.2. в) координационные числа всех атомов равны 8: в струк­туре a-Fe атомы Fe располагаются в узлах объемноцентрированного куба, отсюда KЧ_Fe= 8; в структуре CsCl в вершинах элементарной ячейки располагаются ионы Сl^- , а в центре объема — ион Cs⁺, координационное число которого тоже равно 8 (КЧ _Cs/Cl = 8), так же как и каждый ион Cl окружен восемью ионами Cs⁺ по кубу (КЧ _Cl/Cs = 8). Это подтверждает от­ношение Cs : С1 = 1: 1 в структуре этого соединения.

а	б	в
Рис. 7.2. Кристаллические структуры α-Fe (а и б) и CsCl (в).

В структуре α –Fe координационное число атома Fe по первой координационной сфере равно 8, с учетом второй сферы — 14 (8 + 6). Координационные полиэдры — соответственно куб и ромбододекаэдр.

Координационные числа и координационные многогранники являются важнейшими характеристиками конкретной кристаллической структуры, отличающими ее от остальных структур. На этой основе можно проводить классификацию, относя конкретную кристаллическую структуру к определенному структурному типу.

Установить тип химической формулы по структурным данным (т. е. по модели структуры или по ее проекции — чертежу) можно и иным пу­тем, подсчитав число атомов каждого сорта (химического элемента), при­ходящихся на одну элементарную ячейку. Это подтверждает тип химической формулы NaCl.

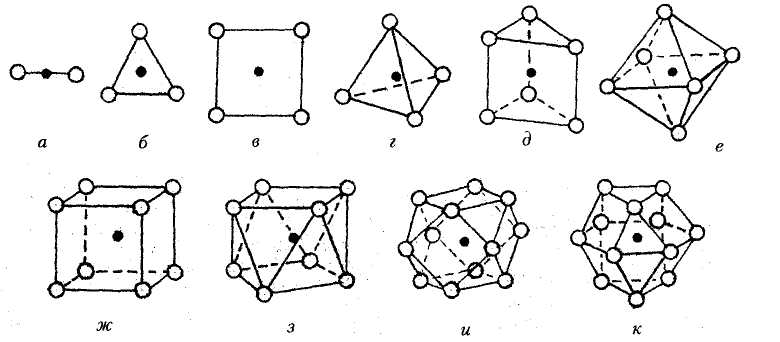
Рис. 7.3. Некоторые координационные полиэдры, встречающиеся в кристаллических структурах: а - гантель (КЧ = 2); б - треугольник (КЧ = 3); в - квадрат (КЧ = 4); г - тетраэдр (КЧ = 4); д - тригональная призма (КЧ = 6); е - октаэдр (КЧ = 6);ж — куб (КЧ = 8); з — томсоновский куб (КЧ = 8); и — архимедов кубооктаэдр (КЧ = 12); к — гексагональный аналог кубооктаэдра (КЧ =12)

В структуре NаС1 (рис. 7.4), типичной для ионных кристаллов типа АВ (где А—атомы (ионы) одного сорта, В—другого), в построении элементарной ячейки принимают участие 27 атомов обоих сортов, из них 14 атомов А (шары большого размера) и 13 атомов В (меньшие шары), но полностью входит в ячейку лишь один. атом, находящийся в ее центре. Атом, находящийся в центре грани элементарной ячейки, принадлежит одновременно двум ячейкам—данной и смежной с ней. Поэтому данной ячейке принадлежит лишь половина этого атома. В каждой из вершин ячейки сходится одновременно по 8 ячеек, поэтому данной ячейке принадлежит лишь 1/8 атома, расположенного в вершине. От каждого атома, находящегося на ребре ячейки, ей принадлежит лишь 1/4.

Вычислим общее число атомов, приходящихся на одну элементарную ячейку NаС1:

Положение атома	Объем входящих в ячейку	Число атомов	Всего в ячейку приходится
В вершине В середине ребра В центре грани В центре ячейки	1/8 1/4 1/2 1	8 12 6 1	1 3 3 1

Итак, на долю ячейки, показанной на рис. 7.4, приходится не 27 атомов, а всего 8 атомов: 4 атома натрия и 4 атома хлора.

- Cl - Na

Рис.7.4 Структура каменной соли

Определение числа атомов в ячейке Браве позволяет кроме типа хи­мической формулы получить еще одну полезную константу — число фор­мульных единиц, обозначаемое буквой Z. Для простых веществ, состоящих из атомов одного элемента (Сu, Fe, Se и др.), число формульных единиц соответствует числу атомов в элементарной ячейке. Для простых молеку­лярных веществ (I₂, S₈ и т. д.) и молекулярных соединений (СО₂) число Z paвно числу молекул в ячейке. В подавляющем же боль­шинстве неорганических и интерметаллических соединений (NaCl, CaF₂, СuАu и т. д.) молекул нет, и в этом случае вместо термина «количество молекул» используют термин «число формульных единиц».

Число формульных единиц можно определить экспериментально в процессе рентгеновского исследования вещества.